1)Макросистемы: примеры, особенности, состояния макросистем и способы исследования макросистем. Средние величины по времени, по ансамблю, эргодическая гипотеза.

Системой называют ограниченную область пространства, в которой находятся объекты исследования. Макросистема – система содержащая огромное количество частиц или объектов. 1 см³ газа 2.7*10¹⁹ частиц (Газ – макросистема) Равновесное состояние – состояние когда макро параметры не меняются с течением времени. Неравновесные меняются. Виды макросистем: газ, идеальный газ, плазма, жидкость, твердое тело, жидкие кристаллические тела. Состояния макросистемы:1)равновесное,2)неравновесное. Способы исследования Равновесное 1-молекулярно кинетический, 2-термодинамический. Неравновесное 1-физическая кинетика(явление переноса - диффузия, вязкость, теплопроводность, 2-синергетика(для систем которых длительное время находится в равновесном состоянии не переходя в неравновесное.

2)Уравнение состояния идеального газа – уравнение Менделеева-Клапейрона. Смесь идеальных газов, закон Дальтона. Изопроцессы. Идеальный газ – пример макросистемы, в которой размеры частиц намного меньше, чем расстояния до других частиц, отсутствует взаимодействие м/д частицами и столкновения частиц друг с другом и стенками сосудов абсолютно упруги.

Э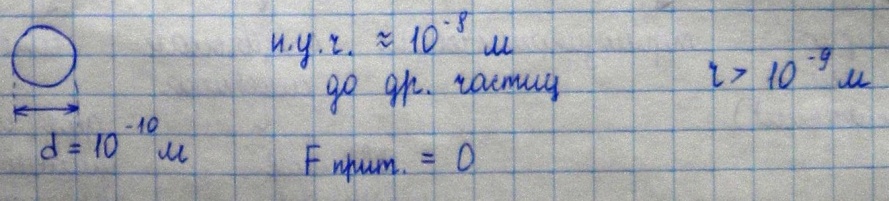 та форма записи носит имя уравнения (закона) Менделеева — Клапейрона. В случае постоянной массы газа уравнение можно записать в виде:

 — давление,  — молярный объём,  — абсолютная температура,К  — универсальная газовая постоянная.

З акон Дальтона: Закон о суммарном давлении смеси газов. Давление смеси химически не взаимодействующих идеальных газов равно сумме парциальных давлений

Закон о растворимости компонентов газовой смеси

П ри постоянной температуре растворимость в данной жидкости каждой из компонентов газовой смеси, находящейся над жидкостью, пропорциональна их парциальному давлению.

И зопроцессы. Изопроцессы — термодинамические процессы, во время которых масса и ещё одна из физических величин — параметров состояния: давление, объём или температура — остаётся неизменной. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический, энтропии — адиабатический.. Линии, изображающие данные процессы на какой-либо термодинамической диаграмме, называются изобара, изохора , изотерма и адиабата соответственно. Изопроцессы являются частными случаями политропного процесса.

3) Основные уравнения молекулярно-кинетической теории идеального газа. Вывод уравнения Клаузиуса и основного уравнения молекулярно-кинетической теории идеального газа. Основное уравнение мкт

где k является постоянной Больцмана - отношением газовой постоянной R к числу Авогадро, а i - число степеней свободы молекул. Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) газовой системы с микроскопическими (масса молекул, средняя скорость их движения).ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ. Молекулярно-кинетическая теория - теория, объясняющая тепловые явления в макроскопических телах и свойства этих тел на основе их молекулярного строения. Основные положения молекулярно-кинетической теории:1) вещество состоит из частиц - молекул и атомов, разделенных промежутками, 2)эти частицы хаотически движутся, 3)частицы взаимодействуют друг с другом. МАССА И РАЗМЕРЫ МОЛЕКУЛ Массы молекул и атомов очень малы. Например, масса одной молекулы водорода равна примерно 3,34*10 ^-27 кг, кислорода - 5,32*10 ^-26 кг. Масса одного атома углерода m_0C=1,995*10 ^-26 кг Относительной молекулярной (или атомной) массой в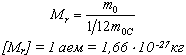 ещества Mr называют отношение массы молекулы (или атома) данного вещества к 1/12 массы атома углерода:(атомная единица массы).

Количество вещества - это отношение числа молекул N в данном теле к числу атомов в 0,012 кг углерода N_A:

Моль - количество вещества, содержащего столько молекул, сколько содержится атомов в 0,012 кг углерода. Число молекул или атомов в 1 моле вещества называют постоянной Авогадро:

М олярная масса - масса 1 моля вещества:

Молярная и относительная молекулярная массы вещества связаны соотношением: М = М_r*10 ^-3 кг/моль.

О сновное уравнение молекулярно-кинетической теории можно записать в виде

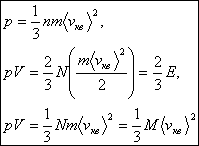  - основное уравнение молекулярно-кинетической теории идеальных газов, где  – средняя квадратичная скорость молекул, E - суммарная кинетическая энергия поступательного движения всех молекул газа, n - концентрация молекул, m - масса одной молекулы, M=Nm - масса газа, N - число молекул в объеме газа V.

4)Температура - мера кинетической энергии молекул. Средняя кинетическая энергия молекул. Средняя квадратичная скорость молекул. Скорость называют средней квадратичной скоростью

С редняя кинетическая энергия хаотического движения молекул газа пропорциональна абсолютной температуре:

Средняя квадратичная скорость молекул

С равнивая уравнение состояния идеального газа и основное уравнение кинетической теории газов, записанные для одного моля (для этого число молекул N возьмём равным числу Авогадро N_А), найдём среднюю кинетическую энергию одной молекулы:

О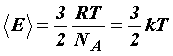 ткуда

.           (31)

Средняя кинетическая энергия поступательного движения молекулы не зависит от её природы и пропорциональна абсолютной температуре газа T. Отсюда следует, что абсолютная температура является мерой средней кинетической энергии молекул.

Величина R/N_А = k в уравнении (31) получила название постоянной Больцмана и представляет собой газовую постоянную, отнесенную к одной молекуле:  k = 1,38·10^-23 Дж/К^-23.

Так как 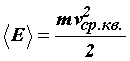= kТ, то средняя квадратичная скорость равна

.  (32) Подставляя значение средней кинетической энергии поступательного движения молекул (31) в основное уравнение молекулярно–кинетической теории газов, получим другую форму уравнения состояния идеального газа:

P = n₀kT.           (33)

Давление газа пропорционально произведению числа молекул в единице объема на его термодинамическую температуру.

Молекулярно-кинетическая теория позволяет определить абсолютную температуру идеального газа через среднюю энергию^[4] совокупности частиц системы. Из основного уравнения молекулярно-кинетической теории:^[5]

п олучается, что абсолютная температура пропорциональна средней энергии:

где i — число степеней свободы молекул газа; k — постоянная Больцмана; T -абсолютная температура;  — средняя энергия,  — энергия каждого j-того атома в случае одноатомного идеального газа. E_k может быть разной для разных атомов, поэтому нельзя говорить о температуре одного атома

5)Степени свободы. Закон Больцмана о равнораспределении молекул по степеням свободы движения молекул. Числом степени свободы – называют числом независимых координат, с помощью которых можно определить положение тела в пространстве. Жесткая связь молекул предполагает 1)поступательное движение, 2) вращательное движение. Упругая связь предполагает 1) поступательное движение, 2) вращательное, 3) колебательное. i= i_пост+i_вращ+i_колеб

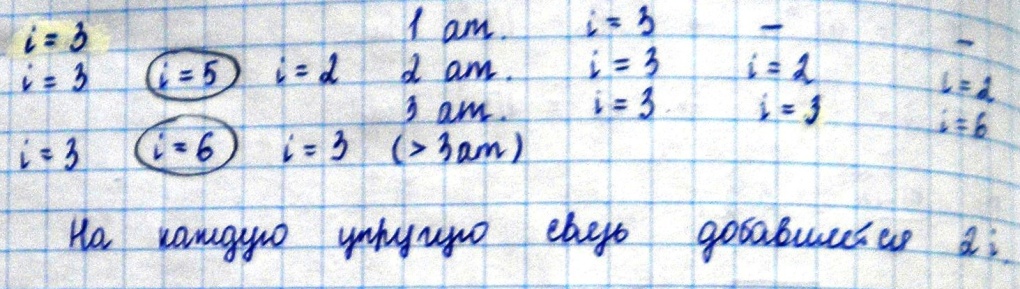
Теорема Больцмана На каждую степень свободы поступательного и вращательного движения среднем приходится одинаковая энергия, равная 1/2KT (дописать в ручную)