Запись тонкой голограммы.
Далее будем рассматривать идеи связанные с записью тонкой голограммы [17].
Схема записи тонкой голограммы приведена на рис.1.2.
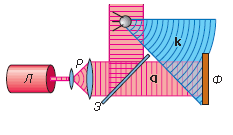
Рис.1.2. Схема записи тонкой голограммы.
Л- лазер, Р – расширитель светового пучка, З – полупрозрачное зеркало, Ф – фотопластинка, q – опорная волна, k – рассеянная объектом предметная волна.
Излучение лазера через полупрозрачное зеркало направляется на фотопластинку. Соответствующая ему волна носит название опорной и может приближенно считаться плоской монохроматической:
(1.6)
Отраженная полупрозрачным зеркалом часть излучения лазера используется для освещения голографируемого объекта. Рассеянный его атомами свет так же оказывается монохроматическим и описывается предметной волной, которая уже не может рассматриваться как плоская. Фронт и амплитуда предметной волны могут иметь весьма сложные пространственные конфигурации, в которых содержится полная информация обо всех оптических свойствах голографируемого объекта. Воздействие такой волны на органы зрения с последующей переработкой сигналов нервной системой и мозгом в конечном итоге приводят к возникновению в сознании зрительного образа. Очевидно, что для возникновения зрительного ощущения, тождественного создаваемому реальным объектом, достаточно с максимальной точностью воспроизвести электромагнитное поле предметной волны.
Для удобства анализа голографического метода записи и восстановления предметной волны представим ее в виде суперпозиции плоских волн:
(1.7)
и рассмотрим процесс записи каждой пространственной гармоники в отдельности. При сложении двух плоских монохроматических волн одинаковой частоты в пространстве возникает волна с периодически меняющейся амплитудой, бегущая вдоль биссектрисы образованного волновыми векторами qи kугла между ними (Рис.1.3).
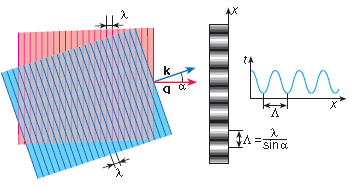
Рис.1.3. Сложение двух плоских монохроматических волн одинаковой частоты в пространстве и возникающая волна с периодически меняющейся амплитудой.
При падении такой волны на фотопластинку (расположенную, например, перпендикулярно волновому вектору опорной волны) на ней возникает стационарное во времени распределение интенсивности, представляющее собой чередующиеся параллельные светлые и темные полосы. Расстояние между полосами максимальной интенсивности оказывается равным:
(1.8)
После экспонирования и обработки такой голограммы одной плоской монохроматической волны она будет представлять собой пластинку, во многом подобную классической дифракционной решетке с периодом, даваемым указанным выше соотношением. Более строгий расчет возникающей интерференционной картины позволяет найти закон изменения интенсивности света на поверхности фотопластинки. Оказывается, что возникающая дифракционная решетка имеет существенное отличие от классической: ее функция пропускания изменяется не скачками в интервале между 0 и 1, а непрерывно по косинусоидальному закону. В случае же нескольких волн с различными векторами k результирующая голограмма представляет собой достаточно сложный узор, являющейся простой суммой "косинусоидальных решеток", создаваемых каждой из записываемых волн.