95.Уравнение гармонической волны. Параметры волн.

Гармонические колебания- частный случай переодического колебания, при котором физическая величина, описывающая колебательный процесс, изменяется по гармоническому закону(закону синуса или косинуса)

Х=A*sin*(2∏tν+φ₀) или х=A*sin*(ω*t+ φ₀) или х=А*sin(2∏t/T+ φ₀)

Х=A*cos*(2∏tν+φ₀) или х=A*cos*(ω*t+ φ₀) или х=А* cos*(2∏t/T+ φ₀)

Х- смещение относительно положения равновесия

А-амплитуда колебаний-модуль максимального смещения относительно положения равновесия

φ =2∏tν+φ₀₌ ω*t+ φ₀₌2∏t/T+ φ₀ Фаза колебаний( измеряется в рад)

φ₀- Начальная фаза, t-время ν-линейная частота(Гц) T-период колебаний , ω -круговая или циклическая частота

ν=1/T= ω/2∏

Если разность фаз двух гармонических колебаний ∆ φ=2∏n ,то колебания происходят в одной фазе (синфазные), а если ∆ φ=∏+2∏n , то колебания происходят в противофазе,n- произвольное число.

Когда тело совершает гармонические колебания, то его проекция скоростиV_x ( производная по времени от смещения) и проекция ускорения a_x ( производная по времени от проекции скорости) изменяется тоже по гармоническому закону с той же частотой, что и частота изменения смещения:

V_x=xꞌ=- ωAsin(ωt+ φ₀)=V_mcos(ωt+ φ₀+∏/2)

A_x= V_xꞌ=-ω²Acos(ωt+ φ₀)=- ωV_mcos(ωt+ φ₀)=a_mcos(ωt+ φ₀₊∏)= -ω²x

9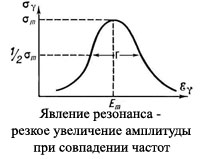 1. Резонанс. Амплитудно-частотная характеристика

Явление, которое возможно в колебательной системе, подверженное внешнему воздействию. Заключается в резком возрастании амплитуды.

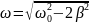, где ω0-совственная частота колебания, β-коэффицент затухания

92. автоколебания

Автоколеба́ния — незатухающие колебания в диссипативной динамической системе с нелинейной обратной связью, поддерживающиеся за счёт энергии постоянного, то есть непериодического внешнего воздействия.

S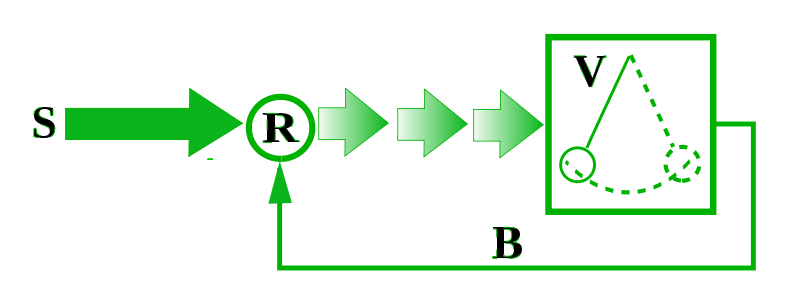 — источник постоянного (непериодического) воздействия; R — нелинейный регулятор, преобразующий постоянное воздействие в переменное (например, в прерывистое во времени), которое и «раскачивает» колеблющийся элемент (элементы) системы V, а колебания через обратную связь B управляют работой регулятора R, задавая фазу и частоту его действия. Диссипация (рассеивание энергии) в автоколебательной системе восстанавливается за счёт поступления в неё энергии из источника постоянного воздействия, благодаря чему автоколебания не затухают.

Примерами автоколебаний могут служить:

незатухающие колебания маятника часов за счёт постоянного действия тяжести заводной гири;

колебания скрипичной струны под воздействием равномерно движущегося смычка

возникновение переменного тока в цепях мультивибратора и в других электронных генераторах при постоянном напряжении питания;

колебание воздушного столба в трубе орга́на, при равномерной подаче воздуха в неё.

93 параметрические колебания. Если внешние воздействие может приводить в изменению параметров системы, то такие колебания наз параметрическими, если на ситему внешние силы не действуют, но система получает внешнюю энергию через изменение параметров.

Пример: качели, тарзанка

94 Волновой процесс – явления распространения колебаний в пространстве(переноса вещества не происходит) волны бывают:

1. Упругие(звуковые) – это волны, для распространения которых должна быть упругая среда.

2. Электромагнитные – могут распространятся в отсутствии среды. Происходит колебания электрического и магнитного векторов. Продольные - колебания среды происходят вдоль направления распространения волн,при этом возникают области сжатия и разрежения среды. Поперечные - колебания среды происходят перпендикулярно направлению их распространения,

при этом происходит сдвиг слоев среды. возникают только в твердых телах.