
- •Математическая модель. Классификация и принципы построения математических моделей. Примеры задач, решаемых методами математического программирования.
- •Постановка и различные формы записи задач линейного программирования. Множество допустимых решений. Оптимальное решение задачи линейного программирования.
- •Стандартная и каноническая формы представления задач линейного программирования.
- •Геометрическая интерпретация задач линейного программирования. Многогранник решений. Алгоритм решения задачи линейного программирования графическим методом.
- •Геометрический смысл симплекс-метода решения задач линейного программирования. Построение начального опорного плана.
- •Симплекс-метод. Критерий оптимальности опорного плана.
- •Симплекс-метод. Правило перехода к новому опорному плану.
- •Симплекс-таблица. Пересчет симплекс-таблиц. Алгоритм симплекс-метода решения задач линейного программирования.
- •Метод искусственного базиса.
- •Экономическая интерпретация двойственных задач планирования производства.
- •Двойственная задача линейного программирования и алгоритм её формирования.
- •Формулировка теоремы двойственности. Нахождение оптимального плана двойственной задачи.
- •Анализ модели на устойчивость по отношению к изменениям запасов продукции (основная теорема).
- •Экономическая и математическая формулировки транспортной задачи.
- •Закрытая и открытая модели транспортной задачи. Приведение открытой транспортной задачи к закрытой.
- •Методы построения начального опорного плана транспортной задачи: метод северо-западного угла и метод минимального элемента.
- •Вырожденные и невырожденные планы транспортной задачи. Система потенциалов, экономический смысл. Критерий оптимальности опорного плана транспортной задачи.
- •Получение оптимального плана транспортной задачи с помощью метода потенциалов.
- •Алгоритм улучшения плана транспортной задачи. Понятие цикла, пересчет по циклу. Снятие вырожденности плана.
- •Транспортные задачи с ограничениями на пропускную способность сети.
- •Матричные игры. Платежная матрица. Игра с нулевой суммой.
- •Принцип минимакса и максимина. Верхняя и нижняя цена игры.
- •Оптимальные стратегии игроков. Решение матричной игры с седловой точкой.
- •Чистые и смешанные стратегии игроков. Вероятностная интерпретация. Теорема о существовании решения игры в смешанных стратегиях (теорема о минимаксе).
- •Графическое решение в случае игры 2 m и n2 .
- •Сведение решения игры в произвольном случае к задаче линейного программирования.
- •Математические модели межотраслевого баланса. Матрицы прямых и полных производственных затрат.
- •Валовой, конечный и чистый продукты. Определение цены конечной продукции.
- •Определение себестоимости продукции.
Математические модели межотраслевого баланса. Матрицы прямых и полных производственных затрат.
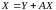 .
.
Это уравнение называется уравнением межотраслевого баланса.
Валовой, конечный и чистый продукты. Определение цены конечной продукции.
валовой продукт = конечный продукт + внутрипроизводственное потребление
Чистый продукт отрасли есть ее валовой продукт минус то количество продукции, которое было затрачено на производство этого валового продукта во всех отраслях:
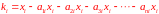 ,
,
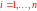 .
.
Определение себестоимости продукции.
Рассмотрим
механизм образования себестоимости
продукции.
Предположим, что для производства одной
единицы (валовой) продукции
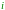 –й
отрасли необходимо затратить
–й
отрасли необходимо затратить
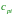 единиц
единиц
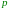 –го
сырья,
–го
сырья,
 .
Сырье понимается в широком смысле
слова: закупаемые материалы, электроэнергия,
производственные фонды, труд и т.д.
.
Сырье понимается в широком смысле
слова: закупаемые материалы, электроэнергия,
производственные фонды, труд и т.д.
Обозначим
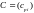 —
—
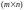 ‑матрицу
удельных коэффициентов прямых затрат
сырья. Тогда полные затраты
‑матрицу
удельных коэффициентов прямых затрат
сырья. Тогда полные затраты
 –го
вида сырья, необходимые для производства
валового продукта
–го
вида сырья, необходимые для производства
валового продукта
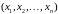 ,
равны
,
равны
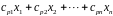 .
.
Следовательно,
полные затраты всех видов сырья,
необходимого на выполнение производственного
задания, есть вектор
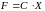 .
.
Определим
затраты сырья в пересчете на 1 единицу
конечной продукции
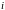 –й
отрасли. С учетом соотношения
–й
отрасли. С учетом соотношения
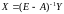 получаем
получаем
 .
.
Таким
образом, матрица
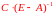 есть
матрица коэффициентов полных затрат
сырья.
есть
матрица коэффициентов полных затрат
сырья.
Если
известен вектор цен за одну единицу
сырья каждого вида,
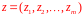 ,
то полные затраты на производство
конечного продукта
,
то полные затраты на производство
конечного продукта
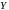 равны
равны
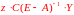 ,
а себестоимость производства одной
единицы продукции
,
а себестоимость производства одной
единицы продукции
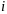 й
отрасли равна
й
отрасли равна
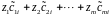 ,
где
,
где

элемент матрицы
элемент матрицы
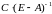 ,
стоящий в
,
стоящий в
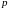 й
строке,
й
строке,
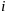 м
столбце.
м
столбце.
