Содержание
1.Метод половинного деления………………………………………..2
1.1.Теория метода половинного деления...........................................2
1.2.Постановка задачи………………………………………………..3
1.3.Решение задачи…………………………………………………..3-4
2.Метод итерации……………………………………………………….4
2.1.Теория метода итерации…………………………………….......4
2.2.Постановка задачи………………………………………………..5
2.3.Решение задачи…………………………………………………..5-6
3. Геометрическая интерпретация метода итерации……………....6
3.1.Теория геометрической интерпретации метода итерации…..6
3.2.Постановка задачи…………………………………………………7
3.3.Решение задачи……………………………………………………7-8
4. Метод Ньютона(метод касательных)………………………………8
4.1.Теория метода Ньютона………………………………………...8-9
4.2.Постановка задачи………………………………………………….9
4.3.Решение задачи……………………………………………………9-10
Вывод………………………………………………………………………11
1.Метод половинного деления
1.1.Теория метода половинного деления
Пусть
дана функция
,
где
-
корень
предполагаемого уравнения,
.
Процедура уточнения положения корня
заключается в последовательно вложенные
друг в друга отрезков, каждый из которых
содержит корень уравнения. Для этого
находим:
k=0,1,2,3,…
Следующий
интервал выбираем тот, на котором функция
имеет
разные знаки.
y
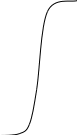f(b0)
f(c1)
a0
x
c2 c1 b0
f(a0)
Процесс
завершается, когда длина текущего
интервала неопределенности становится
меньше
,
задающий точность нахождения корня. В
качестве приближенного значения корня
берется середина последнего интервала
неопределенности
.
Методика решения задачи
1.Найти
интервал неопределенности
,
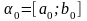задать
и
положить k=0
2.Найти
3.
Если
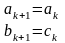
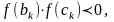то
то
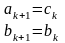
4.
Если
1.2.Постановка задачи
Решить
уравнение
методом
половинного деления с точностью до
0,001.
1.3.Решение задачи
=0.001;
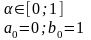
Строим таблицу:
a |
b |
c |
f(a) |
f(b) |
f© |
abs|b-a| |
конец |
0 |
1 |
0,5 |
0,100335 |
-0,19134 |
0,161055 |
1 |
нет |
0,5 |
1 |
0,75 |
0,161055 |
-0,19134 |
0,030153 |
0,5 |
нет |
0,75 |
1 |
0,875 |
0,030153 |
-0,19134 |
-0,07042 |
0,25 |
нет |
0,75 |
0,875 |
0,8125 |
0,030153 |
-0,07042 |
-0,01742 |
0,125 |
нет |
0,75 |
0,8125 |
0,78125 |
0,030153 |
-0,01742 |
0,007062 |
0,0625 |
нет |
0,78125 |
0,8125 |
0,796875 |
0,007062 |
-0,01742 |
-0,00501 |
0,03125 |
нет |
0,78125 |
0,796875 |
0,789063 |
0,007062 |
-0,00501 |
0,00107 |
0,015625 |
нет |
0,7890625 |
0,796875 |
0,792969 |
0,00107 |
-0,00501 |
-0,00196 |
0,007813 |
нет |
0,7890625 |
0,792969 |
0,791016 |
0,00107 |
-0,00196 |
-0,00044 |
0,003906 |
нет |
0,7890625 |
0,791016 |
0,790039 |
0,00107 |
-0,00044 |
0,000315 |
0,001953 |
нет |
0,790039063 |
0,791016 |
0,790527 |
0,000315 |
-0,00044 |
-6,3E-05 |
0,000977 |
да |
Ответ:
2.Метод итерации
2.1.Теория метода итерации
Пусть
известно, что корень уравнения
лежит
на отрезке
.
Методика решения задачи
1.Приводим
уравнение
к виду
.
Для сходимости метода необходимо
обеспечить выполнение условия
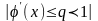(q-некоторая
const).
При
этом задача сводится к нахождению
абсциссы точки пересечения прямой
.
2.
Задать начальное приближение
и
.
3.
Вычислить следующее приближение
.
4.
Если
итерации завершаются и
,
если
,
k=k+1,
и переходим в п.3.
2.2.Постановка задачи
Решить уравнение методом итерации с точностью до 0,001.
2.3.Решение задачи
=0.001;
Проверяем
условие сходимости:
.
Условие сходимости выполняется, т.к.,
Строим таблицу:
xk |
xk+1 |
|xk+1-xk| |
конец |
1 |
0,899256 |
0,100744 |
НЕТ |
0,899256012 |
0,846333 |
0,052923 |
НЕТ |
0,846333005 |
0,819037 |
0,027296 |
НЕТ |
0,819036606 |
0,805049 |
0,013988 |
НЕТ |
0,805049094 |
0,7979 |
0,00715 |
НЕТ |
0,797899505 |
0,794249 |
0,003651 |
НЕТ |
0,794248968 |
0,792386 |
0,001863 |
НЕТ |
0,792385939 |
0,791435 |
0,000951 |
ДА |
3. Геометрическая интерпретация метода итерации
3.1.Теория геометрической интерпретации метода итерации
Методика решения задачи
1.можно
заменить уравнение
на
,
где с –const.
2.
заменяем на
,
,
.
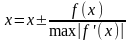При
этом знак выбирают так, чтобы выполнилось
.
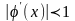3.можно выразить так, чтобы для получения уравнения выполнилось условие сходимости: в окрестности искомого корня.
3.2.Постановка задачи
Решить
уравнение
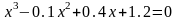с
использованием геометрической
интерпретации метода итерации с
точностью до 0,001.
3.3.Решение задачи
,
Находим значение производной в точках 0 и -1:
Выбираем
максимальное значение, т.е.,
.
Выбираем знак «-», чтобы выполнилось условие сходимости:
Проверяем
условие сходимости:
Строим таблицу:
xk |
xk+1 |
|xk+1-xk |
конец |
0 |
-0,33333333 |
0,333333333 |
нет |
-0,33333 |
-0,61625514 |
0,282921811 |
нет |
-0,61626 |
-0,80555665 |
0,189301511 |
нет |
-0,80556 |
-0,88615169 |
0,080595037 |
нет |
-0,88615 |
-0,90591533 |
0,019763637 |
нет |
-0,90592 |
-0,90927552 |
0,003360189 |
нет |
-0,90928 |
-0,90978635 |
0,000510832 |
да |
