21. Методика изучения числовых последовательностей и прогрессий.

Числовую последовательность {a_n}, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом d, называют арифметической прогрессией. Число d называется разностью арифметической прогрессии:

a_n + 1 = a_n + d.

Так как a_n – 1 = a_n – d, то a_n + 1 + a_n – 1 = 2a_n. Верно и обратное.

Последовательность {a_n} является арифметической тогда и только тогда, когда для любого n > 1 выполняется рекуррентное соотношение

Формула общего члена арифметической прогрессии {a_n} такова: a_n = a₁ + (n – 1) · d.

Доказательство

Докажем это пользуясь методом математической индукции. Легко убедиться, что для n = 1 данная формула верна. Пусть эта формула верна для n = k. Докажем ее справедливость для n = k + 1. Имеем a_k + 1 = a_k + d = a₁ + (k – 1) · d + d = a₁ + k · d. Теорема доказана.

 Сумма n первых членов арифметической прогрессии {a_n} равна

  Геометрическая прогрессия

Числовую последовательность {b_n}, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число q <> 0, называют геометрической прогрессией:

b_n + 1 = b_n · q. Важно отметить, что число q, которое называется знаменателем прогрессии, отлично от нуля. Так как   то  Верна и обратная теорема.

Последовательность {b_n} является геометрической тогда и только тогда, когда для любого n > 1 выполняется соотношение где при всех n. Тем не менее, важно понимать, что формула справедлива только для геометрической прогрессии с положительными членами, а предыдущее соотношение верно для произвольной геометрической прогрессии. Каждый член геометрической прогрессии {b_n} определяется формулой b_n = b₁ · q^n – 1.

Доказательство

Докажем это пользуясь методом математической индукции. Легко убедиться, что при n = 1 данная формула верна. Пусть эта формула верна для n = k. Докажем ее справедливость для n = k + 1. Имеем b_k + 1 = b_k · q = b₁ · q^k – 1 · q = b₁ · q^k. Теорема доказана.

Сумма n первых членов геометрической прогрессии {b_n} равна

при q <> 1 и S_n = n · b₁ при q = 1. Эти формулы также доказываются методом математической индукции.

При |q| < 1 , поэтому в этом случае геометрическая прогрессия называется бесконечно убывающей. Суммой бесконечно убывающей геометрической прогрессии называется число , где S_n – сумма n первых членов геометрической прогрессии.

Сумма бесконечно убывающей геометрической прогрессии (|q|  <  1) равна Для доказательства достаточно заметить, что 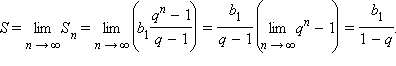В предпоследнем переходе использовались свойства пределов последовательностей.

21. Методика введения и изучения понятия производной в средней школе.

Различные подходы к введению производной определяются логической связью этого понятия с более общим понятием предела функции в точке. Логический подход при введении производной в качестве базисного понятия использует определение предела функции в точке. Так в учебных программах по математике 1968 года, используя этот подход, определяли это понятие: 1) исходя из арифметического толкования предела функции (определение по Коши или на языке абсолютной погрешности): 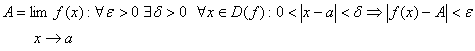2) исходя из операции предела функции в точке через окрестности (топологическое):  a- предельная точка множества E, т.е. 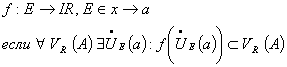В действующих школьных программах по математике при введении производной функции используют исторический подход, т.е. первоначально формируются понятия производной, и только затем, как обобщение, понятие предела функции. При таком подходе большое внимание уделяется практическим аспектам изучения производной.