
- •1.1 Предмет, цели и задачи методики преподавания математики и ее связи с другими науками.
- •1.2.Математика как учебный предмет в школе.
- •1.3 Психолого-педагогические основы обучения математики.
- •1.4 Воспитание учащихся в процессе обучения математике. Развитие познавательного интереса школьников при обучении математике.
- •1.6. Проблема интеграции школьного курса математики и пути её решения.
- •1.7 Дидактические принципы обучения школьников математике.
- •1.8 Развивающее обучение. Принципы развивающего обучения.
- •1.9 Общие дидактические методы обучения школьников математике. Классификация методов обучения.
- •1.10.Методы научного познания в обучении математике
- •1.11 Определение понятий. Классификация понятий. Возможные ошибки в определении математических понятий школьниками и работа учителя по их предупреждению.
- •1.12 Определение понятий. Виды определений. Требования к определениям. Методика изучения математических понятий в школе.
- •1.13. Математическое понятие: термин, объем, содержание. Классификация понятий. Требования к классификации. Способы образования математических понятий.
- •1.15 Структура теорем. Виды теорем. Методика изучения теорем в школьном курсе математики.
- •1.16 Сущность понятия «доказательства». Методы доказательства теорем.
- •1.17 Общие методы решения математических задач. Классификация задач. Роль алгоритмов и эвристик в обучении решению задач. Организация обучения решению математических задач.
- •1.18 Задачи в школьном курсе математики и общая методика их решения. Роль и функции задач в математике. Основные этапы в решении задачи. Общие умения по решению задач.
- •1.19 Современные формы организации обучения математике. Урок как основная форма организации учебного процесса. Типы уроков. Основные требования к современному уроку.
- •1.21 Воспитание у учащихся потребности в доказательствах теорем. Методика обучения учащихся теоремам и их доказательствам. Подготовка учителя к доказательству теорем на уроке.
- •1.22 Дифференциация в обучении школьников математике в системе основного и дополнительного образования.
- •1.23 Развитие математических способностей и воспитание учащихся в процессе математического образования.
- •1.24 Анализ урока математики. Его роль в интенсификации учебного процесса.
- •9. Выводы и предложения.
- •1.25 История развития методики преподавания математики. Основные противоречия процесса обучения математике. Актуальные проблемы методики преподавания математики.
- •2.1 Методика изучения начал систематического школьного курса планиметрии.
- •2.2 Методика изучения подобных треугольников.
- •2.3 Методика изучения основных соотношений между элементами треугольника.
- •2.4 Методика изучения понятия равенства фигур. Доказательство первых теорем планиметрии. Признаки равенства треугольников.
- •2.5 Методика изучения четырехугольников и их свойства.
- •2.6 Методика изучения величин в школьном курсе планиметрии.
- •2.7 Обобщение понятия степени в школьном курсе математики.
- •2.8 Исторические и логические последовательности изучения числовых множеств. Общий принцип расширения числовых множеств. Общая схема изучения новых чисел.
- •2.9 Методика повторения и дальнейшего изучения натуральных чисел. Изучение обыкновенных и десятичных дробей.
- •2.10 Методика изучения тригонометрических функций в курсе планиметрии.
- •2.11 Методика изучения показательной и логарифмической функций в средней школе.
- •2.12 Методика введения и изучения рациональных чисел.
- •2.13 Методика введения и изучения иррациональных чисел.
- •2.16 Методика изучения тригонометрических уравнений и неравенств в средней школе.
- •2.17 Методика изучения показательных и логарифмических уравнений и неравенств в средней школе.
- •2.18 Методика изучения уравнений и их систем в средней школе. Равносильность уравнений. Алгебраические уравнения и их системы.
- •2.19 Методика изучения неравенств и их систем в средней школе. Метод интервалов при решении неравенств.
- •2.20 Методика изучения функций. Понятие функций. Возможная методическая схема изучения функций в базовой школе. Методика изучения алгебраических функций.
- •Методика изучения числовых последовательностей и прогрессий.
- •Методика введения и изучения понятия производной в средней школе.
- •Использование свойств тригонометрических функций в курсе математики в средней школы.
- •Методика обучения школьников решению текстовых задач арифметическим методом и методом составления уравнений и неравенств.
- •I. Арифметический метод.
- •II. Алгебраический метод.
- •Методические особенности изучения тригонометрических функций в средней школе. Построение графиков тригонометрических функций.
- •2.26 Использование понятия производной в курсе алгебры средней школы.
2.13 Методика введения и изучения иррациональных чисел.
Введение начинается с целесообразно подобранной задачи. Например: извлечение квадратного корня из положительного числа, не являющегося полным квадратом; каким числом выражается длина диагонали квадрата со стороной 1; чему равна сторона квадрата, если известно, что его площадь равна 3.
Практические задачи: задачи измерения; каждой ли точке координатной прямой соответствует рац число?
Изображение чисел на координатной прямой
Покажем, что т. В’ соответствует числу, не явл рацион, т. к. диагональ квадрата ОВ несоизмерима с его стороной ОА
Д-во, что т. В не соотв. никакому рац числу
Т.
к. т. В’ находится на ОХ,
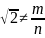
От
противного: пусть
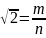 – несократимая дробь. Обе части –
неотрицательны, возведем в квадрат,
получим:
– несократимая дробь. Обе части –
неотрицательны, возведем в квадрат,
получим:
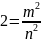 ,
,
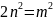 ,
=>
,
=>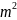 – четное, =>
– четное, =>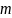 – четное. Значит
можно представить в виде
– четное. Значит
можно представить в виде
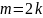 .
Подставим в
:
.
Подставим в
:
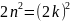 =>
=> ,
,
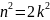 =>
=>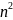 – четное,
– четное,
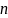 – четное. Тогда имеем
– четное. Тогда имеем
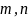 – четные. Это противоречит тому, что
– четные. Это противоречит тому, что
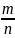 – несократимая дробь. =>
=>
– несократимая дробь. =>
=>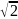 не
является рациональным числом.
не
является рациональным числом.
Таким образом, число можно изобразить на координатной прямой некоторым числом, которое не является рациональным. Такие числа называются иррациональными.
2
подход
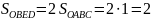
С
другой стороны
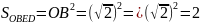 .
.
Если натуральное число не есть квадрат некоторого натурального числа, то оно есть квадрат иррационального числа. Таким образом, – иррациональное число.
3 подход
Иррациональные
числа – есть бесконечные десятичные
непериодические дроби. Так как
нельзя извлечь нацело
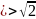 есть бесконечная десятичная непериодическая
дробь
есть число иррациональное.
есть бесконечная десятичная непериодическая
дробь
есть число иррациональное.
4 подход
Рассмотрим приближенное значение с недостатком и с избытком:
С недостатком: 1,4; 1,41; 1,414; 1,4142
С избытком: 1,5; 1,42; 1,415; 1,4143
Объединим эти последовательности: 1,4< 1,41< 1,414 <1,4142 < < 1,4143 < 1,415 < 1,42 < 1,5
Докажем, что границей или пределом последовательностей является некоторое иррациональное число.
Пусть границей явл , с другой стороны границей явл несократимая дробь .
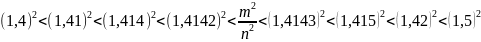
Таким
образом, на границе последовательности,
представляющей квадраты членов,
последовательности приближений с
недостатком и с избытком находится с
одной стороны число 2, а с другой -
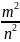 ,
причем
,
причем
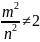 => данную последовательность определяют
два числа, не равные между собой, а это
невозможно => последовательности
определяют единственное число
.
=> данную последовательность определяют
два числа, не равные между собой, а это
невозможно => последовательности
определяют единственное число
.
Действия над иррациональными числами
1) сравнение (можно как десятичные дроби, сравнивая кол-во единиц в соответствующих разрядах, можно как квадраты корней)
2) сложение, вычитание, умножение, деление (нельзя выполнять как с десятичными дробями)
Часто иррациональные числа как бесконечные десятичные дроби заменяют их приближенными значениями, и результаты действий находят по правилам приближенных значений.
2.14 Методика изучения процентов. Основные задачи на проценты в школьном курсе математики.
Понятие процента имеет широкое практическое применение, поэтому оно является обязательной частью школьной программы по математике. Школьники должны научиться решать основные задачи на проценты, представлять их в виде десятичных и обыкновенных дробей.
Традиционно тема «Проценты» изучается в рамках младших классов среднего звена. Можно выделить несколько подходов к изучению данной темы.
Первый подход. Рассмотрение процентов ведется как отдельная тема, без опоры на дроби. Нахождение нескольких процентов от числа осуществляется в два действия. Изучение дробей ведется отдельной темой, гораздо позже задач на проценты. Таким образом, обучение идет от частного к общему, что менее эффективно и дает меньше возможностей для развития обучаемого.
Второй подход. Задачи на проценты осваиваются как частный случай задач на дроби и все приемы решения переносятся на них, то есть изучение идет от общего случая - задач на дроби, к частному. В большинстве современных учебников реализован второй подход.
Рассматриваются три основные задачи на проценты:
Задача вида К1.
Пример 1: Бригада рабочих за день отремонтировала 40% дороги, имеющей длину 120 м. Сколько метров дороги было отремонтировано бригадой за день?
Решение:
120 м составляет 100%
1) 120:100 =1,2 м составляет 1%.
2) м отремонтировано бригадой за день.
Ответ: За день бригада отремонтировала 48 м дороги.
Задача вида К2.
Пример 2: Ученик прочитал 72 страницы, что составляет 30% числа всех страниц книги. Сколько страниц в книге?
Решение:
Неизвестное число - 100%.
1) 72:30=2,4 страницы составляет 1%.
2) страниц составляет 100%.
Ответ: В книге 240 страниц.
Задача вида П1.
Пример 3: В классе из 40 учащихся 32 правильно решили задачу. Сколько процентов учащихся правильно решили задачу?
Решение:
40 учащихся составляют 100%.
1) 40:100=0,4 составляет 1%.
2) 32:0,4=80; 32 ученика составляют 80%.
Ответ: 80% учащихся правильно решили задачу.
Методика изучения тождественных преобразований.
Процесс формирования навыков тождественных преобразований выражений достаточно сложный и требует от учителя большой и кропотливой работы. В этом процессе можно выделить три основных этапа:
1) запоминание алгоритма учащимися и его непосредственное применение;
2) применение нового алгоритма в совокупности с другими ранее известными алгоритмами преобразований;
3) решение широкого круга задач с использованием нового алгоритма.
Поясним на примере изучения формулы сокращенного умножения разности двух выражений на их сумму.
1-й
этап - запоминание формулы
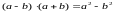 и соответствующей ей словесной
формулировки, а так же непосредственное
применение этой формулы к упрощению
таких выражений как
и соответствующей ей словесной
формулировки, а так же непосредственное
применение этой формулы к упрощению
таких выражений как
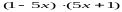 .
.
На этом этапе необходимо добиваться от учащихся понимания того, что результат преобразования выражения не зависит от порядка сомножителей в произведении и от порядка слагаемых в сумме, а определяется разностью выражений.
2-й
этап состоит в формировании умения
применять формулу
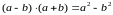 в
сочетании с другими тождественными
преобразованиями. Это прежде всего
касаться применения изученной формулы
параллельно с использованием свойств
степенней с натуральным показателем.
в
сочетании с другими тождественными
преобразованиями. Это прежде всего
касаться применения изученной формулы
параллельно с использованием свойств
степенней с натуральным показателем.
Например,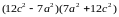 .
.
Более высокая ступень сформированности навыка на 2-м этапе связана с умением применять изученную формулу в сочетание со сложением, вычитанием и умножением многочленов, с другими формулами сокращенного умножения.
3-й
этап формирования навыка выполнения
преобразований по формуле
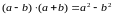 сводится к выработке умения применять
новую формулу при решении уравнений,
неравенств и их систем, при исследовании
функций, в задачах на делимость и т.д.
Например, доказать, что
сводится к выработке умения применять
новую формулу при решении уравнений,
неравенств и их систем, при исследовании
функций, в задачах на делимость и т.д.
Например, доказать, что
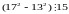 .
.
Каждый этап формирования навыков тождественных преобразований выражений имеет свою специфику и связан с определенными методическими трудностями.
