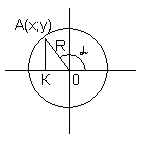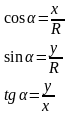- •1.1 Предмет, цели и задачи методики преподавания математики и ее связи с другими науками.
- •1.2.Математика как учебный предмет в школе.
- •1.3 Психолого-педагогические основы обучения математики.
- •1.4 Воспитание учащихся в процессе обучения математике. Развитие познавательного интереса школьников при обучении математике.
- •1.6. Проблема интеграции школьного курса математики и пути её решения.
- •1.7 Дидактические принципы обучения школьников математике.
- •1.8 Развивающее обучение. Принципы развивающего обучения.
- •1.9 Общие дидактические методы обучения школьников математике. Классификация методов обучения.
- •1.10.Методы научного познания в обучении математике
- •1.11 Определение понятий. Классификация понятий. Возможные ошибки в определении математических понятий школьниками и работа учителя по их предупреждению.
- •1.12 Определение понятий. Виды определений. Требования к определениям. Методика изучения математических понятий в школе.
- •1.13. Математическое понятие: термин, объем, содержание. Классификация понятий. Требования к классификации. Способы образования математических понятий.
- •1.15 Структура теорем. Виды теорем. Методика изучения теорем в школьном курсе математики.
- •1.16 Сущность понятия «доказательства». Методы доказательства теорем.
- •1.17 Общие методы решения математических задач. Классификация задач. Роль алгоритмов и эвристик в обучении решению задач. Организация обучения решению математических задач.
- •1.18 Задачи в школьном курсе математики и общая методика их решения. Роль и функции задач в математике. Основные этапы в решении задачи. Общие умения по решению задач.
- •1.19 Современные формы организации обучения математике. Урок как основная форма организации учебного процесса. Типы уроков. Основные требования к современному уроку.
- •1.21 Воспитание у учащихся потребности в доказательствах теорем. Методика обучения учащихся теоремам и их доказательствам. Подготовка учителя к доказательству теорем на уроке.
- •1.22 Дифференциация в обучении школьников математике в системе основного и дополнительного образования.
- •1.23 Развитие математических способностей и воспитание учащихся в процессе математического образования.
- •1.24 Анализ урока математики. Его роль в интенсификации учебного процесса.
- •9. Выводы и предложения.
- •1.25 История развития методики преподавания математики. Основные противоречия процесса обучения математике. Актуальные проблемы методики преподавания математики.
- •2.1 Методика изучения начал систематического школьного курса планиметрии.
- •2.2 Методика изучения подобных треугольников.
- •2.3 Методика изучения основных соотношений между элементами треугольника.
- •2.4 Методика изучения понятия равенства фигур. Доказательство первых теорем планиметрии. Признаки равенства треугольников.
- •2.5 Методика изучения четырехугольников и их свойства.
- •2.6 Методика изучения величин в школьном курсе планиметрии.
- •2.7 Обобщение понятия степени в школьном курсе математики.
- •2.8 Исторические и логические последовательности изучения числовых множеств. Общий принцип расширения числовых множеств. Общая схема изучения новых чисел.
- •2.9 Методика повторения и дальнейшего изучения натуральных чисел. Изучение обыкновенных и десятичных дробей.
- •2.10 Методика изучения тригонометрических функций в курсе планиметрии.
- •2.11 Методика изучения показательной и логарифмической функций в средней школе.
- •2.12 Методика введения и изучения рациональных чисел.
- •2.13 Методика введения и изучения иррациональных чисел.
- •2.16 Методика изучения тригонометрических уравнений и неравенств в средней школе.
- •2.17 Методика изучения показательных и логарифмических уравнений и неравенств в средней школе.
- •2.18 Методика изучения уравнений и их систем в средней школе. Равносильность уравнений. Алгебраические уравнения и их системы.
- •2.19 Методика изучения неравенств и их систем в средней школе. Метод интервалов при решении неравенств.
- •2.20 Методика изучения функций. Понятие функций. Возможная методическая схема изучения функций в базовой школе. Методика изучения алгебраических функций.
- •Методика изучения числовых последовательностей и прогрессий.
- •Методика введения и изучения понятия производной в средней школе.
- •Использование свойств тригонометрических функций в курсе математики в средней школы.
- •Методика обучения школьников решению текстовых задач арифметическим методом и методом составления уравнений и неравенств.
- •I. Арифметический метод.
- •II. Алгебраический метод.
- •Методические особенности изучения тригонометрических функций в средней школе. Построение графиков тригонометрических функций.
- •2.26 Использование понятия производной в курсе алгебры средней школы.
2.10 Методика изучения тригонометрических функций в курсе планиметрии.
Триг. ф-ции служат для описания разнообр. периодич. процессов: восход/заход, прилив/отлив
Триг. ф-ции – первые трансцендентные ф-ции, изуч. в школе. Роль и место их опр-тся след. факторами: ) Тр. ф-ции представляют собой замечательный вычислительный аппарат для решения задач в планиметрии и стереометрии. ) Учения о тр. ф-циях позволяют наглядно и убедительно продемонстрировать важнейшие св-ва ф-ций вообще.Впервые знакомство происходит в 8 кл. (геометрия), где реализуется первый способ введения: ч/з стороны в прямоуг. треугольнике. В 8 кл. второй способ: ч/з координаты радиус-вектора. По Атанасяну в 9 кл. третий способ: ч/з единичную окружность (следствие 2-го способа).
Возможные пути введения тр. ф-ций:
. Ч/з ст-ны прямоуг. треугольника. Осн. недостаток: затруднение при переходе к углам > 90 и переходе к тригон. ф-циям числового аргумента.
. Ч/з тригонометрические линии в круге.
. Следствие способа: ч/з проекции единичного вектора, т.е. sin и cos – это новые названия ординаты и абсциссы точки единичной окр-сти, полученной в рез-те поворота начального радиуса ОА на угол относительно (0;0). Поэтому рассм-тся угол поворота. Рассм-тся радианные и градусные измерения углов.
Т.обр., каждому допустимому углу соотв. единств. зн-ние sin, cos…, кот. наз. тригоном. ф-циями угла. Из этого следует
V способ: определение триг. ф-ции как ф-ции угла.
В 7-9 кл. св-ва триг. ф-ций выводятся на основании их опр-ний как функций угла поворота начального радиуса в триг. окружности (периодичность, знаки по четвертям, знакопостоянство, четность, монотонность, D(y), E(y). Т.обр., роль триг. круга в иссл-нии триг. ф-ций очень велика. Св-ва, вывед. в 7-9 кл., использ. в решении задач вычислительного характера.
В 10 кл.: знакомство с формулами приведения (мнемоническое правило: формулы приведения позволяют перейти от ф-ции тупого угла к ф-ции острого); осн. триг. тождества, ф-лы сложения, ф-лы двойного угла; построение гафиков триг. ф-ций. И графики и круг примен. для решения триг. уравнений и неравенств. В рез-те изучения дети должны уметь преобразовывать триг. выражения, строить графики.
Завершается изучение триг. функций общей схемой исследования функций на примере исследования триг.ф-ции (14 свойств – обл. определения, обл. значений, четность, наименьший положительный период, к-ты точек пересечения графика с осью Ох, к-ты точек пересечения графика с осью Оy, промежутки, на которых f принимает положительные значения, промежутки, на которых f принимает отрицательные значения, промежутки возрастания, промежутки убывания, точки минимума, минимумы ф-ции, точки максимума, максимумы ф-ции)
Как д-ть, что наименьший положительный период для sin явл. 2π?
Период
– это Т≠0,
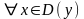
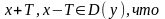 f(x)=f(x+T)=f(x-T).
f(x)=f(x+T)=f(x-T).
2π≠0,
x+2π,
x-2π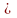 D(y),
что sin(x)=sin(x+2π)=sin(x-2π)
D(y),
что sin(x)=sin(x+2π)=sin(x-2π)
2π≠0, x+2π, x-2π D(y), что cos(x)=cos(x+2π)=cos(x-2π) □
2.11 Методика изучения показательной и логарифмической функций в средней школе.
Ознакомление учащихся с показательной и логарифмической функциями начиная с изучения свойств степеней и логарифмов.
Курс
алгебры знакомит учащихся с понятием
степени с рациональным показателем.
Таким образом для любого основания
степени
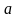 (где
(где
 ,
,
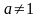 )
можно построить функцию:
)
можно построить функцию:
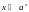 ,
,
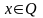 ,
область определения которой – множество
действительных чисел. Необходимо ввести
определение степени с иррациональным
показателем. Используемое свойство
степени с основным, например, большим
единицы (возрастании), рациональное
приближение иррационального числа α:
r1<
α< r2.
Исходя из графического изображения
зависимости показателя степени и
значения степени, показывается, что
найдется такое значение y,
которое будет наибольшим среди всех
ar1
и наименьшим среди всех ar2
, которое можно считать значением aα.
,
область определения которой – множество
действительных чисел. Необходимо ввести
определение степени с иррациональным
показателем. Используемое свойство
степени с основным, например, большим
единицы (возрастании), рациональное
приближение иррационального числа α:
r1<
α< r2.
Исходя из графического изображения
зависимости показателя степени и
значения степени, показывается, что
найдется такое значение y,
которое будет наибольшим среди всех
ar1
и наименьшим среди всех ar2
, которое можно считать значением aα.
Затем формируется определение показательной функции: функция, заданная формулой y=ax( , ), называется показательной функцией с основанием a, и формулируемые основные свойства: D(ax)=R; E(ax)=RТ; ax возрастает при a>1 и ax убывает при 0<a<1; напоминаются основные свойства степеней. Т.о. показательная функция есть систематизация, обобщение и расширение знаний учащихся о свойствах степени.
Логарифмическая функция – новый математический объект для учащихся. К понятию логарифма учащихся подводят в процессе решения показательного уравнения ax=b в том случае, если b нельзя представить в виде степени с основанием a. Наше уравнение в случае b>0 имеет единственный корень, который называют логарифмом b по основанию a и обозначают logab, т.е. alogab=b. Одновременно с введением нового понятия учащиеся знакомятся с основным Логарифмическим тождеством. При работе с логарифмами применяются следующие их свойства, вытекающие из свойств показательной функции:
При любом ( ) и любых положительных x и y, выполнены равенства:
1. loga1=0
2. logaa=1
3. logaxy= logax+ logay
4. logax/y= logax- logay
5. logaxp= plogax
Изучение
логарифмической функции начинается с
выделения определения: функцию, заданную
формулой
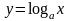 называют логарифмической функцией с
основанием
.
Основные свойства выводится из свойств
показательной функции:
называют логарифмической функцией с
основанием
.
Основные свойства выводится из свойств
показательной функции:
1.
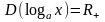 ,
,
2.
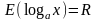 ,
,
3. Логарифмическая функция на всей области определения возрастает (при a>1) или убывает (при 0<a<1).
Покажем,
что
при a>1
возрастает. Пусть
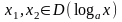 и
и
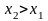 ,
надо доказать, что:
,
надо доказать, что:
 .
Допустим противное, т.е. что
.
Допустим противное, т.е. что
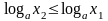 .
Т.к. показательная функция
.
Т.к. показательная функция
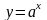 при a>1
возрастает, то из неравенства
следует:
при a>1
возрастает, то из неравенства
следует:
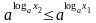
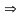
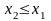 ,
что противоречит выбору
,
что противоречит выбору
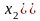 .
Следовательно:
и функция
при a>1
– возрастает.
.
Следовательно:
и функция
при a>1
– возрастает.
Т.к. при a>1 функция возрастает, то логарифмическая функция положительна при x>1 и отрицательна для 0<x<1 (для основания 0<a<1 – наоборот). На основании рассмотренных свойств строится график этой функции.