
- •1.1 Предмет, цели и задачи методики преподавания математики и ее связи с другими науками.
- •1.2.Математика как учебный предмет в школе.
- •1.3 Психолого-педагогические основы обучения математики.
- •1.4 Воспитание учащихся в процессе обучения математике. Развитие познавательного интереса школьников при обучении математике.
- •1.6. Проблема интеграции школьного курса математики и пути её решения.
- •1.7 Дидактические принципы обучения школьников математике.
- •1.8 Развивающее обучение. Принципы развивающего обучения.
- •1.9 Общие дидактические методы обучения школьников математике. Классификация методов обучения.
- •1.10.Методы научного познания в обучении математике
- •1.11 Определение понятий. Классификация понятий. Возможные ошибки в определении математических понятий школьниками и работа учителя по их предупреждению.
- •1.12 Определение понятий. Виды определений. Требования к определениям. Методика изучения математических понятий в школе.
- •1.13. Математическое понятие: термин, объем, содержание. Классификация понятий. Требования к классификации. Способы образования математических понятий.
- •1.15 Структура теорем. Виды теорем. Методика изучения теорем в школьном курсе математики.
- •1.16 Сущность понятия «доказательства». Методы доказательства теорем.
- •1.17 Общие методы решения математических задач. Классификация задач. Роль алгоритмов и эвристик в обучении решению задач. Организация обучения решению математических задач.
- •1.18 Задачи в школьном курсе математики и общая методика их решения. Роль и функции задач в математике. Основные этапы в решении задачи. Общие умения по решению задач.
- •1.19 Современные формы организации обучения математике. Урок как основная форма организации учебного процесса. Типы уроков. Основные требования к современному уроку.
- •1.21 Воспитание у учащихся потребности в доказательствах теорем. Методика обучения учащихся теоремам и их доказательствам. Подготовка учителя к доказательству теорем на уроке.
- •1.22 Дифференциация в обучении школьников математике в системе основного и дополнительного образования.
- •1.23 Развитие математических способностей и воспитание учащихся в процессе математического образования.
- •1.24 Анализ урока математики. Его роль в интенсификации учебного процесса.
- •9. Выводы и предложения.
- •1.25 История развития методики преподавания математики. Основные противоречия процесса обучения математике. Актуальные проблемы методики преподавания математики.
- •2.1 Методика изучения начал систематического школьного курса планиметрии.
- •2.2 Методика изучения подобных треугольников.
- •2.3 Методика изучения основных соотношений между элементами треугольника.
- •2.4 Методика изучения понятия равенства фигур. Доказательство первых теорем планиметрии. Признаки равенства треугольников.
- •2.5 Методика изучения четырехугольников и их свойства.
- •2.6 Методика изучения величин в школьном курсе планиметрии.
- •2.7 Обобщение понятия степени в школьном курсе математики.
- •2.8 Исторические и логические последовательности изучения числовых множеств. Общий принцип расширения числовых множеств. Общая схема изучения новых чисел.
- •2.9 Методика повторения и дальнейшего изучения натуральных чисел. Изучение обыкновенных и десятичных дробей.
- •2.10 Методика изучения тригонометрических функций в курсе планиметрии.
- •2.11 Методика изучения показательной и логарифмической функций в средней школе.
- •2.12 Методика введения и изучения рациональных чисел.
- •2.13 Методика введения и изучения иррациональных чисел.
- •2.16 Методика изучения тригонометрических уравнений и неравенств в средней школе.
- •2.17 Методика изучения показательных и логарифмических уравнений и неравенств в средней школе.
- •2.18 Методика изучения уравнений и их систем в средней школе. Равносильность уравнений. Алгебраические уравнения и их системы.
- •2.19 Методика изучения неравенств и их систем в средней школе. Метод интервалов при решении неравенств.
- •2.20 Методика изучения функций. Понятие функций. Возможная методическая схема изучения функций в базовой школе. Методика изучения алгебраических функций.
- •Методика изучения числовых последовательностей и прогрессий.
- •Методика введения и изучения понятия производной в средней школе.
- •Использование свойств тригонометрических функций в курсе математики в средней школы.
- •Методика обучения школьников решению текстовых задач арифметическим методом и методом составления уравнений и неравенств.
- •I. Арифметический метод.
- •II. Алгебраический метод.
- •Методические особенности изучения тригонометрических функций в средней школе. Построение графиков тригонометрических функций.
- •2.26 Использование понятия производной в курсе алгебры средней школы.
2.7 Обобщение понятия степени в школьном курсе математики.
Определение: Корнем n-ой степени из чиста a называется такое число, n-я степень которого равна a.
Согласно
данному определению корень n-ой
степени из числа a
– это решение уравнения xn=a.
Число корней этого уравнения зависит
от n
и a.
Рассмотрим функцию f(x)=xn.
Как известно, на промежутке [0; +)
эта функция при любом n
возрастает и принимает все значения из
промежутка [0; +).
По теореме о корне уравнение xn=a
для любого a
[0;
+)
имеет неотрицательный корень и при том
только один. Его называют арифметическим
корнем n-ой
степени
из
числа a
и обозначают
![]() ;
число
;
число
![]() называют показателем
корня,
а само число
называют показателем
корня,
а само число
![]() - подкоренным
выражением.
Знак
- подкоренным
выражением.
Знак
![]() называют так же радикалом.
называют так же радикалом.
Определение:
Арифметическим
корнем n
-ой степени из числа a
называют неотрицательное число, n
-я степень которого равна a
. При четных n
функция f(x)=xn
четна. Отсюда следует, что если a>0
, то уравнение xn=a
,кроме корня
![]() ,
имеет также корень
,
имеет также корень
![]() .
Если
.
Если
![]() ,
то корень один:
,
то корень один:
![]() ;
если
;
если
![]() ,
то это уравнение корней не имеет,
поскольку четная степень любого числа
неотрицательна.
,
то это уравнение корней не имеет,
поскольку четная степень любого числа
неотрицательна.
При
нечетных значениях n
функция f(x)=xn
возрастает на всей числовой прямой; её
область значений – множество всех
действительных чисел. Применяя теорему
о корне, находим, что уравнение xn=a
имеет один корень при любом a
и, в частности, при a<0
. Этот корень для любого значения
a
обозначают
.
Для корней нечетной степени справедливо
равенство
![]() .
В самом деле,
.
В самом деле,
![]() ,
т.е. число –
есть корень
-й
степени
,
т.е. число –
есть корень
-й
степени
из
![]() .
Но такой корень при нечетном
единственный. Следовательно,
.
.
Но такой корень при нечетном
единственный. Следовательно,
.
Замечание
1:
Для любого действительного
![]()
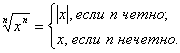
Замечание 2: Удобно считать, что корень первой степени из числа a равен a . Корень второй степени из числа a называют квадратным корнем, а корень третьей степени называют кубическим корнем.
Напомним известные свойства арифметических корней n -ой степени.
Для любого натурального n , целого k и любых неотрицательных целых чисел a и b справедливы равенства:
1.
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]()
5.
![]() .
.
Степень с рациональным показателем.
Выражение an определено для всех a и n , кроме случая a=0 при n<=0 . Напомним свойства таких степеней.
Для
любых чисел a
, b
и любых целых чисел m
и n
справедливы равенства:
![]() ;
;
![]() ;
;
![]()
Отметим
так же, что если
![]() ,
то
,
то
![]() при
при
![]() и
и
![]() при
при
![]() .
.
Определение:
Степенью числа
![]() с рациональным показателем
с рациональным показателем
![]() ,
где
,
где
![]() – целое число, а
– натуральное
– целое число, а
– натуральное
![]() ,называется
число
,называется
число
![]() .
.
Итак,
по определению
![]() .
.
При сформулированном определении степени с рациональным показателем сохраняются основные свойства степеней, верные для любых показателей (разница заключается в том, что свойства верны только для положительных оснований).
2.8 Исторические и логические последовательности изучения числовых множеств. Общий принцип расширения числовых множеств. Общая схема изучения новых чисел.
Первое
расширение понятия о числе, кот. учащиеся
усваивают после ознакомления с нат-ми
числами, - это добавление нуля. Сначала
0 – знак для обозначения отсутствия
числа. Почему же нельзя делить на нуль?
Разделить – значит найти
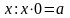 .
2 случая: 1)
.
2 случая: 1)
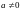 ,
следовательно, надо найти
,
следовательно, надо найти
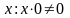 .
Это невозможно. 2)
.
Это невозможно. 2)
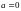 ,
следовательно, надо найти
,
следовательно, надо найти
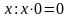 .
Таких
.
Таких
 сколько угодно, что противоречит
требованию однозначности каждой
арифметической операции.
сколько угодно, что противоречит
требованию однозначности каждой
арифметической операции.
Изучение нового числового множества идет по единой схеме:
необходимость новых чисел;
введение новых чисел;
сравнение (геометрическая интерпретация);
действия над числами;
законы.
В курсе математики 5–6 классов имеет место построение мн-ва рац чисел. Следует отметить, что последовательность расширений не однозначна. Возможны варианты:
N,
0
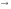 Обыкновенные
дроби
Десятичные
дроби
Рац числа (введение отриц чисел)
Обыкновенные
дроби
Десятичные
дроби
Рац числа (введение отриц чисел)
N, 0 Десятичные дроби Обыкновенные дроби Рац числа (введение отриц чисел)
N, 0 Десятич дроби Отриц числа Обыкнов дроби Рац числа (целые и дробные, положит и отриц)
N, 0 Целые числа Десятич дроби (положит) Обыкнов дроби (положит) Рац числа (введение отриц чисел)
N, 0 Дробные (обыкновенные и десятичные) Рациональные (введение отриц чисел)
Методика введения понятия «иррациональное число»
Существует три подхода к введению понятия «иррациональное число».
I. При первом подходе можно выделить 3 основных этапа введения понятия: мотивационный, введение понятия, первичное закрепление.
1
 .
Мотивационный
этап.
На этом этапе можно предложить решить
следующую задачу: «Найти сторону
квадрата, площадь которого равна 2».
Алгебраической моделью ситуации является
уравнение
.
Мотивационный
этап.
На этом этапе можно предложить решить
следующую задачу: «Найти сторону
квадрата, площадь которого равна 2».
Алгебраической моделью ситуации является
уравнение
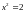 .
Решением этого ур-ния (с учетом того,
что длина выражается положит числом)
является арифметический квадратный
корень из 2. Это число. Встает вопрос:
«Какому числовому мн-ву принадлежит
это число?»
.
Решением этого ур-ния (с учетом того,
что длина выражается положит числом)
является арифметический квадратный
корень из 2. Это число. Встает вопрос:
«Какому числовому мн-ву принадлежит
это число?»
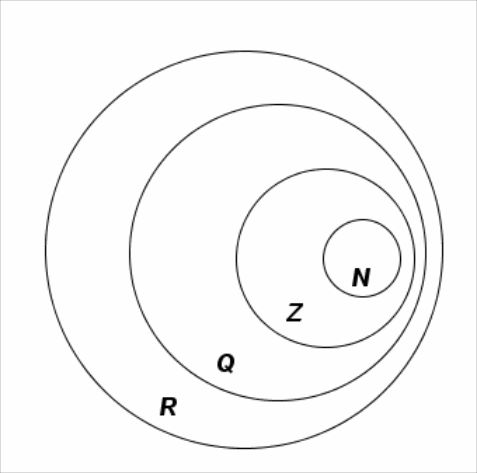
2. Этап введения понятия. Проиллюстрировать этот этап на практике.
Введение понятия «иррац число» завершается расширением мн-ва рац чисел до мн-ва действит чисел, структуру к-го можно изобразить с помощью кругов Эйлера.
3. Этап первичного закрепления. На этом этапе целесообразно решать задачи на установление взаимосвязи известных числовых мн-в, сравнение чисел, изображение чисел точками координатной прямой.
II. При 2-м подходе к ведению понятия «иррац число» можно предложить ученикам след задания.
Примеры.
1) Найдите длину отрезка
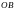 при выбранной единице измерения
при выбранной единице измерения
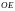 .
.
Э
![]() та
задача иллюстрирует, что процесс
измерения может быть бесконечным, а
отрезки несоизмеримыми.
та
задача иллюстрирует, что процесс
измерения может быть бесконечным, а
отрезки несоизмеримыми.
2)
Вычислите длины отрезка, если он
составляет
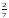 единичного отрезка. Ответ.
единичного отрезка. Ответ.
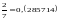 .
.
3) Приведите геометрич док-во того, что отношение площади квадрата, построенного на диагонали данного квадрата, к площади данного равно 2. Ответ. Длина диагонали квадрата равна числу, квадрат которого равен 2; при измерении длины диагонали (при условии, что единица измерения – длина стороны данного квадрата) получается бесконечная непериодическая десятичная дробь.
4) Приведите строгое док-во, что не существует рац числа, квадрат к-го равен двум.
5) Дайте определение иррационального числа.
6) Постройте множество действительных чисел.
III. При 3 подходе можно привести формулировку опред-ия и проиллюстрировать его примерами.
Методика введения понятия «комплексное число»
При первом подходе к введению понятия «комп-ое число» можно воспользоваться след. методикой.
1. Устанавливается взаимно однозначное соответствие между множеством действительных чисел и множеством точек числовой прямой. Утверждается (с привлечением теории геометрии), что существует взаимно однозначное соответствие между парами чисел и точками координатной плоскости. И как следствие: каждую пару действительных чисел, записанных в определенном порядке, логично рассматривать как некоторое новое число, изображаемое некоторой точкой координатной плоскости.
Пара
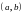 действительных чисел, заданных в
определенном порядке, наз. комплексным
числом.
действительных чисел, заданных в
определенном порядке, наз. комплексным
числом.
2.
Выделяется подмн-во
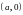 изображаемое точками оси абсцисс,
которое явл. геометрическим образом
мн-ва действительных чисел. Устанавливается
соответствие между множеством действ-ых
чисел и мн-ом комплексных чисел.
Комплексное число вида
– действительное число.
изображаемое точками оси абсцисс,
которое явл. геометрическим образом
мн-ва действительных чисел. Устанавливается
соответствие между множеством действ-ых
чисел и мн-ом комплексных чисел.
Комплексное число вида
– действительное число.
Комплексное
число вида
,
где
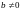 ,
называется мнимым
числом.
Комплексное число вида
,
называется мнимым
числом.
Комплексное число вида
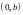 ,
где
,
называется чисто
мнимым числом.
Для числа вида
вводятся понятия: (а) – действительная
часть комплексного числа, (
,
где
,
называется чисто
мнимым числом.
Для числа вида
вводятся понятия: (а) – действительная
часть комплексного числа, (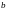 )
– мнимая часть комплексного числа.
)
– мнимая часть комплексного числа.
Далее определяются действия на множестве комплексных чисел, заданных парами. И только затем вводится мнимая единица, алгебраическая и тригонометрическая формы записи комплексного числа и правила выполнения действий с учетом формы записи.
При подходе Ш.А. Алимова к введению понятия «комплексного числа» рекомендуется следующая методика работы.
1.
Мотивационный момент: нахождение корней
уравнения
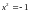 ;
введение i
как
значения квадратного корня из – 1.
;
введение i
как
значения квадратного корня из – 1.
Комплексными
числами
наз. выражения вида
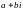 ,
где а
и
– действительные числа, а i
– некоторый символ такой, что
,
где а
и
– действительные числа, а i
– некоторый символ такой, что
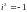 .
.
2. Здесь же опр-тся сопутствующие понятия: действительная и мнимая части комплексного числа.
3. Далее вводятся действия с комплексными числами в алгебраической форме, дается геометрическая интерпретация комплексного числа, тригонометрическая форма записи и действия с комплексными числами в тригонометрической форме записи.
Классификация множества комплексных чисел:
Комплексные числа
Действительные числа
Мнимые числа

Рациональные числа
Иррациональные числа
Целые числа
Дробные числа (положительные и отрицательные)

Натуральные числа и 0
Отрицательные целые числа
