2. Назначение, этапы проведения и ограничения применения двухфакторного дисперсионного анализа.

Принципиально этот метод не отличается от однофакторного дисперсионного анализа. Однако позволяет оценивать не только влияние каждого фактора, но и взаимодействие факторов: зависимость влияния одних факторов от уровня других. Дает возможность получить наиболее интересные результаты исследования.

Математическая модель для двухфакторного дисперсионного анализа предполагает выделение двух основных частей вариации зависимой переменной: внутригрупповой, случайные причины, межгрупповой, влияние фактора. Межгрупповая изменчивость имеет 3 уровня: влияние 1-ого фактора, влияние 2-ого фактора, взаимодействие факторов.

Соответственно дда включает в себе проверку 3 гипотез.

Взаимодействие факторов – влияние одного фактора на зависимую переменную проявляется по-разному на разных уровнях другого фактора. Для обнаружения статистически достоверного взаимодействия факторов полезны графики средних значений.

Ограничения: заметное различие выборок по численности, различие дисперсий статистически доказано, метод считается неприменимым. Число наблюдений в каждой выборке не меньше 2(желательно – не менее 5). Проверяется однородность дисперсии, если сравниваемые выборки заметно различаются по численности.

Схема дда принципиально не отличается от ода.

Выделение групповой и межгрупповой составляющих изменчивости зависимой переменной.

Отличие в выделении дополнительных составляющих. где SS_A , SS_B

– суммы квадратов для фактора А и В, а SS_AB – сумма квадратов для взаимодействия факторов.

, k – число уровней фактора А, l – число уровней фактора В, M_ij – среднее значение для члена выборки ij.

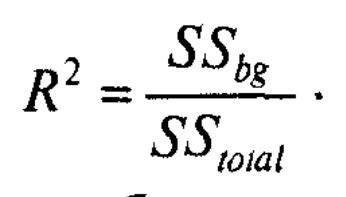коэффициент детерминации, доля общей дисперсии зависимой переменной, обусловлена совокупным влиянием факторов. Чем он больше, тем больше влияние факторов.

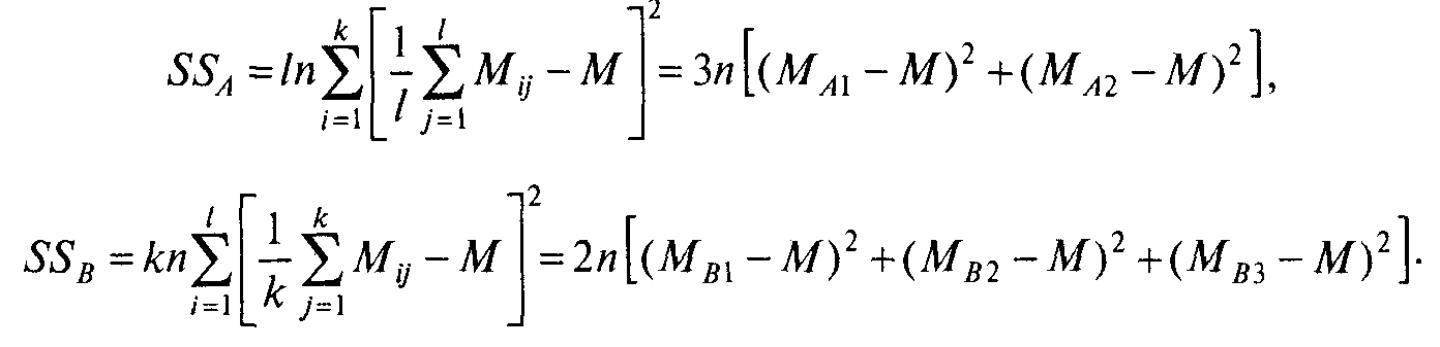
Числа степеней свободы: для общей df_tot = N-1, для фактора А df_A = k-1, для фактора В df_B = l – 1, для взаимодействия факторов df_AB = df_A xdf_B, для внутригрупповой df_wg = df_tot – df_A - df_B – df_AB = N- kxl, для общей межгрупповой df_bg= kxl – 1.

Средние квадраты.

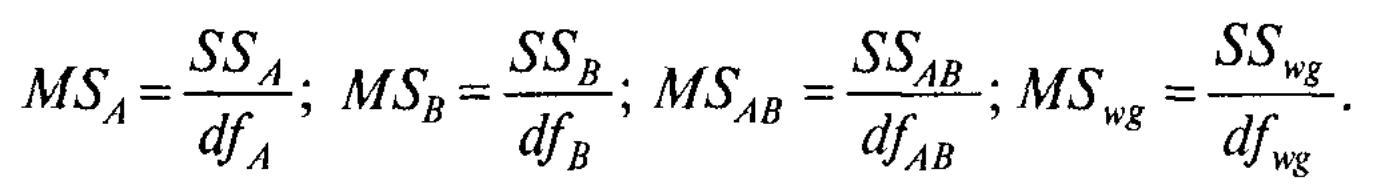
Вычисляются F-отношения,

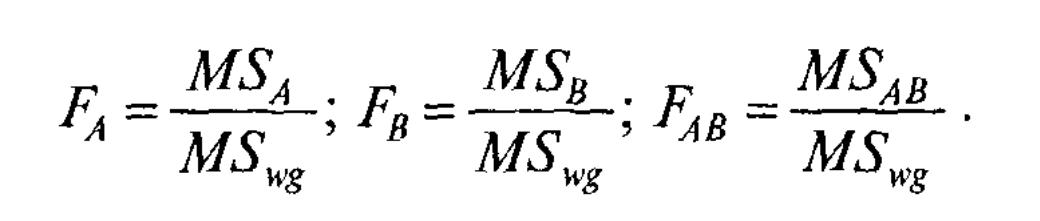
Для определения р-уровня значимости каждого из F-отношений вычисленное эмпирическое значение сравнивается с критическтм значением для степеней свободы, соответствующих числителю и знаменателю F- отношения.

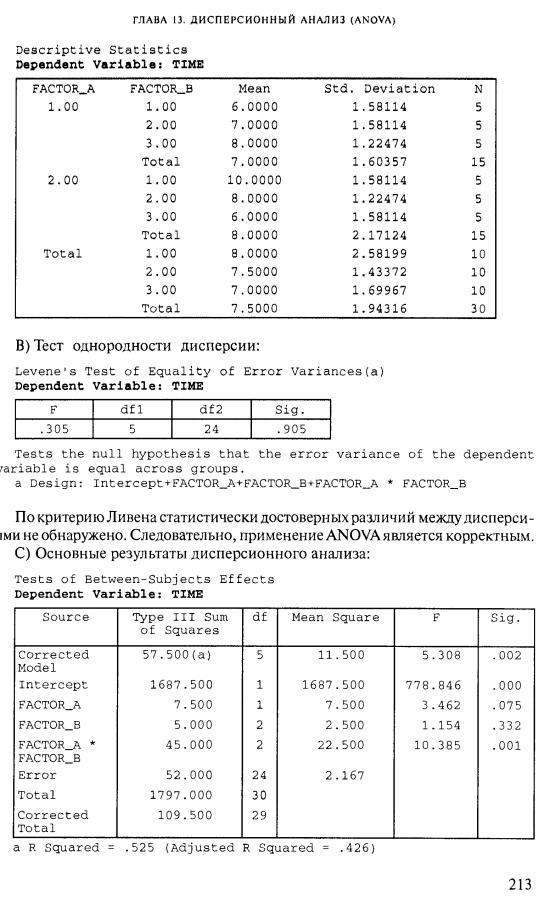
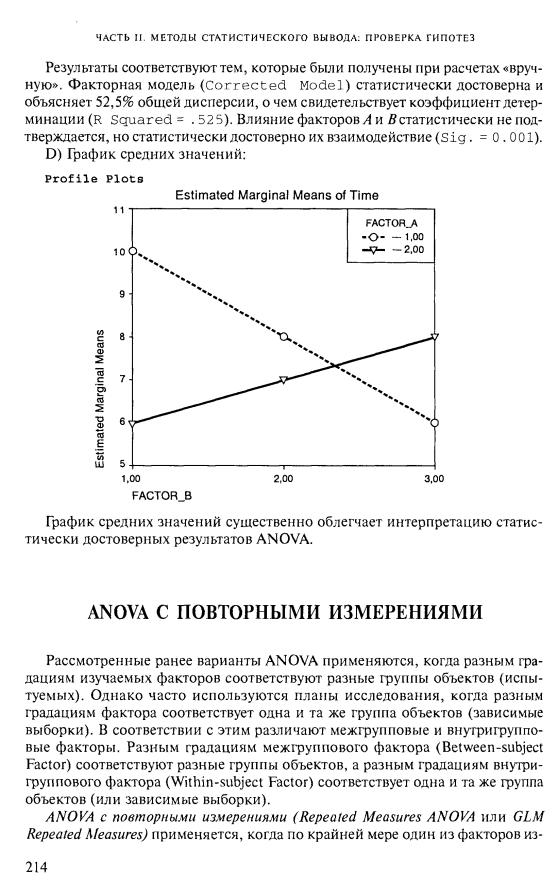
3. Дополнительные возможности двухфакторного дисперсионного анализа по сравнению с однофакторным, смысл выражения «влияние взаимодействия факторов», формула полной дисперсии данных.

Принципиально этот метод не отличается от однофакторного дисперсионного анализа. Однако позволяет оценивать не только влияние каждого фактора, но и взаимодействие факторов: зависимость влияния одних факторов от уровня других. Взаимодействие факторов – влияние одного фактора на зависимую переменную проявляется по-разному на разных уровнях другого фактора.

Полная дисперсия определяется по формуле:

Дисперсия отклонений в таком виде - несмещенная оценка и называется стандартной ошибкой регрессии. N-2 - может быть интерпретировано как число степеней свободы.

4. Понятия внутригрупповой и межгрупповой дисперсии и их значение в дисперсионном анализе

Факторная(межгрупповая) составляющая изменчивости обусловлена различием средних значений под влиянием фактора. Случайная(внутригрупповая) составляющая изменчивости обусловлена влиянием неучтенных причин. Соотношение первой и второй из указанных составляющих изменчивости и есть основной показатель, определяющий статистическую значимость влияния фактора (различия средних значений групп, соответствующих уровням фактора).

Дисперсия и квадратный корень из дисперсии, называемый стандартным отклонением, характеризуют среднее отклонение от среднего значения выборки.

5. Переменные, система статистических гипотез и принцип построения F-отношений в однофакторном дисперсионном анализе.

Независимая переменная – качественный признак, имеющий две и более градации - фактор. Каждой градации соответствует выборка объектов. Зависимая переменная – изменяющаяся под влиянием независимых переменных, представлена в метрической шкале. Однофакторный дисперсионный анализ используется при изучении влияния одного фактора на зависимую переменную. Проверяется одна гипотеза о влиянии фактора на эту переменную. Нулевая гипотеза содержит утверждения о равенстве средних значений. При ее отклонении принимается альтернативная гипотеза о том, что, по крайней мере, два средних значения различаются. Результатом является принятие или отклонение нулевой статистической гипотезы о равенстве средних значений, соответствующих разным уровням фактора. Основной показатель – р-уровень значимости критерия F-Фишера. Основным показателем считается F-отношение – эмпирическое значение F-Фишера. Чем больше величина отношения межгруппового к внутригрупповому среднему квадрату, тем больше оснований считать, что сравниваемые средние значения различаются. Процедура проверки H₀ подразумевает направленную альтернативу, так как ее отклонению соответствует только большее значение F. Поэтому для определения р-уровня значимости при вычислениях применяются таблицы критических значений F- распределения для направленных альтернатив. Для одних и тех же df уровень значимости возрастает при возрастании F.