Дисперсионный анализ

1. Назначение, этапы проведения и ограничения применения однофакторного дисперсионного анализа.

В соответствии с принятой классификацией дисперсионный анализ – это метод сравнение нескольких выборок по признаку, измеряемого в математической шкале( более двух). Решает задачу сравнения средних значений, как в критерии Стьюдента, только выборок больше двух. Допускается сравнение выборок не по одному основанию. Проявляется в двух отношениях: 1. Этот метод используется в рамках планирования эксперимента. 2. Для сравнения средних значений анализируются компоненты дисперсии изучаемого признака. Метод разработан Фишером для анализа результатов экспериментальных исследований.

Типичная схема эксперимента сводится к изучению влияния независимой переменной на зависимую переменную. Независимая переменная – качественный признак, имеющий две и более градации - фактор. Каждой градации соответствует выборка объектов. Зависимая переменная – изменяющаяся под влиянием независимых переменных, представлена в метрической шкале.

Однофакторный дисперсионный анализ используется при изучении влияния одного фактора на зависимую переменную. Проверяется одна гипотеза о влиянии фактора на эту переменную. Математическая модель однофакторного дисперсионного анализа предполагает выделения в общей изменчивости зависимой переменной двух ее составляющих. Факторная(межгрупповая) составляющая изменчивости обусловлена различием средних значений под влиянием фактора. Случайная(внутригрупповая) составляющая изменчивости обусловлена влиянием неучтенных причин. Соотношение первой и второй из указанных составляющих изменчивости и есть основной показатель, определяющий статистическую значимость влияния фактора (различия средних значений групп, соответствующих уровням фактора).

Нулевая гипотеза содержит утверждения о равенстве средних значений. При ее отклонении принимается альтернативная гипотеза о том, что, по крайней мере, два средних значения различаются.

Ограничения: если дисперсии выборок различаются статистически достоверно, то метод неприменим. Для проверки однородности дисперсии применяется критерия Ливена. Формально численность выборок не должна быть меньше 2 объектов, не меньше 5 объектов в каждой выборке фактически.

Существует альтернатива: сравнение независимых выборок по критерию Н-Краскала-Уоллеса. Результатом является принятие или отклонение нулевой статистической гипотезы о равенстве средних значений, соответствующих разным уровням фактора. Основной показатель – р-уровень значимости критерия F-Фишера. Возможны множественные сравнения средних значений, позволяющие сделать вывод, как различаются друг от друга средние значения для разных градаций фактора.

Общая сумма квадратов – показатель общей изменчивости зависимой переменной и представляет собой числитель дисперсии. Равна сумме межгрупповой и внутригрупповой сумм квадратов.

Межгрупповая сумма квадратов – показатель изменчивости между k группами, каждая численностью n объектов.

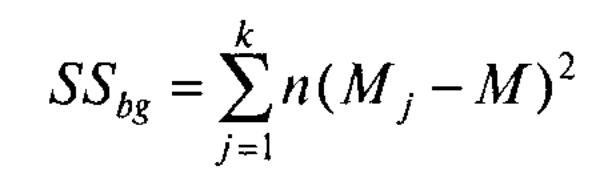
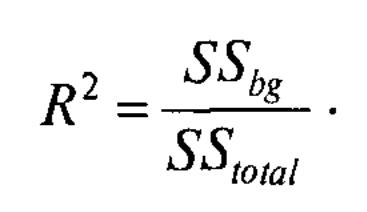показывает долю общей дисперсии зависимой переменной, обусловленную влиянием фактора. Идентично по смыслу квадрату коэффициента корреляции в регрессионном анализе, называется коэффициентом детерминации(R²), принимает значения от 0 до 1, чем больше показатель, тем больше влияние изучаемого фактора на дисперсию зависимой переменной. Помноженный на 100 – выражает процент учтенной дисперсии.

Внутригрупповая сумма квадратов – показатель случайной изменчивости.

Для сопоставления сумм квадратов используются средние квадраты (MS). Средние квадраты – частное от деление суммы квадратов на соответствующее число степеней свободы(df). Общее число степеней свободы соответствует общей сумме квадратов и равно: N-1. Число степеней свободы для межгрупповой суммы квадратов равно ислу слагаемых минус один(число групп минус 1). Число степеней свободы для внутригрупповой суммы квадратов:

Общий средний квадрат – общая дисперсия.

Основным показателем считается F-отношение – эмпирическое значение F-Фишера. Чем больше величина отношения межгруппового к внутригрупповому среднему квадрату, тем больше оснований считать, что сравниваемые средние значения различаются.

Процедура проверки H₀ подразумевает направленную альтернативу, так как ее отклонению соответствует только большее значение F. Поэтому для определения р-уровня значимости при вычислениях применяются таблицы критических значений F- распределения для направленных альтернатив. Для одних и тех же df уровень значимости возрастает при возрастании F.