Лекция 19. Особые случаи ламинарного течения Ламинарное течение в зазорах Ламинарное течение в плоских зазорах

Рассмотренные выше зависимости, как уже отмечалось, действительны для труб круглого сечения, но они нуждаются в уточнении, если форма сечения потока отличается от окружности. Такие потоки имеют место в каналах и проходных щелях гидроаппаратуры, в гидромашинах и во многих других устройствах.

В начале рассмотрим ламинарное течение в плоском зазоре с неподвижными стенками, расстояние между которыми равно a.

Начало системы координат для простоты поместим в середину зазора. В этом зазоре рассмотрим два поперечных сечения потока 1 и 2, находящихся на расстоянии l друг от друга. Ширину рассматриваемой части потока обозначим . На участке l выделим объём жидкости в форме прямоугольного параллелепипеда, имеющего размеры , и симметрично расположенного в зазоре. Условием равномерного движения параллелепипеда будет являться равенство сил давления и сил вязкого трения, действующих в направлении движения

Знак « - » перед силой вязкого трения означает, что она направлена против движения. Знак « - » перед градиентом скорости означает, что производная отрицательна, т.е. c ростом y, в принятой системе отсчёта, скорость слоя жидкости уменьшается. По аналогии с зависимостями для трубы круглого сечения примем , поэтому приращение скорости можно представить в виде:

После интегрирования по y получим

Постоянную интегрирования C определим из условий движения жидкости у поверхности стенки, где , а . Тогда

После подстановки C в выражение для скорости элементарного слоя жидкости u примет вид

Последняя формула определяет то, как связана скорость жидкости с расстоянием от середины потока, т.е. от положения слоя жидкости в зазоре. Зная это, нетрудно определить расход жидкости в зазоре. Для этого определим сначала элементарный расход dQ через площадку высотой (толщиной) dy и шириной b, который будет равен

После интегрирования по y в пределах половины высоты щели от до , получим половину расхода через щель:

Тогда полный расход через щель будет в два раза больше:

Если учесть, что средняя скорость в щели будет , то потери напора в щели с плоскими стенками составят:

Ламинарное течение в плоских зазорах с подвижной стенкой

В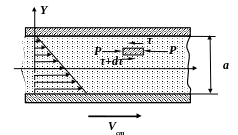 процессе работы гидроаппаратов и гидромашин может встречаться ситуация, когда одна из плоских поверхностей, образующих зазор, перемещается параллельно другой попутно или встречно направлению потока жидкости. Движущаяся поверхность за счёт сил вязкого трения увлекает за собой жидкость. Если при этом давление в жидкости постоянно, то возникает так называемое фрикционное безнапорное движение. Эпюра распределения скоростей в этом случае примет треугольный вид, причём надо заметить, что скорости относительного движения в прилегающих к стенкам слоях жидкости равны нулю. Внутри потока жидкости выделим некоторый объём прямоугольного сечения и рассмотрим действующие на него силы. В принятых условиях на торцовые поверхности действует одинаковое давление, следовательно, одинаковыми будут и силы. Тогда для достижения равновесия рассматриваемого объёма необходимо равенство касательных напряжение на его нижней и верхней поверхностях. Отсюда следует, что dτ = 0 и τ - величина постоянная. Следовательно, по закону жидкостного трения Ньютона . В этом выражении C постоянная, а знак « - » означает, что при увеличении dy приращение скорости du становится отрицательным (скорость уменьшается). В таком случае выражение для скорости примет вид

После интегрирования, получим

Постоянные интегрирования C и C₁ найдём из условий на границах потока, где при , а при (V_ст – скорость движения стенки).

Подставив эти значения в выражение для скорости, получим систему из двух уравнений

Выразив из первого уравнения , после подстановки его во второе запишем:

Отсюда постоянная C примет вид . Подставив это в выражение для C₁, будем иметь значение постоянной интегрирования .

После выяснения значений для постоянных С и С₁ получим формулу скорости u:

Средняя скорость такого фрикционного потока жидкости составляет половину скорости подвижной поверхности, что нетрудно видеть на эпюре распределения скоростей по сечению зазора:

а величину расхода можно вычислить по формуле:

Вывод из сказанного состоит в том, что в зазоре между подвижной и неподвижной поверхностями даже при отсутствии разности давления всегда будет поток жидкости, скорость которого определяется относительными скоростями поверхностей.

Если фрикционное движение происходит при перепаде давлений, то скорости движения слоёв в таком потоке складываются из скоростей, обусловленных фрикционным движением, и скоростей, обусловленных напором. Величина скорости напорного движения жидкости в плоской щели была получена ранее и выглядит следующим образом:

Скорость подвижной поверхности щели V_ст может быть направлена попутно или встречно фрикционному потоку. В этом случае скорости слоёв жидкости определяются сложением или вычитанием скоростей, обусловленных фрикционным движением, и скоростей, обусловленных напором.

При попутном движении

при встречном

Расход жидкости через плоскую щель при напорно-фрикционном движении складывается из суммы расходов при двух движениях в отдельности и составляет:

Первое слагаемое в формуле называется напорным расходом, а второе - фрикционным, который добавляется или вычитается при попутном или встречном направлении движения подвижной стенки щели.