Критерий подобия Фруда

В тех случаях, когда движение жидкости является безнапорным и происходит под действием разности нивелирных высот, условие подобия потоков описывается иначе, с помощью другого критерия подобия - числа Фруда. Этот критерий учитывает пропорциональность в отношениях сил инерции к силам тяжести. Однако для подавляющего большинства интересующих нас задач в области машиностроения этот критерий не имеет значения и рассматриваться не будет.

Заключение о подобии напорных потоков

Итак, в подобных напорных потоках имеем равенство безразмерных коэффициентов и чисел α, ζ, λ, Eu, Re, Ne. Изменение Re означает, что меняется соотношение основных сил в потоке, в связи с чем указанные коэффициенты могут также несколько меняться. Поэтому все эти коэффициенты следует рассматривать как функции Re (хотя в некоторых интервалах Re они могут оставаться постоянными).

Лекция 16. Истечение жидкости из отверстий и насадков

Истечение жидкости из отверстий и насадков (коротких трубок различной формы и сечений) характерно тем, что в этом процессе потенциальная энергия жидкости на очень коротком расстоянии и за очень короткое время превращается в кинетическую энергию струи (или капель в общем случае). При этом происходят какие-то, большие или не очень, потери напора. Подобные режимы течения жидкости возникают при вытекании жидкости из резервуаров, баков, котлов в атмосферу или пространство, заполненное жидкостью. Аналогичные явления происходят при протекании жидкости через малые отверстия и щели в направляющей, контрольной и регулирующей аппаратуре различных гидравлических систем.

Основной вопрос, на который нужно найти ответ, состоит в том, как определить расход и скорость истечения через отверстия или насадки различной формы.

Сжатие струи

П ри вытекании жидкости из резервуара через отверстие в тонкой стенке, диаметр которого значительно меньше размеров резервуара, а края отверстия имеют прямоугольную форму, диаметр вытекающей струи будет меньше размеров диаметра отверстия. Это происходит потому, что жидкость, вытекающая из резервуара, попадает в отверстие со всех направлений, а после прохождения отверстия направление движения всех частиц жидкости становится одинаковым. Изменение направления движения частиц жидкости в силу их инерционности мгновенно произойти не может. Поэтому сжатие струи обусловлено необходимостью постепенного изменения направления движения жидкости при прохождении отверстия. Так как размеры резервуара много больше размеров отверстия, боковые поверхности и свободная поверхность не могут оказывать влияния на направление входа жидкости в отверстие, то в этом случае наблюдается совершенное сжатие струи. Такое сжатие является наибольшим, и оно достигается на расстоянии примерно равном диаметру отверстия. Степень сжатия выражается коэффициентом сжатия :

,

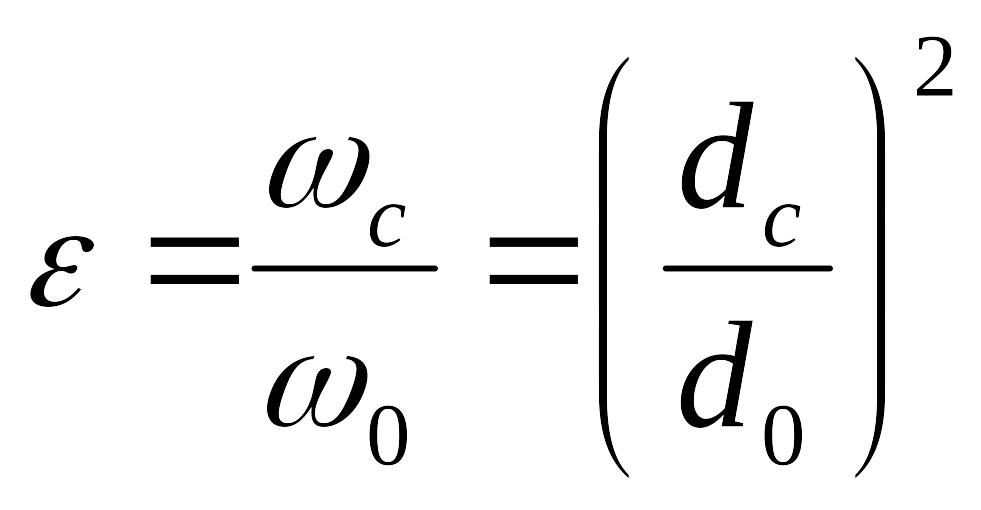где - площадь и диаметр отверстия,

- площадь и диаметр совершенно сжатой струи.

В том случае, если истечение происходит из резервуара такой формы, что его стенки влияют на траекторию движения частиц при входе в отверстие, наблюдается несовершенное сжатие струи.

В следствие того, что боковые стенки резервуара перед отверстием формируют направление движения жидкости, струя после отверстия сжимается в меньшей степени, чем при вытекании из практически бесконечного резервуара. По этой причине меняется коэффициент сжатия струи. Формулы для определения этого сжатия для разных жидкостей и разных условий истечения - эмпирические. Например, для круглого центрального отверстия в тонкой торцовой стенке трубы и для маловязких жидкостей коэффициент сжатия можно находить по следующей эмпирической формуле в долях от коэффициента сжатия при совершенном сжатии струи

;

где ;

где, в свою очередь, - площадь отверстия,

- площадь сечения резервуара (в приведённом примере площадь поперечного сечения трубы).