Лекция 13. Турбулентное течение жидкости

Напомним, что турбулентное движение жидкости отличается интенсивным вихреобразованием, приводящим к перемешиванию слоёв. В потоке наблюдаются постоянные пульсации давлений и скоростей, как по величине, так и по направлению. Турбулентное течение имеет неустановившийся характер, а траектории движения частиц жидкости постоянно и хаотически меняются. На практике такое движение встречается достаточно часто при высоких скоростях потока и малой вязкости жидкости. Вследствие того, что при турбулентном течении потока нет слоистости, закон трения Ньютона неприменим. По причине сложности турбулентного движения и его аналитического исследования, пока нет достаточно строгой теории этого течения. Существует полуэмпирическая приближённая теория Прандтля, элементы которой будут затронуты ниже, при рассмотрении вопроса о вязком трении в турбулентных потоках.

Потери энергии (потери напора на трение) при турбулентном течении жидкости больше, чем при ламинарном, из-за значительных потерь на вихреобразование, перемешивание и изменение траекторий.

В гидравлике для практических расчётов турбулентного течения жидкости в трубах используют экспериментальные систематизированные данные, применяемые на основе теории подобия. Основной расчётной формула для определения потерь напора в круглых трубах является уже известная формула Дарси

,

однако коэффициент , в данном случае это коэффициент на трение по длине при турбулентном течении, и он существенно отличается от , используемом при ламинарном движении жидкости.

Вязкое трение при турбулентном движении

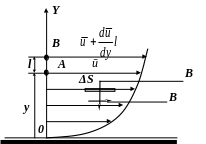
Выделим в турбулентном потоке, движущимся параллельно твёрдой стенке, элементарную площадку ΔS и определим касательное напряжение τ, возникающее за счёт пульсаций скоростей . Через площадку в перпендикулярном потоку направлении, проходит расход жидкости

.

Масса жидкости, проходящая через площадку за время Δt, равна

За счёт составляющей пульсаций скорости эта масса получит приращение количества движения

.

Приращение количества движения равно импульсу силы, т.е.

;

где сила и тогда касательное напряжение будет равно

,

а его осреднённое по времени значение можно представить в виде

.

Определённое таким образом касательное напряжение вычислить очень трудно из-за неизвестных значений и , поэтому, чаще всего рассматривается приближённое решение.

Представим, что малый объём жидкости, находящийся в точке A и имеющий скорость , в результате турбулентного перемешивания переместился в точку B, расположенную на расстоянии l от точки A приобрёл скорость .

Будем считать, что пульсации скоростей и пропорциональны приращению скорости рассматриваемого объёма жидкости, т.е.

, .

Тогда можно представить в виде

,

где коэффициент пропорциональности включён в величину l, знак совпадает со знаком производной . Величина l носит называние путь перемешивания.

Последнее уравнение обычно преобразовывают к виду

,

где С_Т – коэффициент перемешивания, или коэффициент турбулентного обмена который равен

.

Полученное уравнение аналогично уравнению касательного напряжения при ламинарном режиме. Коэффициент C_Т значительно превышает по величине динамическую вязкость и зависит от числа Рейнольдса.