4.11. Упрощения системы уравнений теории омд

В связи с математическими трудностями решения полной системы дифференциальных уравнений теории ОМД применяют упрощающие допущения. Эти допущения не должны находиться в большом противоречии с физикой конкретного процесса деформации. В то же время они должны облегчить вычисления. К числу таких допущений относится:

1) предположение об идеальной пластичности;

2) об изотермичности течения металла;

3) о его несжимаемости;

4) о достаточно медленном течении металла без массовых сил;

5) о плоском деформированном и напряженном состоянии.

1. Идеально – пластичным называется материал, который не проявляет упрочнения, то есть по мере изменения H или накопления .

T=const.

По условию текучести Мизеса то есть металл переходит в пластическое состояние при некотором напряженном состоянии, интенсивность касательных напряжений которого .

.

Это идеализация, так как у реальных металлов:

.

Рис. Зависимость интенсивности касательных напряжений Т от интенсивности скорости деформации Н для реальных металлов

Но гипотеза об идеальной пластичности существенно упрощает решение задач. Физические уравнения связи:

2.Течение называется изотермическим, если за все время деформации в любой точке деформируемого тела , то есть разогрев от работы деформации и теплообмен с окружающей средой в расчет не принимают. Это допущение в ряде случаев является оправданным. Однако в каждом конкретном случае необходимо проверять его справедливость. При изотермическом процессе считают известной и нет надобности решать дифференциальные уравнения теплопроводности.

3. Гипотеза несжимаемости с достаточно высокой степенью точности выполняется для многих металлов.

4. Процессы ОМД достаточно медленны, то есть плотность сил инерции не влияет на напряженно – деформированное состояние металла. Мала также, как правило, и плотность других массовых сил (например сил тяжести). Поэтому дифференциальное уравнение движения сплошной среды

упрощается и переходит в дифференциальное уравнение равновесия

.

При изучении штамповки взрывом, магнитоимпульсной штамповки следует все же пользоваться дифференциальным уравнением движения.

Допущения о плоском деформированном состоянии и плоском напряженном состоянии рассмотрим отдельно.

4.12. Плоское деформированное состояние

Деформированное состояние называется плоским, если векторы скорости течения всех частиц металла лежат в параллельных плоскостях, например координатной плоскости xoy. Тогда:

(1)

Подобное состояние возникает в длинных призматических телах, ориентированных длинной стороной вдоль оси z. Нагрузки действуют в плоскостях, параллельных xoy и во всех этих плоскостях они одинаковы.

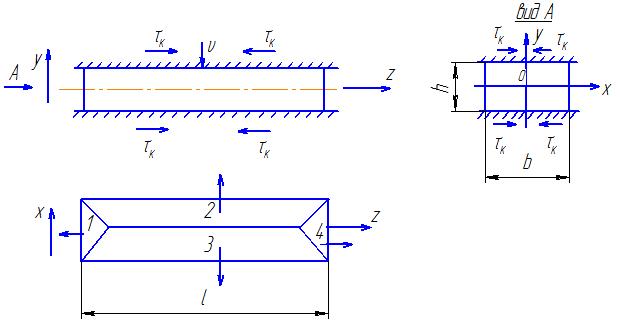
Рис. Схема плоского деформированного состояния

Если считать трение изотропным, то есть независящим от направления, то тогда в соответствии с законом наименьшего сопротивления все частицы металла будут скользить в направлении наикратчайшего расстояния до края заготовки. Поэтому заготовку можно разделить линиями, равноудаленными от границ, на зоны 1… 4.

С учетом этого разбиения на зоны можно принять, что течение металла в направлении z пренебрежительно мало, по сравнению с течением в направлении оси x. Таким образом говорят что весь смещенный в направлении y металл течет в направлении x, то есть .

Можно также считать, что скорости и одинаковы во всех поперечных сечениях, если мы будем перемещаться вдоль оси z. То есть эти скорости независимы от z. Таким образом и мы получим выражение (1).

– плоское деформированное состояние.

Интенсивность скорости деформации H для несжимаемого материала при плоской деформации:

Для изотропного несжимаемого материала:

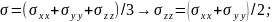
Подставляя напряжение в формулу для T получим:

Условие текучести для идеальной пластичности

Тогда:

зависит от x и y.