10. Трение в омд
Трение в ОМД отличается от трения в деталях машин:
1. В деталях машин нормальные напряжения в механических парах в несколько раз меньше, чем предел текучести металла, из которого они изготовлены. В ОМД нормальные напряжения на контактной поверхности выше, чем предел текучести металла.
2.
Часто в процессах ОМД металл нагревают
до высоких температур (выше
).
Поверхность металла покрывается слоем
окалины, который изменяет условия
трения.
3. В деталях машин трущиеся поверхности одни и те же, так как их свойства в процессе работы изменяются очень медленно. В процессах ОМД происходит постоянно обновление поверхности за выхода внутренних частиц металла на контактную поверхность при пластической деформации.
Теоретическое описание механизма трения сводится к тому, что требуется определить силы взаимодействия 2–х шероховатых поверхностей, имеющих различные механические свойства. По высоте зоны, разделяющей эти поверхности, свойства изменяются.
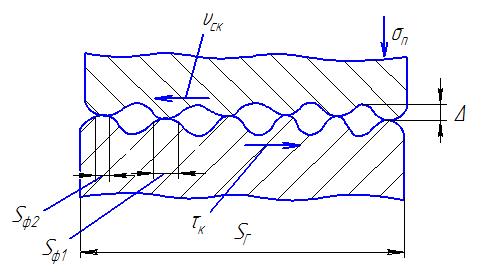
Рис. Схема контактирования заготовки и инструмента:
-
высота микронеровностей;
- геометрическая площадь контакта;
-
фактическая площадь контакта;
- нормальное контактное напряжение
;
.
(1)
Здесь N – количество площадок фактического контакта.
Таким образом, напряжения контактного трения:
.
(2)
Указанные функции (1) и (2) найти в явном виде на основании теоретических выкладок не удается. Поэтому применяют методы экспериментальной оценки сил трения.
В деталях машин широко применяют закон трения Кулона:
(3)
где
– коэффициент трения. Этот закон
применяется и в ОМД. Здесь
зависит от многих факторов. По условию
пластичности касательные напряжения
всегда меньше или равны
.
Поэтому в (3)
с ростом
увеличивается до
:
.
При дальнейшем увеличении
остается постоянным.
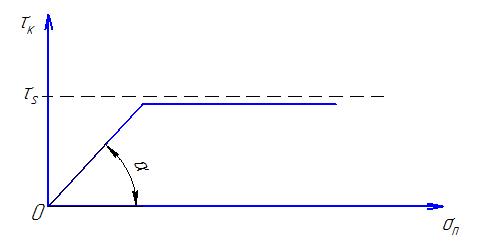
Рис. График зависимости от
Исходя из этого, Зибелем был выдвинут следующий закон трения:
(4)
Так
как
может быть
Смысл
коэффициента
можно определить сопоставляя формулы
(1) и (4). В законе Зибеля
характеризует соотношение площадей
фактического и геометрического контакта.
Когда
(предельное значение) мы допускаем, что
по всей контактной поверхности происходит
сдвиг металла (тонкий слой металла
заготовки «прилипает» к поверхности
инструмента и происходит его сдвиг
относительно основной части заготовки).
При
Так как функцию (1) теоретически не
определить,
находят экспериментально.
Закон Кулона следует применять при холодной ОМД, когда величина достигает весьма больших значений, а на порядок меньше за счет малого .
Например:
при холодной листовой прокатке со
смазкой
при листовой штамповке
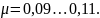
Закон Зибеля следует применять при горячей ОМД, так как в этом случае напряжения трения близки к пределу текучести на сдвиг.
При
горячей листовой прокатке
при горячей объемной штамповке
,
то есть по всей поверхности сдвиг.
В большинстве случаев трение играет отрицательную роль, так как чем больше трение, тем больше износ инструмента; больше усилие деформации; больше нагрузки на оборудование. Положительную роль трение играет редко, например, при прокатке на стадии захвата заготовки вращающимися бойками. Если трение мало – буксование заготовки относительно валков.
Трение
снижают путем применения смазок. Трение
может быть: сухое, полусухое (или
полужидкостное) и жидкостное. Сухое:
;
полусухое:
;
жидкостное:
.
Рис. Схема жидкостного трения
При жидкостном трении напряжения трения можно определить согласно модели Ньютона (идеально вязкая среда):
;
где
- коэффициент вязкости смазки;
- скачок скорости.
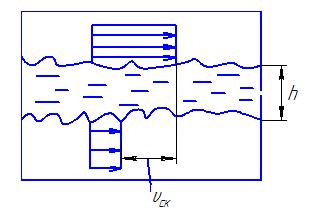
Рис. Скорости при жидкостном трении (вверху – инструмент, внизу
заготовка, h – толщина слоя смазки)
Актуальная задача – созданий условий для реализации жидкостного трения в процессах ОМД. Пример: гидромеханическая вытяжка, волочение в режиме гидродинамического трения.
При гидромеханической вытяжке жидкость сжимается в полости матрицы перемещающимися вниз пуансоном и заготовкой. Это приводит к прорыву жидкости и между матрицей и заготовкой образуется слой смазки, который обеспечивает жидкостное трение.
Рис. Схема гидромеханической вытяжки
Обычно в процессах ОМД реализуется полусухое трение. Актуальная задача – создание смазок, которые не теряли своих свойств при повышении температуры; не выдавливались с границы металл – инструмент при больших давлениях.