
- •Тема 4. Физические уравнения связи напряженного и деформированного состояния
- •4.1. Общая постановка задачи теории омд
- •4.2. Формулировка физических уравнений для изотропных металлов
- •4.3. Гипотеза единой кривой
- •4.4. Модели сплошных сред
- •1. Модели идеальной упругой среды (модель Гука).
- •2. Линейно – вязкая среда (среда Ньютона).
- •3. Жестко – пластическая среда (среда Сен – Венана):
- •4.5. Линейная теория упругости
- •4.6. Теория пластического течения
- •4.7. Условие пластичности
- •4.8. Полная система дифференциальных уравнений теории омд
- •4.9. Граничные условия и виды границ
- •10. Трение в омд
- •4.11. Упрощения системы уравнений теории омд
- •4.12. Плоское деформированное состояние
- •4.13. Плоское напряженное состояние
4.8. Полная система дифференциальных уравнений теории омд
Для полного определения напряженного и деформированного состояния металла в каждой точке деформированного тела в каждый момент времени нам нужно определить:
 -
6 штук;
-
6 штук;
 - 6 штук;
- 6 штук;
 - 3 штуки.
- 3 штуки.
Необходимо
также знать температуру
 .
Всего 16 неизвестных. Для их определения
мы имеем дифференцильные уравнения.
.
Всего 16 неизвестных. Для их определения
мы имеем дифференцильные уравнения.
Дифференциальные уравнения движения:

 ,
(i=x,
y,
z;
j=x,
y,
z).
(1)
,
(i=x,
y,
z;
j=x,
y,
z).
(1)
Как правило, массовыми силами и ускорениями в реальных процессах ОМД можно пренебречь. Из (1) получаем дифференциальные уравнения равновесия:
 – 3
уравнения.
(1а)
– 3
уравнения.
(1а)
Кинематические уравнения:
 -
6 уравнений. (2)
-
6 уравнений. (2)
Физические уравнения связи напряженного и деформированного состояния:
 -
6 уравнений; (3)
-
6 уравнений; (3)

Дифференциальное уравнение теплопроводности:
 -
1 уравнение (4)
-
1 уравнение (4)
Условие несжимаемости;
 -
1 уравнение. (5)
-
1 уравнение. (5)
Всего 17 уравнений.
Система (1) – (5) является полной системой дифференциальных уравнений теории пластичности.
Для решения конкретной задачи необходимо, чтобы были заданы начальные и граничные условия.
Начальные условия - известны какие – то величины (скорости, напряжения) в начале деформации при = 0.
Граничные условия – это условия на поверхностях, ограничивающих деформируемое тело.
В том случае, когда рассматривается стационарный процесс достаточно задать лишь граничные условия.
Стационарный
– это процесс, при котором механические
переменные
 в каждой точке деформируемого тела
остаются постоянными, то есть от времени
не зависит. Стационарные процессы –
прокатка, волочение; нестационарные –
штамповка.
в каждой точке деформируемого тела
остаются постоянными, то есть от времени
не зависит. Стационарные процессы –
прокатка, волочение; нестационарные –
штамповка.
4.9. Граничные условия и виды границ
Конкретность при решении задачи расчета напряжений и деформаций мы вносим путем задания граничных условий. В понятие «граничные условия» входит: форма границ тела и величины напряжений и скоростей на этих границах.
Граничные условия (ГУ) бывают следующих видов:
1.
Статические
ГУ
– когда на границе задан вектор напряжений
 .
.
 по формулам Коши можно связать с
компонентами
по формулам Коши можно связать с
компонентами
 .
.

Рис. Статические ГУ (заданы напряжения на части поверхности тела)
2. Кинематические ГУ.
На
границе задан вектор скорости перемещения
 .
.

Рис. Кинематические ГУ (заданы скорости перемещения на части
поверхности тела)
Значение
 и
и
 в каждой точке границе свои, то есть
они являются функциями координат x, y,
z.
в каждой точке границе свои, то есть
они являются функциями координат x, y,
z.
Иногда выбирают локальную систему координат: первая координата n – нормаль к поверхности, а две другие координаты лежат в касательной к поверхности плоскости. Тогда


В скобках записаны проекции векторов на оси координат.
3.
Смешанные
ГУ
– на границе заданы часть проекций
вектора напряжений и часть проекций
вектора скорости:
 или
или

Виды границ. Рассмотрим виды границ и граничные условия на них. Для примера рассмотрим схему операции свободной ковки – протяжку, осуществляющую на прессе или молоте.

Рис. Схема протяжки заготовки:
1 – контактная граница (граница металла с инструментом); 2 – свободная граница; 3 – граница жесткой области (в ЖЗ деформация упругая); ОД – очаг деформации
В общем случае форма границ 3 и 2 неизвестны и они определяются из решения задачи.
На свободной границе 2 имеем статические ГУ, так как на ней известна часть напряжений: нормальное к границе напряжение
 =
0.
=
0.
На
контактной границе 1 нормальная
составляющая скорости перемещения
металла
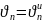 («и» - инструмент). Если это условие не
выполняется, то это означает, что металл
или внедряется в инструмент или отходит
от него.
(«и» - инструмент). Если это условие не
выполняется, то это означает, что металл
или внедряется в инструмент или отходит
от него.
Для касательных составляющих скорости возможны случаи:
а) прилипание металла – в этом случае частицы металла заготовки на границе не перемещаются в касательной плоскости относительно инструмента, т.е.
 ;
;
 .
.
Это
запись в общем случае для всех процессов
ОМД. Обычно при штамповке и ковке
= 0;
= 0. Тогда прилипание означает
 =0,
=
0. Это скорости в горизонтальной плоскости
бойка.
=0,
=
0. Это скорости в горизонтальной плоскости
бойка.
б) скольжение металла – на контактной границе имеем:
 ;
;
 .
.
Это означает, что в горизонтальной плоскости бойка частицы металла скользят по инструменту: ≠ 0, ≠ 0.
В
общем случае скорость скольжения:
 .
.
 ,
где
,
где
 ;
;
 .
.
На
контактной границе необходимо задавать
смешанные граничные условия: ( .
Напряжения
.
Напряжения
 и
и
 подчиняются закономерностям трения
скольжения.
подчиняются закономерностям трения
скольжения.
На
границе жесткой зоны 3
происходит сдвиг металла. Поэтому
касательные напряжения
 будут направлены навстречу скорости
сдвига и по величине равны
:
будут направлены навстречу скорости
сдвига и по величине равны
:
 .
Нормальные к границе скорости в ЖЗ и ОД
равны по величине. Касательная к границе
составляющая скорости равна разности
касательных скоростей в ЖЗ и ОД. Таким
образом, на границе 3 задают смешанные
ГУ.
.
Нормальные к границе скорости в ЖЗ и ОД
равны по величине. Касательная к границе
составляющая скорости равна разности
касательных скоростей в ЖЗ и ОД. Таким
образом, на границе 3 задают смешанные
ГУ.
