4.6. Теория пластического течения

Применяется при значительной величине деформаций. В реальных процессах штамповки деформация заготовки значительна. Поэтому теория пластического течения применяют для расчета напряжений и деформаций в деформируемой заготовке.

1. В этой теории принимается гипотеза о несжимаемости и изотропности. Скорость относительного изменения объема , равна:

.

Приведенное выше выражение представляет собой математическую запись условия несжимаемости.

2. Физические уравнения устанавливают связь между напряжениями и скоростями деформаций. В основе физических уравнений лежит гипотеза о коаксиальности тензоров и : направление главных нормальных напряжений и главных скоростей удлинений для изотропной сплошной среды совпадают.

Используется также гипотеза о пропорциональности девиаторов и :

.

Пропорциональность девиаторов можно записать через их компоненты:

Запишем пропорциональность девиаторов через компоненты тензоров напряжений и скоростей деформаций:

; ( ). (1)

Выражение (1) – физические уравнения связи в общем виде. Запишем эти уравнения с учетом условия несжимаемости:

. (2)

Из (2) можно записать:

.

При определении коэффициента пропорциональности учтем, что напряженное состояние характеризует интенсивность касательных напряжений Т, а деформированное состояние – интенсивность скоростей деформации сдвига H:

; .

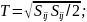
Здесь . (2)

Функция (2) устанавливается экспериментально на основе гипотезы единой кривой. То есть устанавливается в простых опытах (одноосное растяжение или сжатие, кручение), а результаты можно использовать и при других схемах напряженного состояния.

3. Используют кинематические уравнения:

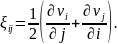
4. Используются дифференциальные уравнения равновесия:

, ( ).

4.7. Условие пластичности

Необходимо найти обобщенный критерий перехода металла в пластическое состояние при произвольной схеме нагружения.

В этот критерий должны входить не сами компоненты тензора, а его инварианты. Они являются скалярными характеристиками и не зависят от выбора системы координат.

Условие пластичности сформулированы на основе обобщения экспериментальных данных.

Рассмотрим условие текучести Мизеса. Пластическая деформация начинается тогда, когда интенсивность касательных напряжений достигает предела текучести на сдвиг:

.

Если произвести одноосное растяжение и определить напряжение начала пластического течения , получим

При одноосном растяжении , .

Если осуществить эксперимент на чистый сдвиг ( , ) и зафиксировать касательное напряжение начала пластического течения получим

Таким образом:

Экспериментально условие пластичности Мизеса проверить можно также следующим образом: берется трубчатый образец, закрытый с двух сторон. Внутрь образца подается жидкость под давлением р. Образец растягивается с силой Р и к его концам прикладывается крутящий момент М.

Рис. Деформация трубчатого образца

; .

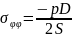Так как S мало изменение по толщине незначительно.

;

пренебрегаем и считаем его равным нулю.

(так как .

Получили плоское напряженное состояние:

По компонента этого тензора можно рассчитать интенсивность касательных напряжений Т и сравнить его с пределом текучести металла на сдвиг . Величину можно определить экспериментально в опыте на чистый сдвиг.

Для проверки условия текучести Мизеса смотрим: течет металл при .