Лекция 9
Продолжение лекции 8
-
«…И только теперь, когда ты вышел из берегов, увидел океан и познал свое ничтожество, с тобой можно говорить о великой истине»
Из беседы духа океана с духом реки в момент разлива реки.
3 , мерное комплексное евклидово пространство.
.
Общий вид задания скалярного произведения в
Рассмотрим два
вектора
и
,
координаты
векторов комплексные числа.
,
Первое условие.
Так как, согласно первой аксиоме
,
то имеем следующие соотношения
,
,
, (
)
Следовательно,
,
т.е.
-
матрица экмитовая.
Здесь мы ввели обозначение звездочку * - это знак эрмитова сопряжения.
Второе условие. Так как, согласно четвертой аксиоме , то
Следовательно, матрица должна определять положительно-определенную полуторалинейную форму.
4
,
множество функций, определенных на
отрезке
.
,
т.е. пространство бесконечноменое.
Рассмотрим две функции
и
,
.
Определим скалярное произведение,
используя определенный интеграл
.
Это простейший случай задания.
В общем случае скалярное произведение имеет вид
,
где функция
положительна на отрезке
.
Эта функция называется функцией
распределения, или весовой функцией.
Все аксиомы выполнены.
Неравенство Коши
–Буняковского
:
Докажем неравенство для случая вещественного линейного пространства.
Рассмотрим векторы
и
и их линейную комбинацию
,
.
Имеем
Это неравенство принимает лишь неотрицательные значения при любом . Следовательно, дискриминант не может быть положительным:
.
Что и требовалось доказать.
Следствие. Из неравенства Коши – Буняковского следует неравенство
.
Извлекаем из этого выражения квадратный корень и получаем
, где
- длина вектора
.
Введем
, где
угол между векторами . Это можно сделать,
так как выполняется очевидное условие.
.
Определение.
Линейное пространство, в котором введена
длина вектора
,
называется нормированным пространством,
если выполнены три условия:
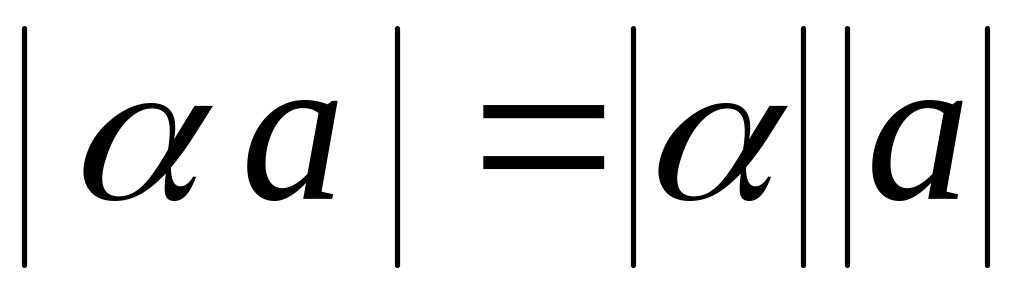
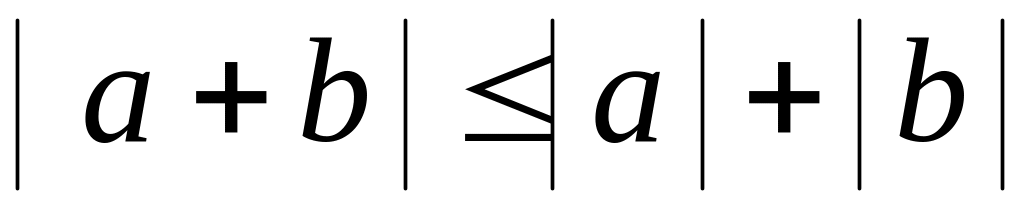- неравенство
треугольника.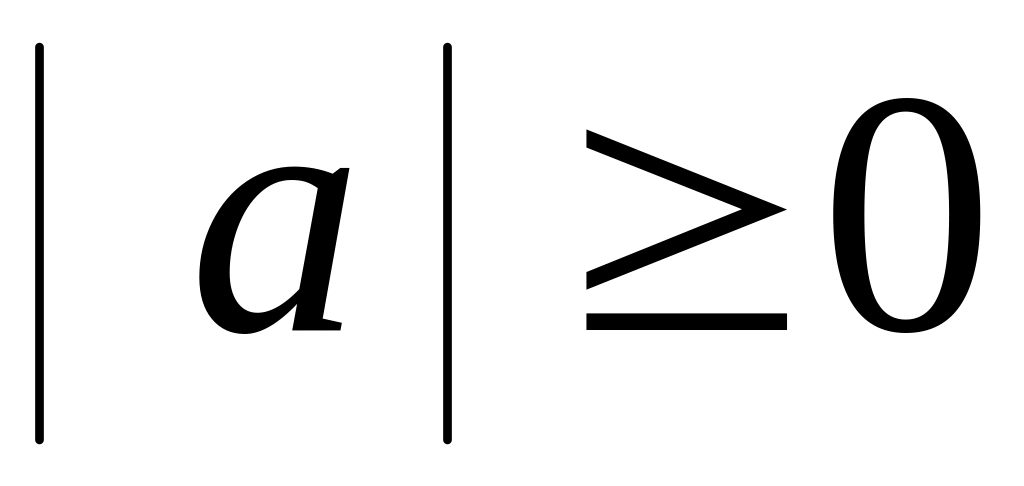
Любое евклидово пространство всегда является нормированным пространством, так как длину вектора всегда можно определить как квадратный корень из скалярного произведения . При этом все три условия выполняются. Чтобы убедиться в этом, решите следующую задачу.
Задача. Доказать неравенство треугольника, используя неравенство Коши_Буняковского
Лекция 10 лекция 11
Инвариантное подпространство. Собственный вектор и собственное значение линейного оператора. Характеристическое уравнение. Структура линейного оператора. Спектр линейного оператора.
-
«Право на левой стороне»
Инвариантное подпространство. Собственный вектор и собственное значение линейного оператора. Характеристическое уравнение. Структура линейного оператора.
Поставим следующий вопрос: Как, и каким образом, мы можем изучить устройство или структуру линейного оператора?
Ответ:
структура
линейного оператора полностью определяется
структурой
(или видом) матрицы линейного оператора.
Речь идет о
приведение матрицы
линейного оператора
к наиболее простому виду при
помощи выбора базиса.
Очевидно, наиболее простой матрицей
является диагональная матрица. Возникает
вопрос, как найти этот базис?
Центральное
место в решении этой задачи занимает
понятие инвариантного
подпространства,
в особенности, одномерного
инвариантного подпространства.
Интересная
и плодотворная картина структуры
линейного оператора возникает для
случая, когда линейный оператор производит
отображение линейного пространства в
себя
.
Итак,
рассмотрим в линейном пространстве
некоторое подпространство
,
.
Пусть
линейный оператор, действующий в
.
Определение.
Пусть
линейный оператор в
.
Подпространство
называется
инвариантным
относительно действия оператора
,
если для каждого вектора
из
вектор
также принадлежит
.
Или:
Подпространство
инвариантно
относительно действия оператора
,
если
Примеры инвариантных подпространств.
1.Нульмерное
пространство (пространство, состоящее
из нулевого вектора Пусть
и
.
2.Все пространство
:
и
.
3. Ядро линейного
оператора
:
и
.
4. Образ линейного
оператора
:
и
.
Особую роль играют одномерные инвариантные подпространства в .
Пусть
- одномерное инвариантное подпространство.
В силу одномерности
,
очевидно, что вектор
пропорционален
для каждого вектора
:
,
где
-
коэффициент пропорциональности.
Определение.
Вектор
,
удовлетворяющий соотношению
,
называется собственным вектором, а
число
-
собственным значением линейного
оператора
.
Итак, если
- собственный вектор, то векторы
образуют одномерное инвариантное
подпространство (линейная оболочка).
Обратно, любой вектор одномерного
инвариантного подпространства является
собственным вектором.
Зададим вопрос: Может ли существовать собственный вектор линейного оператора? Ответ дает следующая теорема.
ТЕОРЕМА. Всякий линейный оператор имеет, по крайней мере, один собственный вектор.
Доказательство. Предположим, что существует вектор : .
Выберем в
базис
.
Линейному оператору
в этом базисе соответствует некоторая
матрица
:
.
Тогда операторному соотношению
будет соответствовать матричное
соотношение:
,
или
,
(перенос правой
части налево:
или
).
В результате мы получили следующую систему однородных уравнений:
(1)
Данная система уравнений имеет неизвестных: среди них - неизвестных и число . Следовательно, для нахождения решения этой системы уравнений, необходимо еще одно уравнение, чтобы число неизвестных сравнялось с числом уравнений!
Мы знаем, что
однородная система уравнений имеет
нетривиальное решение
,
если
меньше
.
Это условие можно записать в виде условия
на определитель матрицы
:
Мы получили уравнение степени относительно . Это уравнение называется характеристическим или вековым уравнением. Вот мы и получили недостающее -ое уравнение.
Это уравнение
имеет, по крайней мере, один корень
.
Подставив в систему (1) вместо
корень
,
мы получим однородную систему уравнений,
определитель которой равен нулю, и
имеющую, следовательно, ненулевое
решение:
.
Тогда вектор
будет собственным вектором, а
собственным значением линейного
оператора
,
так как
Теорема доказана.
Характеристический
полином
.
Дадим следующее определение:
.
Очевидно, что
.
Спектр линейного оператора. Преобразование матрицы линейного оператора. Подобные матрицы.
Следствие теоремы.
Согласно основной теореме алгебры,
всякое уравнение
-ой степени имеет ровно
корней. Следовательно, характеристическое
уравнение
имеет
корней
.
Определение. Множество собственных значений линейного оператора называется спектром линейного оператора.
Спектр линейного оператора не зависит от выбора базиса. Ниже мы докажем это свойство.
Рассмотрим в линейном пространстве некоторый линейный оператор .
Выберем в два базиса:
В базисе линейному оператору соответствует матрица : .
В базисе
оператору
будет
соответствовать некоторая матрица
:
.
Итак
ТЕОРЕМА.
Матрицы
и
связаны соотношением
,
где
-
матрица перехода от базиса
к базису
.
Доказательство.
Итак,
или
.
Рассмотрим следующее выражение:
С другой стороны:
Сравнивая
эти два соотношения, получаем
В матричном виде это равенство имеет следующий вид:
или
Теорема доказана.
Определение.
Матрицы
и
называются подобными,
если существует невырожденная матрица
и
выполняется
.