Мир не линеен и поэтому сложен.

Функция. Когда мы говорим о функции, всегда подразумеваем следующую запись:

, где

Функция – это всегда отображение одного множества в другое множество. Следовательно, задать функцию можно с помощью задания отображения.

ОПРЕДЕЛЕНИЕ: Если для каждого элемента , принадлежащего множеству , поставлен в соответствие некоторый элемент , принадлежащий множеству , то говорят, что на множестве задана некоторая функция со значениями на множестве .

Символически это можно записать так .

Или, , то существует .

Итак, функция задана, если множество отображается в множество посредством .

Функция

В математике исторически сложились синонимы понятия функция:

Греция, 3 век до р.х. Легенда.

Вызвал к себе царь Евклида, написавшего 15 книг по математике и говорит:

“Слушай, разве подобает мне, царю, изучать все эти 15 книг. Как царь, я должен знать геометрию, но твой путь очень длинен для меня. Я повелеваю тебе указать в изучении геометрии Царский путь, более короткий для меня”.

Евклид ответил: “К сожалению, в науке нет царских путей. Как все смертные,

ты царь, если хочешь постичь геометрию, должен пройти

весь длинный путь, указанный мной в «Началах геометрии»”.

Лекции, семинары, изучение теории, решение задач и самостоятельная работа – вот путь студента в университете.

Матрицы и операции над матрицами.

ОПРЕДЕЛЕНИЕ: Прямоугольная таблица чисел , состоящая из - строк и - столбцов, называется матрицей порядка .

Матрица , в которой - строк и – столбцов с элементами :

- элемент матрицы, .

Матрицами порядка являются строки Матрицами порядка являются столбцы

В дальнейшем, как правило, мы будем иметь дело с матрицами порядка , т.е. квадратными матрицами -го порядка.

Примеры простейших матриц: нулевая , единичная , диагональная, треугольная, блочная и т.д.

Задание – запишите примеры этих матриц.

При введении обычных операций сложения и произведения матриц исходят из следующего основного требования – результат сложения и произведения матриц должен быть матрицей. При этом необходимо учитывать, что не всякие матрицы можно сложить и перемножить между собой, т.е. имеются ряд ограничений. Например, сложение определено для матриц одинакового порядка, произведение двух матриц определено для случая, когда количество столбцов первой матрицы равно количеству строк второй матрицы. В линейной алгебре, кроме обычных операций сложения матриц, произведения матриц, произведения матрицы на число, вводятся и другие очень важные операции: транспонирование; прямая сумма; след матрицы; определитель матрицы; нахождение обратной матрицы; эрмитово сопряжение и др.

Операции над матрицами.

• Сложение матриц порядка :

, где

Свойства операции сложения:

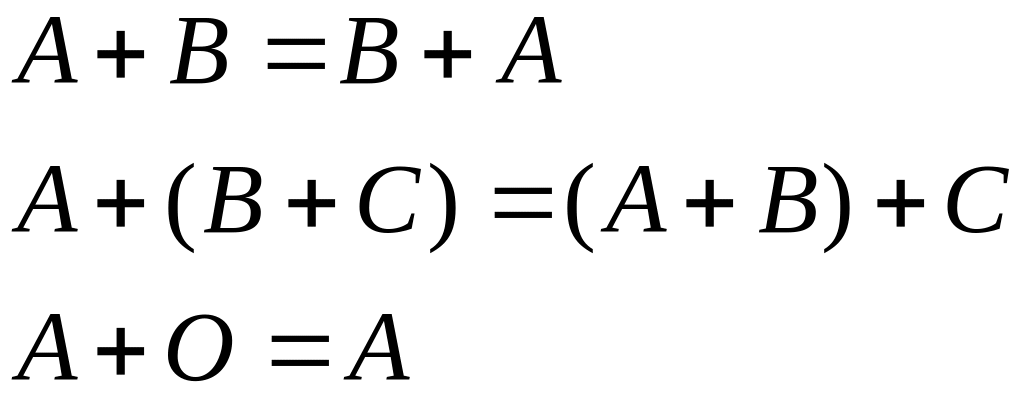
• Умножение матрицы на число:

, где

Свойства операции умножения:

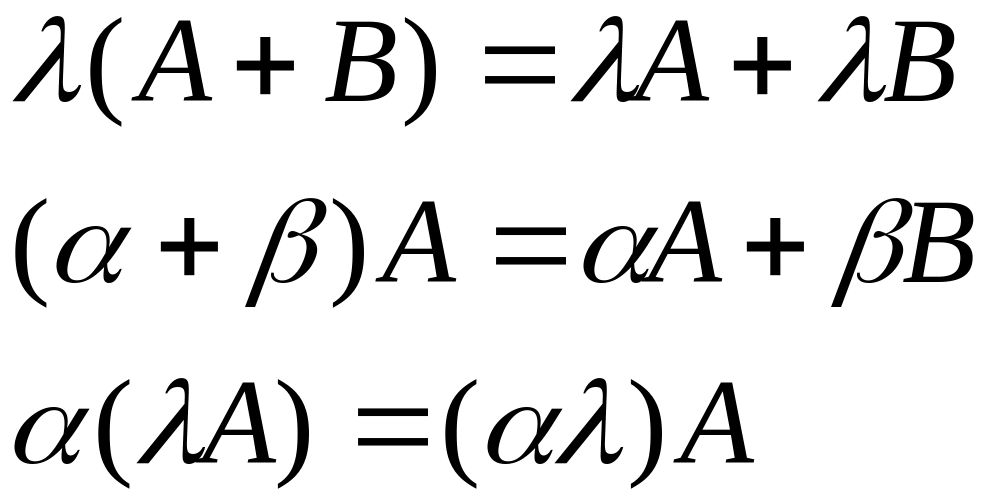
• Произведение матриц и ,

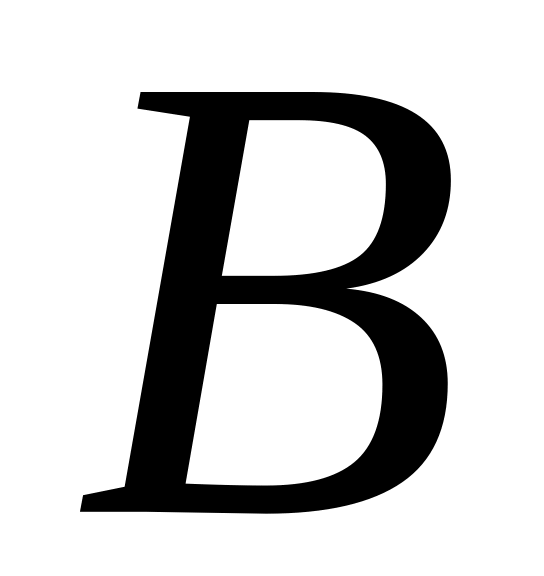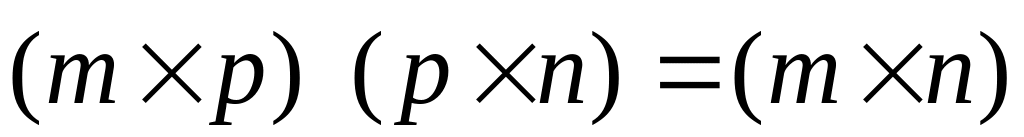
, где элементы матрицы :

Это правило «читается» следующим образом: элемент равен сумме произведений элементов ой строки первой матрицы умноженныt на элементы го столбца второй матрицы.

Очевидно, что произведение матриц не коммутативно. В общем случае . Если , то говорят, что матрицы и коммутативны. Произведение матриц ассоциативно и дистрибутивно (см. ниже свойства).

Свойства операции произведения:

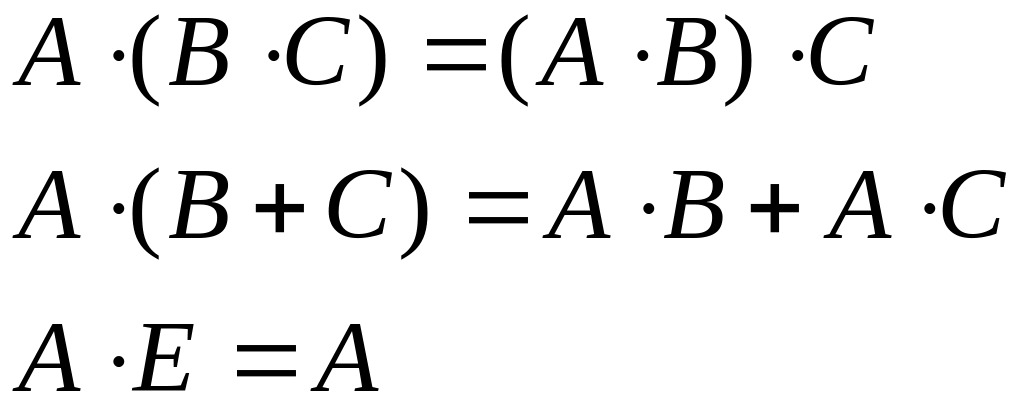
Для квадратных матриц можно определить такие операции произведения, как произведение Ли и произведение Иордана:

- произведение Ли, или коммутатор.

- произведение Иордана, антикоммутатор

• Транспонирование.

Рассмотрим матрицу . Выполним над строками матрицы следующую операцию транспонирования – строки матрицы запишем столбами некоторой матрицы , которую назовем транспонированной, по отношению к матрице :

, .

Символ , стоящий над матрицей справа, указывает на выполнение над матрицей операции транспонирования, или просто, ее транспонирование. Транспонирование можно применять к матрицам любого порядка.

Свойства операции транспонирования:

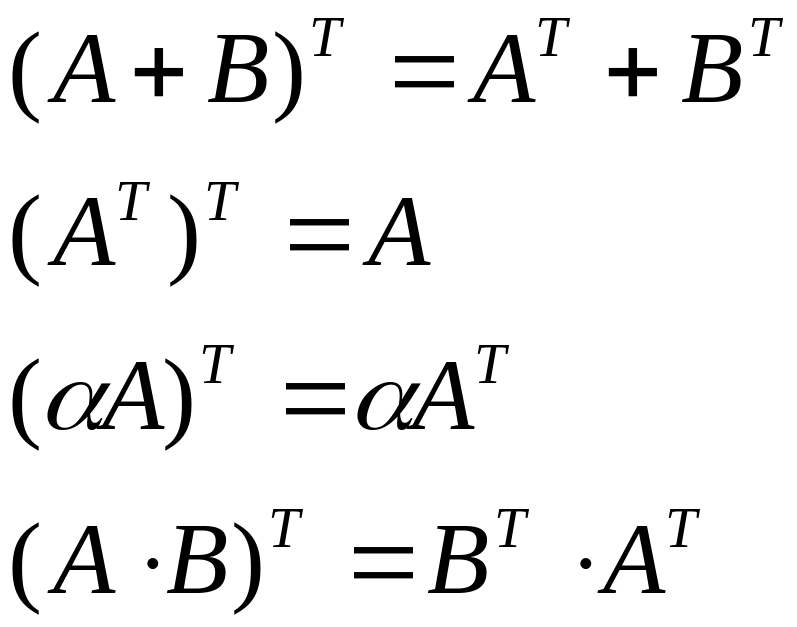
Для квадратных матриц выполняется ряд свойств. Пусть матрица и ее транспонированная совпадают, . Такая матрица называется симметричной. Элементы симметричной матрицы, расположенные симметрично относительно главной диагонали, равны между собой т.е. .

Если матрица противоположна своей транспонированной, , то такая матрица называется антисимметричной (другое название -кососимметричной). Элементы антисимметричной матрицы, расположенные симметрично относительно главной диагонали, противоположны , а элементы главной диагонали равны нулю .

Задача 1. Докажите свойство .

Задача 2. Докажите, что всякую квадратную матрицу можно представить в виде суммы симметричной и антисимметричной матрицы: , где - симметричная матрица, -антисимметричная матрицаэ

Задача 3. Докажите, что всякую функцию можно представить в виде суммы четной и нечетной функций.

• След матрицы. Введем еще одну числовую функцию – след матрицы. Обозначается след матрицы символом .

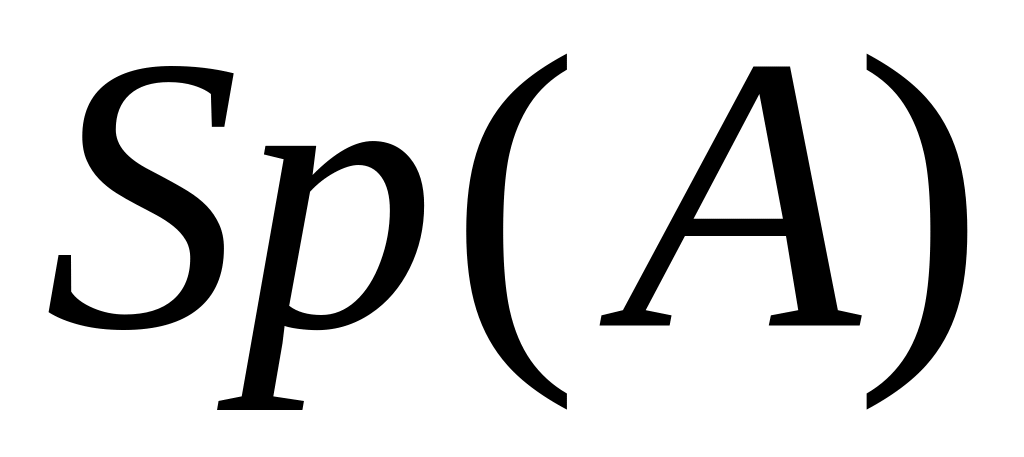Определение. Сумма диагональных элементов квадратной матрицы называется следом матрицы:

Свойства следа произведения матриц:

• Прямая сумма матриц.

Рассмотрим матрицы и порядка . Определим прямую сумму этих матриц. Прямая сумма обозначается символом - знак сложения в круге.

Итак: , где матрица имеет следующий вид

.

Следовательно, матрица будет иметь порядок . Очевидно,

,

т.е., результат вычисления прямой суммы зависит от порядка следования матриц и при сложении. Таким образом, операция вычисления прямой суммы не перестановочна (не коммутативна).

Следует отметить, что матрица имеет блочную структуру, в данном случае матрица имеет блочно-диагональный вид: по главной диагонали расположены матрицы и , а по второстепенной (не главной) – нулевые матрицы .

ЛЕКЦИЯ 2

Определитель матрицы. Минор и алгебраическое дополнение. Теорема 1. Лапласа, Теорема 2. О . Обратная матрица.

“Можно понять математику, когда она есть, но из понятия математика не вытекает ни одно математическое понятие”

Определитель матрицы.

Каждой квадратной матрице можно поставить в соответствие некоторое число, называемое определителем матрицы и обозначаемое символом .Следовательно, на множестве квадратных матриц мы можем задать числовую функцию. Символически числовая функция записывается так:

,

где - множество квадратных матриц порядка . Заметим, что у прямоугольных матриц определитель не существует (определить невозможно).

ОПРЕДЕЛЕНИЕ: Определителем матрицы называется число, которое сопоставляется каждой матрице по некоторому правилу вычисления.

Существуют два правила вычисления определителя матрицы.

1-ое правило вычисления.

Рассмотрим квадратную матрицу порядка с элементами . Правило вычисления определителя матрицы при разложении по 1-ой строке имеет вид:

.

При разложении по -ой строке:

Разложение по j-ому столбцу:

Таким образом, вычислять определитель можно путем разложения, как по строкам, так и по столбцам.

В формуле вычисления определителя величина называется минором с чертой элемента . Минор с чертой это определитель матрицы , у которой вычеркнуты (т.е. удалены) -ая строка и -ый столбец.

Введем величину . Эта величина называется алгебраическим дополнением элемента . Определитель матрицы можно записать через алгебраическое дополнение:

Пример определителя матрицы 2-го порядка:

2-ое правило вычисления.

Суммирование проводится по всем индексам от 1 до , причем индексы не должны совпадать ( -кратная сумма). Комбинация индексов в величине считается начальной комбинацией, для которой . Все остальные комбинации индексов получаются из начальной путем перестановки индексов, причем при четном числе перестановок величина , при нечетном - .

Для матрицы 3-го порядка определитель равен

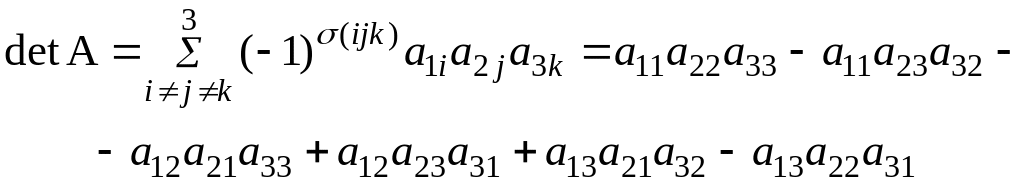
ОПРЕДЕЛЕНИЕ: Матрица , у которой называется вырожденной. Если , то называется невырожденной.

Рассмотрим миноры 2-х типов - миноры с чертой и миноры без черты.

Минор с чертой: - это определитель матрицы , у которой вычеркнуты строки и столбцы .

Минор без черты: - это определитель матрицы, составленной из элементов матрицы , стоящих на пересечении строк и столбцов .

Здесь индекс .

ТЕОРЕМА 1. Лапласа (1749-1827). Для любых строк и столбцов (причем ) имеем

Теорема без доказательства.

Свойства определителей.