
- •Лекция 1
- •Мир не линеен и поэтому сложен.
- •Основное свойство:
- •Линейное свойство:
- •Лекция 3
- •Лекция 4
- •Лекция 6 лекция 7
- •Лекция 8
- •Лекция 9
- •Лекция 10 лекция 11
- •Свойства подобных матриц.
- •Лекция 12
- •Лекция 13 лекция 14
- •Лекция 15
- •Лекция 16
- •Программа по линейной алгебре для студентов 1 курса физического факультета
- •I. Матрицы и определители
- •II. Линейные пространства
- •III. Системы линейных уравнений
- •IV. Евклидовы и унитарные пространства.
- •V. Линейные операторы в конечномерном пространстве.
- •VI. Билинейные и квадратичные формы. Функции от матриц.
- •Д.К.Фаддеев ”Лекции по алгебре” 2005г.
- •1. Проскуряков м.В.: - Сборник задач по линейной алгебре
- •2.Фаддеев д.К., Соминский и.С.: - Задачи по высшей алгебре
Лекция 1
Программа. Учебная литература. Что изучает алгебра? Линейность. Функция. Матрицы и операции над матрицами.
Программа курса Линейная алгебра
Матрицы и определители;
Линейное пространство;
Системы линейных уравнений;
Евклидовы пространства;
Линейные операторы;
Билинейные и квадратичные формы;
Функции от матриц;
-
“Понятие числа предполагает понятие множества и порядка. Поэтому человек, конечное существо, постигая мир, приобщается к бесконечно полной информации”
М.К.Мамардашвили
Учебная литература
Ильин В.А., Позняк Э.Г.: - “Линейная алгебра”
Федорчук В.В.: - “Курс аналитической геометрии и линей ной алгебры”
Канатников А.Н., Крищенко А.П.: - Линейная алгебра, 1998г. Изд. МВТУ им. Баумана
Ефимов Н.В., Розендорн Э.Р.: - Линейная алгебра и многомерная геометрия
Гельфанд И.М.: - “Лекции по линейной алгебре”
Александров П.С.: - “Курс аналитической геометрии и высшей алгебры”
Курош А.Г.: - “Курс высшей алгебры”
Шилов Г.Е.: - “Конечномерные линейные пространства”
Бугров, Никольский: - Элементы линейной алгебры и аналитической геометрии
Беклемишев Д.В.: - “Курс аналитической геометрии и высшей алгебры”
Кострикин А.И., Манин Ю.М.: - “Линейная алгебра”. Изд. МГУ
Гантмахер Ф.Э.: - “Теория матриц”
Фаддеев Д.К. : -”Лекции по алгебре”, 2005г.
Сборники задач
Проскуряков М.В. : - Сборник задач по линейной алгебре
Фаддеев Д.К., Соминский И.С. : - Задачи по высшей алгебре
Примечание: жирным шрифтом выделены основные учебники.
Что изучает алгебра! Линейность. Функция.
Множества, изучаемые в математике.
-
Числовые множества:
 - Натуральные
числа
- Натуральные
числа - Целые числа
- Целые числа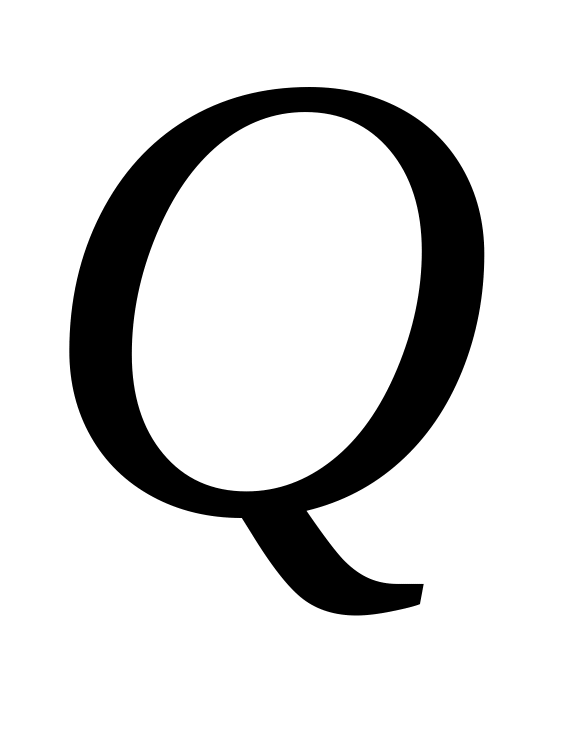 - Рациональные
числа
- Рациональные
числа - Вещественные
числа
- Вещественные
числа- Комплексные числа:

- Кватернионы:

где

Октавы: …………
Другие множества:
Функции:

Векторы:

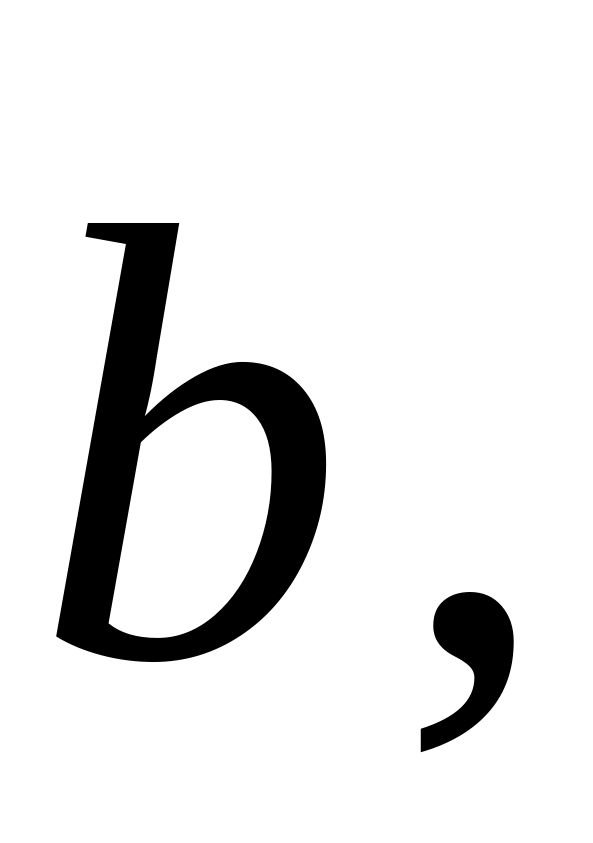 ….
….Матрицы:
 ,…
,…
Операторы:
 ,…
,…Тензоры:

 ….
….Спиноры:
 ….
….
«Когда на вопрос, что изучает математика, отвечают: множества с заданными в них отношениями, то это вряд ли можно признать ответом. Ведь среди континуума мыслимых множеств с заданными в них отношениями, или структур, математиков реально привлекает редкое, дискретное множество. И смысл вопроса заключается в том, чтобы понять, чем же особенно ценна эта исчезающе малая часть, вкрапленная в аморфную массу.
… Точно также, смысл любого математического понятия лишь в малой степени содержится в его формальном определении. Не меньше, скорее больше, дает набор основных примеров, являющихся, одновременно, и мотивировкой, и содержательным определением и смыслом понятия».
И.Р.Шафаревич, академик РАН
Линейная алгебра базируется на аксиоматическом методе, согласно которому вводятся первичные, неопределяемые понятия, подчиняющиеся некоторому набору аксиом. В элементарной геометрии первичными понятиями являются точка, прямая и плоскость, а аксиомами являются, например, следующие утверждения:
- каковы бы ни были две точки А и В, существует прямая, которой принадлежат две эти точки (через две точки проходит прямая, и притом только одна);
- в плоскости, определяемой точкой А и прямой L существует не более одной прямой, проходящей через А и не пересекающей L (через одну точку можно провести единственную прямую, параллельную данной).
Аксиомы – это первичные утверждения, которые считаются верными изначально. Аксиоматический метод позволяет все утверждения теории выводить из заданных аксиом. Доказательство утверждений проводится более строго, но и более формально. В результате линейная алгебра, в отличие от геометрии, становится менее наглядной и более сложной для восприятия. Однако трудности изучения линейной алгебры окупаются возможностью увидеть и установить связи между различными разделами математики. Это приводит к фундаментальным понятиям математики и формирует единство ее логических принципов.
Линейность. В физике основные принципы и законы выражаются на языке математики в виде линейных конструкций. Почти всякий естественный процесс, и физический в том числе, почти всюду, в малом, линеен. С более общей точки зрения, содержание линейной алгебры состоит в разработке математического языка для выражения одной из самых общих естественнонаучных идей – идеи линейности.
Например, эффективность применения дифференциального исчисления для описания многих физических и механических явлений, связана с тем, что малые приращения некоторых двух физических величин между собой пропорциональны:
![]() ,
,
где
![]() и
и
![]() физические величины,
физические величины,
![]() коэффициент пропорциональности
(производная).
коэффициент пропорциональности
(производная).
Квантовая физика XX века резко расширила сферу применения идеи линейности, добавив к принципу линейности малых приращений принцип суперпозиции векторов состояний. В результате линейная алгебра превратилась в аппарат, используемый для формулировки фундаментальных физических законов природы, например, объясняющих таблицу Менделеева, систематику элементарных частиц и даже свойства пространства-времени.
Однако, все сложнее. Окружающий нас мир природы не всегда допускает линейные способы и модели описания явлений. Мир полон как линейными, так и нелинейными явлениями.
