
- •I. Алгебраические основы теории циклических кодов
- •1.2. Поля Галуа и их свойства
- •1.3. Основные действия над многочленами в поле двоичных чисел и их реализация
- •1. Сложение многочленов
- •2. Умножение многочленов
- •3. Деление многочленов
- •4. Реализация операций умножения и деления многочленов в поле двоичных чисел
- •4. Циклические коды, исправляющие пачки ошибок (коды файра)
- •5. Циклические коды бчх
- •6. Циклические коды рида—соломона
- •6.2 Построение кодов Рида-Соломона
- •6.3. Использование кодов Рида—Соломона для исправления стираний
- •6.4. Реализация действий над элементами поля
- •7. Мажоритарное декодирование циклических кодов
- •1.Алгебраические основы теории циклических кодов 2
- •Определение группы, кольца, поля
6.3. Использование кодов Рида—Соломона для исправления стираний
Код Рида—Соломона с минимальным расстоянием d может исправлять d—1 или менее стираний. При этом под стиранием понимается такое состояние приемника, когда значение сигнала попадает в так называемую зону неопределенности. Для каскадных кодов под стиранием понимают «маскирование». Это означает, что на предшествующем уровне декодирования применяют код, обнаруживающий ошибки, что позволяет пометить специальным образом элементы кодовых комбинаций с обнаруженными ошибками. Таким образом, при передаче кодового вектора по стирающему каналу на приемной стороне становятся известными номера позиций Х1,X2, ..., Xt со стираниями пли отмеченные специальной «маской». Поэтому задачей декодирования является определение неизвестных кодовых элементов, расположенных на этих позициях. Алгоритм исправления стираний мало чем отличается от исправления ошибок и сводится к решению системы уравнений (6.8) относительно неизвестных Yt, которые являются значениями стертых символов комбинации либо значениями вектора ошибок в позициях, помеченных «масками».
Рассмотрим пример исправления стираний. Пусть (п, k)— код Рида—Соломона с образующим полиномом g(x) = (х+ 1)(x+ а) имеет минимальное расстояние d = 3. Тогда такой код исправляет одно или два стирания. Проверочная матрица имеет вид (6.17).
Пусть далее, а — примитивный элемент поля GF (23) с порождающим полиномом Р (х) = 1 + х+x3. Тогда, выбрав длину комбинации n = 23—1, мы построим код (7, 5), который может исправлять одно или два стирания или однократную ошибку без стираний.
Рассмотрим передачу по стирающему каналу кодового век-гора
(c0c1c2c3c4c5c6)=(a61aa2a3a4a5),
где элементы сi являются коэффициентами разрешенной кодовой комбинации кода (7, 5), представленной полиномом (6.1). Предположим, что в результате приема имели место два стирания и были стерты элементы c2 и с4 и тогда на декодер поступит комбинация (а6 1 0 а2 0 а4 а5). Таким образом стертые позиции Х1 = х2 и Х2 = х4 известны. Умножив принятый вектор со стираниями на НT в соответствии с (6.17), получим значения синдромов
S0=Y1+Y2=1
S1=Y1X1+Y2X2=a
Решая полученную систему уравнений относительно значений стертых символов Y1 и Y2 находим:
Y2=S0+Y1=a3.
Таким образом, зная номера X1 и X2 стертых символов, может быть осуществлено исправление стираний путем замены, нулей найденными значениями Y1 и Y2.
6.4. Реализация действий над элементами поля
При построении кодирующих и декодирующих устройств циклических кодов, особенно БЧХ и Рида—Соломона, должны быть реализованы операции умножения и деления в поле GF(2k). Рассмотрим реализационные основы таких действий над элементами конечного поля Галуа.
 Пусть
задан примитивный полином k-й
степени
над простым
полем GF
(2):
Пусть
задан примитивный полином k-й
степени
над простым
полем GF
(2):
Квадратной матрице F соответствует характеристический полином f (λ), представляющий собой определитель характеристической матрицы [λЕ— F], где Е — квадратная единичная матрица k-го порядка, т. е. f (λ) =│ λ Е— F│. Корни полинома f (λ ) λ 1, λ 2, … λ k, называемые характеристическими числами, являются решением векового [9] уравнения │ λ Е— F│ = 0.
Как видно из этого уравнения, одним из корней полинома f (λ ) является сопровождающая матрица F. Действительно, если в характеристический полином f (λ ) вместо λ подставить F, то получим f (F) = │FE — F│ =0, Тем самым доказана теорема Гамильтона—Кэли [9], в соответствии с которой всякая квадратная матрица F является корнем своего характеристического полинома f (λ ).
С другой стороны, легко проверить, что заданный примитивный полином Р (х) в точности совпадает с характеристическим полиномом f(X) при подстановке х = λ , т. е. f (λ ) = Р (λ ). Отсюда следует, что матрица F является также корнем полинома Р (х), т. е. Р (F) = 0. Последнее условие приводит к важному следствию, заключающемуся в том, что множество элементов поля GF(2k) построенного по примитивному полиному Р (х), изоморфно множеству полиномов — вычетов по модулю P(F). Другими словами, любому элементу am поля GF(2k), выраженному через степенной базис
![]()
где.
а — первообразный элемент поля, а
коэффициенты а,
eGF(2),
взаимнооднозначно соответствует
многочлен
приведенный по модулю Р (F). Указанное свойство позволяет достаточно просто реализовать умножение и деление элементов поля GF (2к) в векторной форме. Рассмотрим эти действия.
6.4.1. Умножение элементов поля
 Пусть
необходимо умножить элемент аi
на элемент aJ.
С
этой целью выразим эти элементы поля
GF
(2k)
через степенной базис следующим
образом:
Пусть
необходимо умножить элемент аi
на элемент aJ.
С
этой целью выразим эти элементы поля
GF
(2k)
через степенной базис следующим
образом:
(a0a1…ak)Fj=(a0a1…ak)[b0E+b1F+…bk-1Fk-1]=

Напомним, что для двоичных кодов сложение производится по mod 2.
Структурная схема умножителя в соответствии с алгоритмом (6.24) представлена на рис. 6.8.

Рис. 6.8. Структурная схема умножителя произвольных элементов поля GF(2k)
Рассмотрим конкретный пример.
 Пусть
поле GF
(24)
образовано примитивным полиномом Р
(х) =
1+x+x4.
Сопровождающая
матрица F
этого
полинома
и ее степени F2
и
F3
имеют вид
Пусть
поле GF
(24)
образовано примитивным полиномом Р
(х) =
1+x+x4.
Сопровождающая
матрица F
этого
полинома
и ее степени F2
и
F3
имеют вид
Выразим аi и аj через базис {1, а, а2, а3} следующим образом:
![]()
Таким образом, векторная форма записи элементов аi и аj будет соответственно [а] = [а0, аь а2, a3] и [b] = [bо, b1, b2, b3]. Заменив элемент поля aJ на Fj, равный Fj=b0E+b1F+b2F2+b3F3, найдем произведение (aiaj )= со +c1a+c2a2+c3a3 в векторной форме, используя алгоритм (6.24), а именно
![]()
У чтем,
что для данного полинома Р
(х) и
его матрицы F
имеют
место равенства:
чтем,
что для данного полинома Р
(х) и
его матрицы F
имеют
место равенства:
Тогда вектор [c]=[c0,c1,c2,c3], соответствующий произведению aiaj, будет равен поэлементной сумме по модулю два
Ф![]()
 ункциональная
схема существенно упрощается, если
необходимо произвольный элемент поля
ai
умножить на константу aj.
Пусть для рассматриваемого выше примера
необходимо производить умножение на
а5.
Тогда произведение аia5
в векторной форме будет выражаться
следующим образом:
ункциональная
схема существенно упрощается, если
необходимо произвольный элемент поля
ai
умножить на константу aj.
Пусть для рассматриваемого выше примера
необходимо производить умножение на
а5.
Тогда произведение аia5
в векторной форме будет выражаться
следующим образом:
Функциональная схема такого умножителя представлена на рис. 6.10.

Рис 6.9. Функциональная схема умножения произвольных элементов поля GF (24) с образующим многочленом Р(х) = 1 + х + х4
Другой распространенный в настоящее время алгоритм умножения элементов поля GF (2k) основан на применении операций логарифмирования и антилогарифмирования в полях GF (2k) [4, 6].
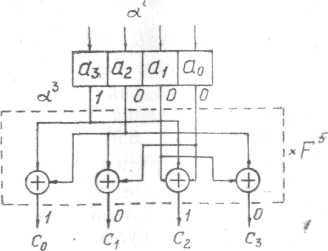
Рис. 6.10. Функциональная схема умножения произвольного элемента аi поля GF(24) на константу a5
Если некоторый элемент поля β=ai принадлежит полю GF(2k), то логарифм элемента β по основанию a€GF (2k) есть показатель степени i, а именно: Log β = log ai=i, i≥0. Тогда, умножение aiaj= am может быть реализовано по следующему алгоритму, представленному на рис. 6.11.

Особенностью данного алгоритма является то, что комбинациям из k нулей или k единиц на выходе арифметического сумматора должно соответствовать появление на выходе ан-тилогарифматора одинакового элемента, а именно а0 = 1.
Логарифмирование и антилогарифмирование реализуется чаще всего табличным способом.
6.4.2. Деление элементов поля
В теории циклических кодов часто встречающейся операцией является деление произвольного элемента ai на некоторый элемент aj, где ai , ai€GF (2k). Вместе с тем на практике деление элементов заменяется умножением элемента ai на a-j, т. е.
![]()
где a-j —элемент поля, обратный элементу аj. Напомним, что для любого элемента аj в поле GF (2k) всегда существует и обратный ему a-j , которые связаны равенством aja-j= 1. Таким образом, реализация деления осуществляется по той же схеме, что и умножение (рис. 6.9) с той разницей, что один из сомножителей является обратным элементом a-j. Рассмотрим способы обращения элементов поля GF(2k).
Один из способов основан на свойстве полей Галуа, которое заключается в том, что ненулевые элементы поля GF (2k) образуют циклическую мильтипликативную группу порядка 2k — 1, т. е. для любого ненулевого элемента аj справедливо
равенство (аj)2k-1 = 1. Отсюда получается (аj)2k-2 =
= (aJ)-1= a-j. Для вычисления (2k —2)-й степени элемента β можем воспользоваться одним из следующих двух равенств:

(β )2k-2={[(β2β)2β]2… β }2= β -1 (6.27)
Характерной особенностью равенства (6.26) является то, что обращение элемента β может быть реализовано аппаратным путем за один шаг (такт), тогда как равенство (6.27) может быть реализовано за (k—1) последовательных этапов. Вместе с тем реализация последнего значительно проще. На каждом этапе необходимо осуществить умножение текущего значения на β и возведение результата в квадрат. Если элемент β выразить через базисные элементы поля 1, а, а2, ..., аk-1 в виде β = а0 +a1a+a2a2+…ak-1ak-1, то на основании свойств (1.4) и (1.5) возведение в квадрат в поле GF (2*) соответствует выражению
![]()
Тогда операцию возведения в квадрат в векторной форме можно записать
(a0a1a2…ak-1)[X] = (b0b1b2…bk-1),
где [X] — квадратная матрица k-го порядка, строки которой представляют собой двоичные векторы элементов поля
![]()
Пример. Построить матрицу [X] и схему возведения в квадрат, если конечное поле GF (24) образовано примитивным полиномом Р (х) = 1+x+x4
Выразим элементы поля а0, а2, а4, а6 через базис {1, а, а2 а3} в виде аi = с0 + с1а + с2а2 + c3а3, где с€GF (2):

И з
векторов (с0 с1 с2 с3) указанных элементов
составим матрицу [X]:
з
векторов (с0 с1 с2 с3) указанных элементов
составим матрицу [X]:
Пусть элементу аi соответствует вектор (а0 а1 а2 а3). Для возведения аi в квадрат произведем умножение вектора (а0 а1 а2 а3) на матрицу [X]:

образующим полиномом Р(х) = 1 + х +x4 представлена на рис. 6.12.
Для проверки возведем элемент а5 в квадрат. Так как a5 = a +а2, то для получения элемента (а5)2 выполним умножение вектора элемента а5 на матрицу [X], т. е.


Рис. 6.12. Функциональная схема
возведения в квадрат произвольного элемента аi в поло GF(24)
Полученный вектор (1110) соответствует элементу (а5)2 = a10 поля GF (24).
