1.3. Основные действия над многочленами в поле двоичных чисел и их реализация

Условимся, что векторному представлению (а₀а₁.. а_п-2а_п-1) будет соответствовать многочлен f(х)= а₀ +а₁х+ ...+а_n-1x^n-1 , где коэффициенты a_i представляют собой наимень­шие неотрицательные вычеты по модулю р, т. е. принимают зна­чения 0, 1, 2, ... (р— 1). Для двоичных полей с характеристи­кой р = 2 коэффициенты a_i принимают значения 0 и 1.

Например, двоичной комбинации (101101) соответствует многочлен 1 + х² + x³+ x⁵

1. Сложение многочленов

Правило сложения многочленов сводится к суммированию коэффициентов при одинаковых степенях х и приведению сум­мы по модулю р.

((11) (1.2)

In

П усть

где коэффициенты а_i и b_i, принимают значения 0, 1, 2, ... (р— 1). Тогда сумма многочленов будет:

Очевидно, что сумма (a_i+b_i) сравнима с с_i по модулю р. т. е. (a_i+b_i)=(modp). Иногда просто говорят, что коэффи­циенты а_i и b_i складываются по модулю р. Пусть р = 3, а_i = 2иb_i= 2, тогда (а_i + b_i )=(2 + 2) = 4 = 1 (mod 3).

Ha основании этого сумма полиномов f_i(х) = 1 + х³ + х⁵ и f2 (х) =x+x³+х⁷с коэффициентами — вычетами по модулю 2 будет равна: f₁(х) +f₂ (х) = 1 +x + х⁵+x⁷

В дальнейшем мы будем рассматривать действия над эле­ментами двоичных полей, поэтому приведем правило сложения двоичных элементов по модулю 2:

1+1=0 0+1 = 1.

1+0=1. 0+0 = 0.

2. Умножение многочленов

Умножение многочленов осуществляется по обычным прави­лам перемножения. Пусть даны два многочлена (1.1) и (1.2), тогда произведение их будет равно:

Таким образом, коэффициент при хⁱ будет равен

Пример. Даны два многочлена с коэффициентами из двоич­ного поля:

Их произведение после приведения коэффициентов по моду­лю 2 будет равно: f₁(x)f₂ (х) = х + х⁶ + х⁹ +x¹⁰

3. Деление многочленов

Операция деления многочленов осуществляется по обычным правилам деления с приведением коэффициентов по mod р. На­пример, деление многочленов в двоичном поле (р = 2) осуще­ствляется следующим образом:

В общем виде эта операция может быть записана так:

При этом коэффициенты

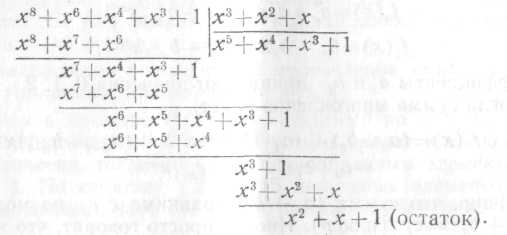
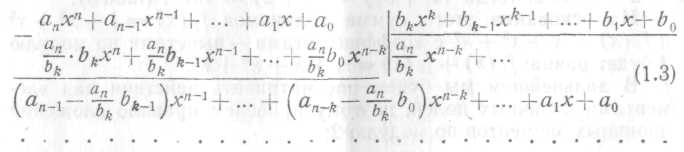
приводятся по модулю р. Для двоичных полей (р = 2) опера­ция вычитания равноценна операции сложения, так как —1 = 1 (mod2). Действительно, —1=-1+2= 1 (mod 2).

О перации сложения, деления и умножения многочленов мо­гут быть осуществлены над комбинациями коэффициентов этих многочленов. Пусть

Многочлену f₁(x) соответствует комбинация (100110101), а мно­гочлену f₂(x)—(0111). Начало комбинации соответствует младшему разряду, т. е. нулевой степени х.

а) сложение f₁(x) + f₂ (x):

б) умножение f₁(x)*f₂ (x):

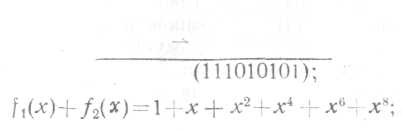
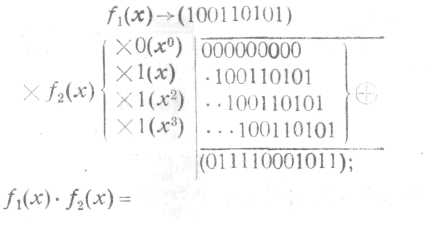
=x+x²+x³+x⁴+x⁸+x¹⁰+x¹¹

Таким образом, если начало комбинации f₁ (x) соответствует младшему разряду, т. е. х°, то умножению на хⁱ соответствует сдвиг комбинации f₁ (х) на число шагов, равное i. Полученный таким образом ряд комбинаций складывают по модулю 2. Как правило, нулевые комбинации (соответствующие умножению на 0) не записывают;

в) деление f₁ (х) :f₂ (х).

При делении комбинации f₁ (х) на f₂ (х) их записывают со стар­шего разряда и делят следующим образом: