
- •Эконометрическая модель.
- •Измерения в экономике. Шкалы измерений.
- •Случайные события и случайные переменные. Распределение случайных величин.
- •Статистические характеристики случайных величин и их свойства.
- •Основные функции распределения.
- •Оценки статистических характеристик и их желательные свойства. (нету)
- •Проверка статистических гипотез.
- •Критерий и критическая область.
- •Мощность статистического критерия. Уровень значимости.
- •Модель линейной регрессии.
- •Свойства оценок параметров, полученных методом наименьших квадратов. Условия Гаусса – Маркова.
- •Коэффициент детерминации и его свойства.
- •Предположение о нормальном распределении случайной ошибки в рамках классической линейной регрессии и его следствия.
- •Прогнозирование по регрессионной модели и его точность. Доверительные и интервалы прогноза (с лекции)
- •Ковариационная матрица оценок коэффициентов регрессии.
- •19. Проверка значимости коэффициентов и адекватности регрессии для множественной линейной регрессионной модели.
- •20. Коэффициент множественной детерминации. Скорректированный коэффициент детерминации.
- •21. Проблемы спецификации регрессионной модели. Пошаговая регрессия.
- •22. Замещающие переменные. Фиктивные переменные.
- •Методы борьбы с мультиколлинеарностью.
- •Линеаризация регрессионных моделей путем логарифмических преобразований.
Предположение о нормальном распределении случайной ошибки в рамках классической линейной регрессии и его следствия.
Предложение об ошибках в классической модели формируются наиболее жестким и не всегда реалистичным путем:
Предполагается,
что ошибка (![]() (
= 1 … N))
образует так называемый слабый белый
шум – последовательность центрированных
(
(
= 1 … N))
образует так называемый слабый белый
шум – последовательность центрированных
(![]() )
и не коррелированных случайных величин
с одинаковыми дисперсиями
)
и не коррелированных случайных величин
с одинаковыми дисперсиями
![]()
Свойство
центрированности практически не является
ограничением, так как при наличии
постоянного регрессора среднее значение
ошибки можно было бы включить в
соответствующий коэффициент (![]() )В
ряде случаев сделанные предложения об
ошибках будут дополняться свойствами
нормальности – случайный вектор
имеет нормальное распределение. Эту
модель мы будем называть классической
моделью с нормально распределительными
ошибками.
)В
ряде случаев сделанные предложения об
ошибках будут дополняться свойствами
нормальности – случайный вектор
имеет нормальное распределение. Эту
модель мы будем называть классической
моделью с нормально распределительными
ошибками.
Многомерное
нормальное распределение задается
своим вектором и матрицей ковариации
– здесь она имеет вид
![]() ,
где 1 – единичная матрица. Если компоненты
вектора корелированы, следовательно,
автоматически независимы, следовательно,
ошибки в модели образуют последовательность
независимых одинаково нормально
распределенных случайных величин N
(0;
,
где 1 – единичная матрица. Если компоненты
вектора корелированы, следовательно,
автоматически независимы, следовательно,
ошибки в модели образуют последовательность
независимых одинаково нормально
распределенных случайных величин N
(0;![]() ).Если
каждая из величин
нормально
распределена, то вектор ,
из них составленный, ну обязан быть
нормально распределенным.
).Если
каждая из величин
нормально
распределена, то вектор ,
из них составленный, ну обязан быть
нормально распределенным.
Доверительные интервалы оценок параметров и проверка гипотез об их значимости.
Доверительные интервалы параметров регрессии определяются следующим образом.
![]()
Здесь td - значение t-статистики для выбранного уровня значимости d. Величина p=1-d называется доверительной вероятностью или уровнем надежности, нередко выражаемым в процентах. Это показатель, характеризует вероятность того, что теоретическое значение параметра регрессии будет находиться в полученном доверительном интервале.
С лекции: =b0 – b1*X1 – это случайные величины, поэтому необходимо найти доверительные интервалы для истинных значений b0 и b1.
Bi принадлежит (bi +- дельта bi), где дельта bi = Sbi*tкрит
B0 принадлежит ( b0 +- Sb0 * t крит)
B1 принадлжет (b1 +- Sb1 * t крит)
Прогнозирование по регрессионной модели и его точность. Доверительные и интервалы прогноза (с лекции)
Мы получили регрессионную математическую модель и можем прогнозировать процесс путем вычислений. Основным фактором в прогнозировании чаще всего оказывается трендовая компонента. Он особен давать достаточно надежные прогнозы и на 4-5 шагов,следовательно,идёт расчет оценок среднесрочных и долгосрочных прогнозов.
Линейный
метод наименьших квадратов позволяет
по серии наблюдений Xi и Yi установить
параметры линейного уравнения вида
![]() где Yc,i –
расчетное значение отклика при заданном
моменте времени Xi, а b0 и b1 -
параметры линейной модели.
где Yc,i –
расчетное значение отклика при заданном
моменте времени Xi, а b0 и b1 -
параметры линейной модели.
Для оценки(проверки) прогноза возможны след способы: 1)По реальным прогнозируемым данным. 2)Построение точечного и интервального прогноза.
P (прогноз) = b0+b1*Xp
Дельта
(предельная
ошибка) = t
критич * S![]() р
р
Доверительный
интервал, учитывающий неопределенность,
связанную с положением тренда, и
возможность отклонения от этого тренда,
определяется в виде:
![]() где
n - длина временного ряда; L -период
упреждения; yn+L -точечный прогноз на
момент n+L; ta- значение t-статистики
Стьюдента; Sp- средняя квадратическая
ошибка прогноза. Предположим, что тренд
характеризуется прямой:
где
n - длина временного ряда; L -период
упреждения; yn+L -точечный прогноз на
момент n+L; ta- значение t-статистики
Стьюдента; Sp- средняя квадратическая
ошибка прогноза. Предположим, что тренд
характеризуется прямой:
![]() Так
как оценки параметров определяются по
выборочной совокупности, представленной
временным рядом, то они содержат
погрешность.
Так
как оценки параметров определяются по
выборочной совокупности, представленной
временным рядом, то они содержат
погрешность.
Тогда
доверительный интервал можно представить
в виде:
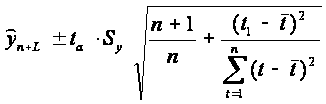
Дисперсия отклонений фактических наблюдений от расчетных определяется выражением:
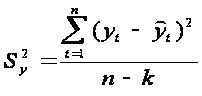 где yt-
фактические значения уровней ряда,
где yt-
фактические значения уровней ряда,
