10. Модель линейной регрессии.

Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретации ее параметров.

Функцией регрессии называется зависимость среднего значения одной из коррелированных случайных величин от другой, то есть функция: y = (x) (регрессия Y на X) или x = (y) (регрессия X на Y).

Линейная регрессия сводится к нахождению уравнения вида = a + b  x или y = a + b  x + . Это уравнение позволяет по заданным значениям фактора x иметь теоретические значения результативного признака подстановки в него фактических значений фактора x.

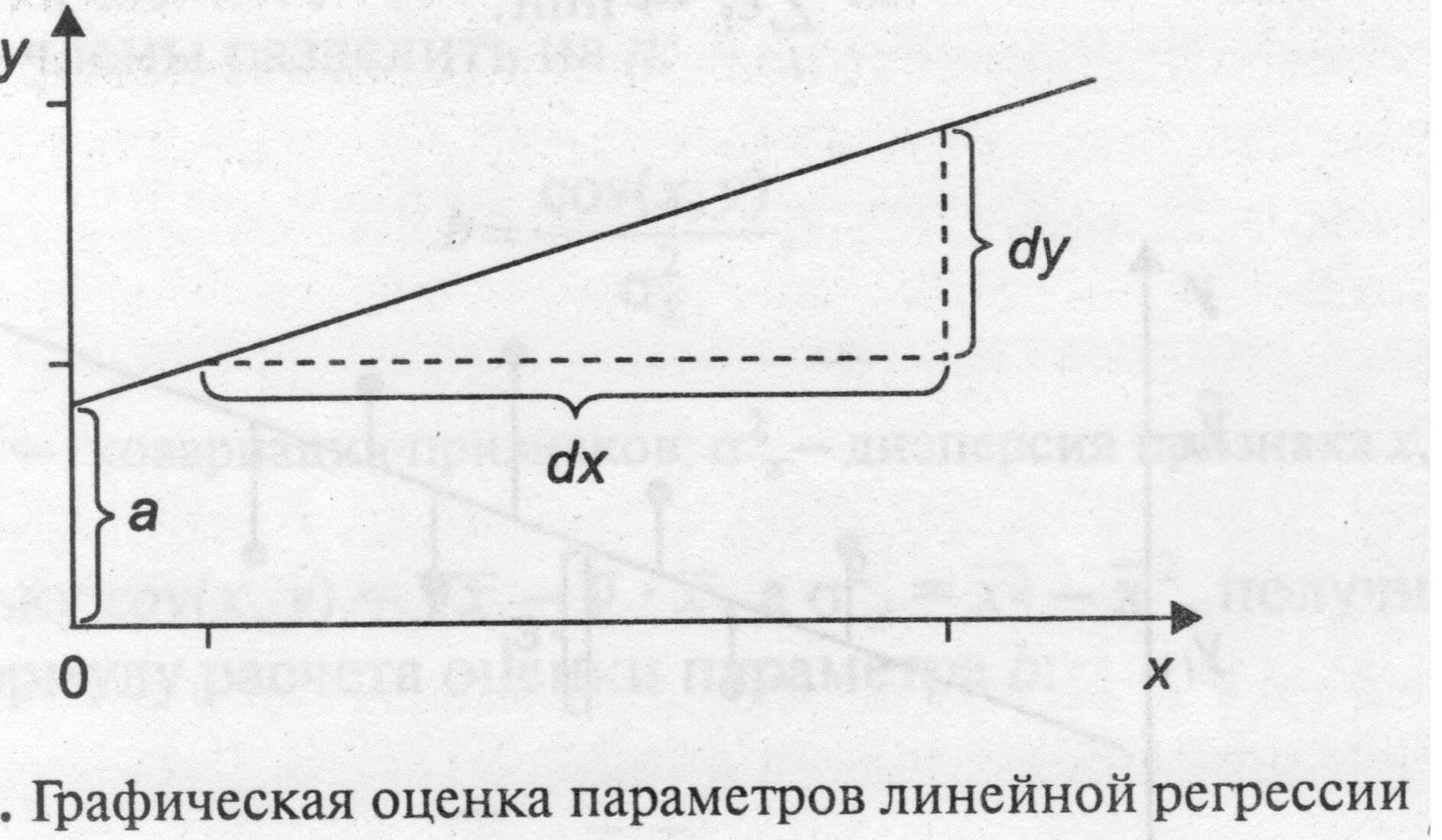
Построение линейной регрессии сводится к оценке ее параметров – a и b. Оценки параметров линейной регрессии могут быть найдены разными методами. Можно обратиться к полю корреляции и, выбрав на графике две точки, провести через них прямую линию, затем по графику найти значения параметров. Параметр a определим как точку пересечения линии регрессии с осью oy, а параметр b оценим исходя из угла наклона линии регрессии как dy/dx, где dy – приращение результата y, a dx – приращение фактора x, т.е. = a + b  x

11-12. Оценивание параметров регрессии. Метод наименьших квадратов.

Система уравнений МНК, её решение.

Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). При оценке параметров уравнения регрессии применяется МНК - это особая форма случайной величины, свойства которой зависят от свойств остаточного члена в уравнении.

МНК позволяет получить такие оценки параметров a и b, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) минимальна: .

Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной:

Для того чтобы найти минимум функции надо вычислить частные производные по каждому из параметров a и b и приравнять к нулю.

Обозначим через S, тогда:

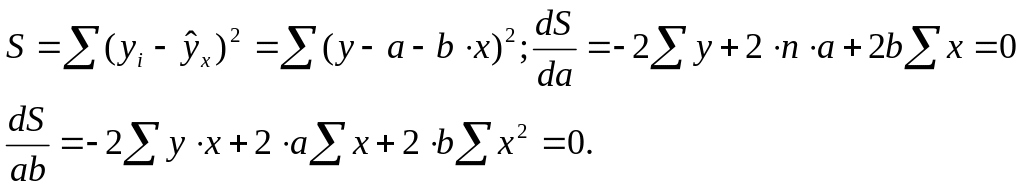
Преобразую формулу, получим следующую систему нормальных уравнений для оценки параметров a и b:

(система нормальных уравнений)

Решая систему нормальных уравнений либо методом последовательного исключения переменных, либо методом определителей, найдем искомые оценки параметров a и b. Можно воспользоваться следующими формулами для a и b:

a = y - bx.

Эта формула получена из первого уравнения системы, если все его члены разделены на n: , где cov(x,y) – ковариация признаков; «знаменатель» - дисперсия признака x.

Поскольку , получим следующую формулу расчета оценки параметров b:

Эта формула получается также при решении системы методом определителей, если все элементы расчета разделить на .Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.Знак при коэффициенте регрессии b показывает направление связи: при b > 0 – связь прямая, а при b < 0 – связь обратная.