36. Обработка результатов измерений. Косвенные измерения.

Искомая величина R_x зависит от U и от U₀. R­_x=R₀(U/U₀-1), R₀- const задано .

Для U и U₀ посчитаем значения

1. среднее арифметическое -

2. остаточные погрешности 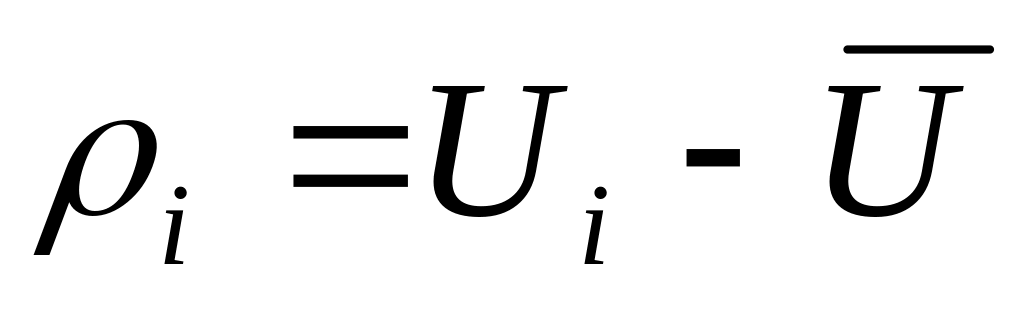, убедиться, что

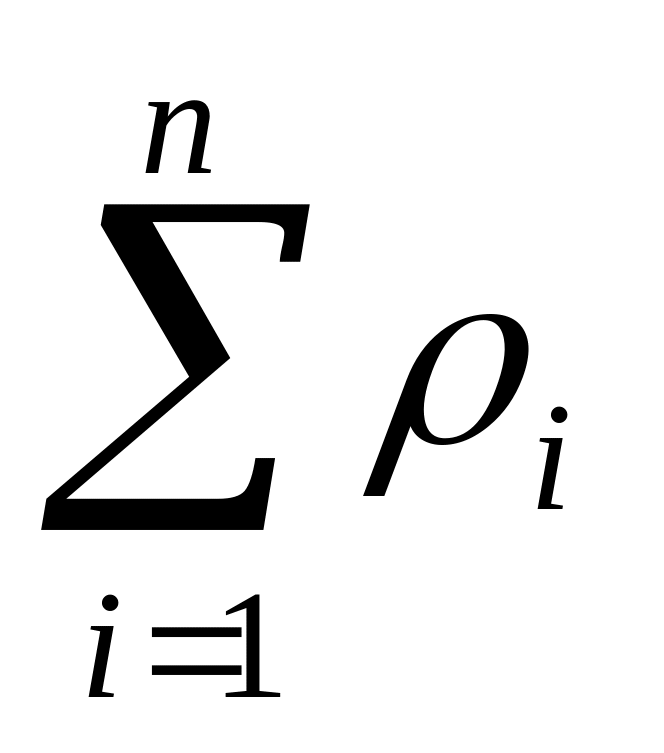
3. найти оценку дисперсии шума

4. найти оценку дисперсии погрешности результата

5. считая что погрешности имеют нормальный закон распределения, найти доверительное значение погрешности измерения 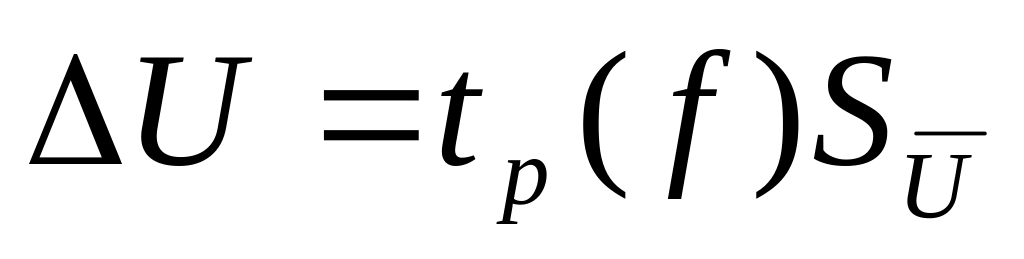, где t_p(f) – коэффициент распределения Стьюдента, соответствующий доверительной вероятности Р и числу степеней свободы. В рассматриваемом случае f=n-1

Зная получим результат измерения

Общее выражение для оценки дисперсии результата измерения R_x имеет вид

, где - оценки дисперсии шума при измерении напряжений U и U₀ соответственно; - оценки дисперсии результатов измерений напряжений U и U₀.

Доверительное значение погрешности результата измерения R_x можно найти по формуле

Окончательный ответ записывается в виде

37. Суммирование составляющих погрешностей распределенных по нормальному закону.

38. Суммирование составляющих погрешностей, закон распределения которых отличен от нормального закона.

Суммарная погрешность складывается из суммы составляющих погрешностей. Для ее оценки можно использовать M, D, СКО

1. МО 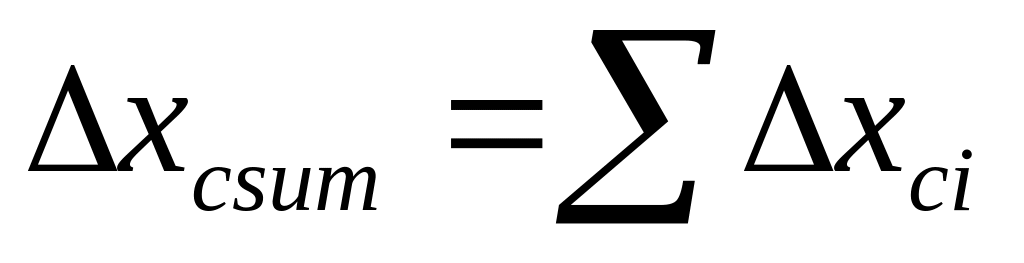- математическое ожидание суммарной погрешности определяется алгебраическим суммированием математических ожиданий составляющих погрешности.

2. . – определяется суммой составляющих дисперсий и необходимо учитывать корреляционные связи.

Делают допущение, 0 если нет и 1 если есть. z_pi берется из таблиц для нормально распределенных с.в. с требуемой вероятностью р_i (*) – арифметическое суммирование погрешностей (**) – геометрическое

Использование арифметического суммирования дает завышенную оценку погрешности, поскольку реальные значения r_ij от 0 до 1.

Если закон распределения отличен от нормального, то в общем виде

Границы доверительного интервала симметричны лишь при Δх_с=0.

Пример:

ΔU_c=0.1В δ=±0,3В

ΔU=-0.2В- 0,4В

Однако знак ΔU_c не известен, а пользоваться не симметричными границами неудобно, ТОО ганица выбираем максимальными ΔU' = -0.4 В – 0.4 В

Так как знак ΔU_с как правило неизвестен, а пользоваться несимметричными границами неудобно, то границы выбирают максимальными. Поскольку выход за границы интервала значений погрешности наблюдается лишь с одной стороны, то вероятность выхода погрешности за границы доверительного интервала уменьшается в 2 раза. (следующее значение вероятности)

±0,3В – p_д=0,9

±0,4В – р_д=0,95

Т.о. в случае Δx_c<>0 можно утверждать следующее