
- •Министерство образования и науки Российской Федерации
- •Содержание
- •1. Исследование равновесия конструкции под действием произвольной плоской системы сил…………………………………………………………………
- •2. Исследование кинематических характеристик механизма, совершающего плоскопараллельное движение.………………………………………………
- •Определение реакций опор составной конструкции (система двух тел).
- •Теоретическая часть.
- •2. Момент силы относительно оси
- •Теорема о плоско - параллельном переносе сил.
- •1.3 Алгоритм решения задачи.
- •2.1 Постановка задачи.
- •2.3 Алгоритм решения задачи.
2. Момент силы относительно оси
Моментом силы относительно оси называется момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.
Момент считается положительным, если с положительного конца оси поворот, который сила стремится совершить, виден происходящим против хода часовой стрелки, и отрицательным – если по ходу часовой стрелки.
![]()

![]() .
.
Чтобы найти момент силы относительно оси, нужно:
1. Провести плоскость перпендикулярную оси z.
2.
Спроецировать силу
![]() на
эту плоскость и вычислить величину
проекции
на
эту плоскость и вычислить величину
проекции
![]() .
.
3. Провести плечо h из точки пересечения оси с плоскостью на линию действия проекции силы и вычислить его длину.
4. Найти произведение этого плеча и проекции силы с соответствующим знаком.
Свойства момента силы относительно оси
Момент силы относительно оси равен нулю, если:
1.
![]() ,
т.е. сила
параллельна
оси.
,
т.е. сила
параллельна
оси.
2. h=0 , т.е. линия действия силы пересекает ось.
Моменты силы относительно координатных осей можно получить, расписав векторное произведение
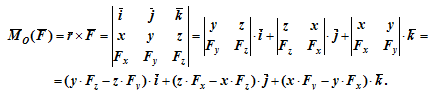
Величины, стоящие в скобках, представляют собой моменты силы F относительно соответствующих осей.
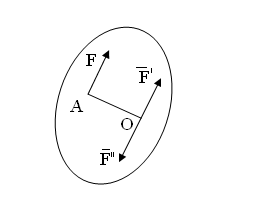
Теорема о плоско - параллельном переносе сил.
Действие силы на твердое тело не изменяется, если эту силу перенести параллельно самой себе в любую другую точку тела добавляя, при этом пару сил, момент которой равен моменту переносимой силы относительно точки, в которую сила переносится.



![]()
![]()

![]()
Процесс замены силы F приложенной в точке А такой же силой приложенной в точке О и пары сил называется приведением силы F к данному центру О.
1.2
Постановка задачи.
Рис. 3.4.
Определение реакций опор составной конструкции.

Дано:
![]() = 9,0 кН;
= 9,0 кН;
![]() =
12,0 кН;
=
12,0 кН;
![]() =
26,0 кН
=
26,0 кН![]() м;
м;
![]() =
4,0 кН/м.
=
4,0 кН/м.
1.3 Алгоритм решения задачи.
1) Определение реакции опоры А при шарнирном соединении в точке С.
Рассмотрим систему уравновешивающихся сил, приложенных ко всей конструкции (рис.2.). Составим уравнение моментов сил относительно точки B.
Рис 2.
![]() (1)
(1)
где
![]() кН.
кН.
После подстановки данных и вычислений уравнение (1) получает вид:
![]() кН (1’)
кН (1’)
Второе
уравнение с неизвестными
![]() и
и
![]() получим, рассмотрев систему
уравновешивающихся сил, приложенных к
части конструкции, расположенной левее
шарнира С
(рис. 3):
получим, рассмотрев систему
уравновешивающихся сил, приложенных к
части конструкции, расположенной левее
шарнира С
(рис. 3):
Рис 3.
![]() .
.
Отсюда
находим, что

 кН.
кН.
Подставив найденное значение в уравнение (1’) найдем значение :
![]() кН.
кН.
Модуль реакции опоры А при шарнирном соединении в точке С равен:
![]() кН.
кН.
2)
Расчетная схема при соединении частей
конструкции в точке С скользящей
заделкой, показанной на 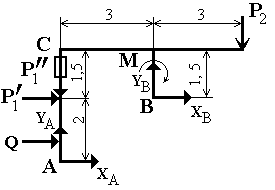
рис. 4.
Системы сил, показанные на рис. 2 и 4, ничем друг от друга не отличаются. Поэтому уравнение (1’) остается в силе. Для получения второго уравнения рассмотрим систему уравновешивающихся сил, приложенных к части конструкции, располоденной левее скользящей заделки С (рис. 5).

рис. 5
Составим уравнение равновесия:
![]()
![]()
откуда
![]()
и из уравнения (1’) находим:
![]()
![]()
Следовательно, модуль реакции при скользящей заделке в шарнире С равен:
![]()
![]() кН.
кН.
Итак, при соединении в точке С скользящей заделкой модуль реакции опоры А меньше, чем при шарнирном соединении (≈ 13%). Найдем составляющие реакции опоры В и скользящей заделки.
Для левой от С части (рис. 5а)
![]() ,
,
откуда
![]() кН.
кН.
Составляющие реакции опоры В и момент в скользящей заделке найдем из уравнений равновесия, составленных для правой от С части конструкции.
![]()
![]()
![]() кН*м
кН*м
![]()
![]() кН
кН
![]()
![]() ;
;
![]() кН
кН
Исследование кинематических характеристик механизма, совершающего плоскопараллельное движение.
Кинематика- раздел теоретической механики, в котором рассматриваются общие геометрические свойства механического движения, как процесса, происходящего в пространстве и во времени. Движущиеся объекты рассматривают как геометрические точки или геометрические тела.
Способы задания движения точки.
Задать движение точки - значит задать изменение ее положения по отношению к выбранной системе отсчета. Существует три основных систем отсчета: векторная, координатная, естественная. Соответственно возможны три способа задания движения точки.
Прежде чем заняться исследованием движения точки, определением характеристик этого движения, надо научиться определять положение точки в пространстве в нужный момент времени.
Векторный способ задания движения точки.
Пусть точка М движется по отношению к некоторой системе отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор , проведенный из начала координат О в точку М.

При
движении точки М
вектор
![]() будет с течением времени изменяться
и по модулю, и по направлению. Следовательно,
является переменным вектором
(вектором-функцией), зависящим от
аргумента
будет с течением времени изменяться
и по модулю, и по направлению. Следовательно,
является переменным вектором
(вектором-функцией), зависящим от
аргумента
![]() :
:
![]()
Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор и найти положение движущейся точки.
Геометрическое место концов вектора , т.е. годограф этого вектора, определяет траекторию движущейся точки.
Координатный способ задания движения точки.
Этим
способом положение точки, в какой либо
системе координат определяется её
координатами
![]() . При движении точки эти координаты
изменяются. Поэтому, чтобы определить
положение точки в нужный момент времени,
должны быть заданы координаты как
функции
. При движении точки эти координаты
изменяются. Поэтому, чтобы определить
положение точки в нужный момент времени,
должны быть заданы координаты как
функции
времени
![]() :
:
![]()
Эти функции называются уравнениями движения точки.
Уравнения движения позволяют определить не только положение точки в любой момент времени, но и все характеристики движения, в том числе и траекторию движения.
Чтобы получить уравнение траектории надо из уравнений движения исключить параметр .
Нетрудно установить зависимость между векторным и координатным способами задания движения.
Разложим вектор на составляющие по осям координат:
![]()
где
![]() -
проекции вектора на оси;
-
проекции вектора на оси;
![]() –
единичные векторы направленные по осям,
орты осей.
–
единичные векторы направленные по осям,
орты осей.
Так как начало вектора находится в начале координат, то проекции вектора будут равны координатам точки M. Поэтому
![]()
Естественный способ задания движения точки

Естественным способом задания движения удобно пользоваться в тех случаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ является траекторией точки М при ее движении относительно системы отсчета Oxyz Выберем на этой траектории какую-нибудь неподвижную точку О', которую примем за начало отсчета, и установим на траектории положительное и отрицательное направления отсчета (как на координатной оси).
Тогда положение точки М на траектории будет однозначно определяться криволинейной координатой s, которая равна расстоянию от точки О' до точки М, измеренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка М перемещается в положения M1, М2,... . следовательно, расстояние s будет с течением времени изменяться.
Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость
![]() .
.
Уравнение выражает закон движения точки М вдоль траектории.
Скорость и ускорение точки при естественном способе задания движения.
Из определения скорости точки

где
![]()
- единичный вектор касательной, тогда
![]()
Алгебраическая скорость – это проекция вектора скорости на касательную, равная производной от дуговой координаты по времени. Если производная положительна, то точка движется в положительном направлении отсчета дуговой координаты.
Из определения ускорения

поскольку τ - переменный по направлению вектор, то:

Производная
![]()
определяется только свойствами траектории в окрестности данной точки, при этом

n - единичный вектор главной нормали,
ρ - радиус кривизны траектории в данной точке.
Таким образом,

т.е. вектор ускорения раскладывается на две составляющие - касательное и нормальное ускорения:
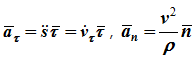
Здесь:

- алгебраическое значение касательного ускорения (проекция вектора ускорения на касательную) характеризует изменение скорости по величине;

– нормальное ускорение (проекция вектора ускорения на главную нормаль) характеризует изменение скорости по направлению. Вектор ускорения всегда лежит в соприкасающейся плоскости и проекция ускорения на бинормаль равна нулю (ab=0).
Поступательное движение тела.
Поступательным называют движение, при котором прямая, проведенная через две точки тела, остается параллельной ее первоначальному положению .
Доказана теорема: при поступательном движении все точки тела движутся по одинаковым траекториям и имеют в каждой момент времени одинаковые по модулю и направлению скорости и ускорения.
Вывод: Поступательное движение твердого тела определяется движением любой его точки, в связи с чем, задание и изучение его движения сводится к кинематике точки.
Вращательные движения тела вокруг неподвижной оси.
Вращательным движением вокруг неподвижной оси называют движение твердого тела, при котором две точки, принадлежащие телу, остаются неподвижными в течение всего времени движения. Указанная прямая называется осью вращения, при таком движении траектории движения точек такого тела есть окружность в центре по оси.
Угол,
отсчитываемый от неподвижной полуплоскости
против движения часовой стрелки,
измеряемый в радианах, называется углом
поворота тела -
![]() .
Уравнение вращения тела вокруг неподвижной
оси выражает зависимость угла поворота
от времени:
.
Уравнение вращения тела вокруг неподвижной
оси выражает зависимость угла поворота
от времени:
![]()

Основными
характеристиками вращательного движения
тела являются угловая скорость -
![]() и
угловое ускорение -
и
угловое ускорение -
![]() .
.
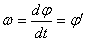
Размерность
[
]
= [рад/с] =[
![]() ]
.
]
.
Величина,
характеризующая быстроту изменения
угла поворота с течением времени,
называется угловой скоростью тела -
Угловую скорость тела можно изобразить
в виде вектора
![]() ,
численная величина которого равна
,
численная величина которого равна
![]() и
который направлен вдоль оси вращения
тела в ту сторону, откуда вращение видно
происходящим против хода часовой
стрелки.
и
который направлен вдоль оси вращения
тела в ту сторону, откуда вращение видно
происходящим против хода часовой
стрелки.
Такой
вектор сразу определяет и модуль угловой
скорости, и ось вращения, и направление
вращения вокруг этой оси.
В технике
угловую скорость часто выражают не в
радианах в секунду, а частотой вращения
n, выраженной числом оборотов в минуту.
Зависимость между n и
с
учетом того, что каждый оборот содержит
![]() рад,
имеет вид
рад,
имеет вид
![]()
Угловое
ускорение тела (по аналогии с угловой
скоростью) можно также изобразить в
виде вектора
![]() ,
направленного вдоль оси вращения. При
этом направление
совпадает
с направлением
,
направленного вдоль оси вращения. При
этом направление
совпадает
с направлением
![]() ,
когда тело вращается ускоренно и
противоположно
при
замедленном вращении (рис. а, б).
,
когда тело вращается ускоренно и
противоположно
при
замедленном вращении (рис. а, б).

 [рад/
[рад/![]() ]
]
Величины
![]() n
являются угловыми характеристиками,
применимы-ми для всего тела в целом. Их
нельзя относить к отдельной точке
вращающегося тела или к другой какой-либо
точке. Движение точки характеризуется
линейными величинами: скоростью
n
являются угловыми характеристиками,
применимы-ми для всего тела в целом. Их
нельзя относить к отдельной точке
вращающегося тела или к другой какой-либо
точке. Движение точки характеризуется
линейными величинами: скоростью
![]() и
ускорением
и
ускорением
![]() .
.

или
![]()
При равнопеременном вращении постоянно угловое ускорение:
![]()
![]()
При
![]() и
и
![]() получим
получим
![]()
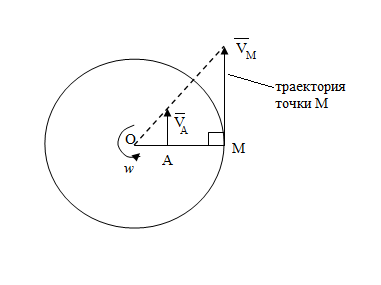
Скорости и ускорения точек тела при вращательном движении.
Пусть М – произвольная точка тела.
ОМ=R – расстояние от этой точки до оси вращения.
![]() - скорость точки.
- скорость точки.
![]()
перпендикулярен
ОМ и направлен в соответствии
с
![]() .
.
перпендикулярен .
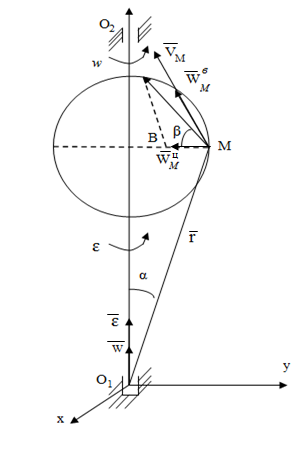
r – радиус вектора точки М.
![]()
![]() .
.
перпендикулярно
![]() и
и
![]() перпендикулярно
перпендикулярно
![]() .
.
![]()
![]() ;
;
![]() перпендикулярно
перпендикулярно![]() .
.
вектор вращательного ускорения точки при ускоренном вращении тела он направлен также как и вектор скорости; при замедленном вращении противоположен вектору скорости.
![]() - величина
вращательного ускорения.
- величина
вращательного ускорения.
- вектор центростремительного ускорения точки, всегда направлен от точки М к оси вращения.
![]() - величина
центростремительного ускорения.
- величина
центростремительного ускорения.
Полное ускорение.
![]()
![]()
Таким образом, ускорение точек тела при вращательном ускорении, так же как и их скорости пропорциональны расстоянию от этих точек до оси вращения.
 - этот угол не
зависит от положения точек.
- этот угол не
зависит от положения точек.

