
- •Лекция № 13
- •Магнетизм
- •Магнитное поле
- •13.1 Магнитное поле в вакууме
- •1) Взаимодействие токов
- •2) Магнитное поле и его свойства
- •13.2. Рамка с током
- •Рамка с током в магнитном поле
- •13.4. Макротоки и микротоки
- •13.6. Подобие векторных характеристик электростатического
- •13.7. Закон Био-Савара-Лапласа (Основной закон магнитного поля тока)
- •13.8. Магнитное поле прямого тока
- •13.9. Магнитное поле в центре кругового тока (витка с током)
- •13.10. Закон Ампера
- •13.11. Взаимодействие параллельных токов
13.6. Подобие векторных характеристик электростатического
и магнитного полей
Вектор магнитной индукции В — аналог вектора напряженности электростатического поля Е. Эти величины определяют силовые действия этих полей и зависят от свойств среды.
Аналогом вектора электрического смещения D является вектор напряженности Н магнитного поля.
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций полей, создаваемых каждым током или движущимся зарядом.
13.7. Закон Био-Савара-Лапласа (Основной закон магнитного поля тока)
(магнитное поле кривого тока)
Э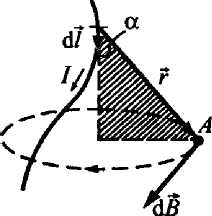 лемент
проводника
лемент
проводника
![]() с током
создает
в некоторой точке А
магнитную индукцию
поля:
с током
создает
в некоторой точке А
магнитную индукцию
поля:
![]()
,
![]()
где
![]() — радиус-вектор,
проведенный из элемента dl
проводника в точку
А.
— радиус-вектор,
проведенный из элемента dl
проводника в точку
А.
Н![]() аправление
аправление
![]() перпендикулярно
и
,
и совпадает с касательной к линии
магнитной индукции.
перпендикулярно
и
,
и совпадает с касательной к линии
магнитной индукции.
Модуль вектора определяется выражением: (1)
где — угол между векторами и .
13.8. Магнитное поле прямого тока
а) для проводника бесконечной
длины
(α
измен. от 0 до π
)







dl
α
r∙dα![]()
r
Из рисунка


l
![]() -
элемент
тока
-
элемент
тока
dα![]()


α

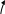

R
A




I
![]()
![]() Ток
течет по прямому проводу бесконечной
длины. В качестве постоянной интегрирования
выберем угол
.
Из рисунка
Ток
течет по прямому проводу бесконечной
длины. В качестве постоянной интегрирования
выберем угол
.
Из рисунка
![]() ,
,
![]() .
Подставив в формулу (1), получим:
.
Подставив в формулу (1), получим:
Угол α для всех элементов прямого провода изменяется от 0 до π. По принципу суперпозиции:
![]()
Итак, прямой провод бесконечной длины создает вектор магнитной индукции
![]()
б )
для отрезка проводника
)
для отрезка проводника
Если ток течет по отрезку провода (см. рисунок) , то вектор магнитной индукции, создаваемый им в точке А:
![]()
(1)
Эта формула переходит в формулу для бесконечного проводника при α1 = 0, α2 = π. Иногда на практике бывает удобнее пользоваться формулой
![]()
(2) , где
![]() и
и
![]() - углы, под которыми
видны концы проводника
из точки А, в которой измеряется магнитная
индукция. Тогда
- углы, под которыми
видны концы проводника
из точки А, в которой измеряется магнитная
индукция. Тогда
![]() ,
а
,
а
![]()
![]() ;
;
![]() .
.
Очевидно, что:
![]() .
Подставив это в (1), получаем (2).
.
Подставив это в (1), получаем (2).
13.9. Магнитное поле в центре кругового тока (витка с током)
В данном случае сложение векторов можно
заменить сложением их модулей, учитывая
sinα = 1 , r =
R:
данном случае сложение векторов можно
заменить сложением их модулей, учитывая
sinα = 1 , r =
R:
pm![]()
![]() Можно
показать, что на расстоянии r
от центра витка вдоль оси витка магнитное
поле будет:
Можно
показать, что на расстоянии r
от центра витка вдоль оси витка магнитное
поле будет:
![]()
Напряженность магнитного поля, создаваемого круговым током, на большом расстоянии от витка с током (r >> R):
![]()
Где: pm = IS – магнитный момент витка с током.
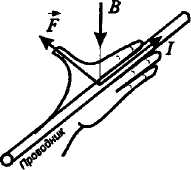
13.10. Закон Ампера
Действие магнитного поля на рамку с током – это пример воздействия магнитного поля на проводник с током.
Ампер установил, что сила
![]() , с которой магнитное поле действует на
элемент проводника
, с которой магнитное поле действует на
элемент проводника
![]() с
током I, находящегося в
магнитном поле, равна:
с
током I, находящегося в
магнитном поле, равна:
![]()
или в
скалярной форме
![]() , где :
, где :
— вектор по модулю равный dl и совпадающий
по направлению с током,
— вектор магнитной индукции,
α — угол между направлением тока и вектором .
Наглядно направление силы Ампера принято определять по правилу левой руки.
Правило левой руки:
Е сли
ладонь левой руки расположить так, чтобы
в нее входил
сли
ладонь левой руки расположить так, чтобы
в нее входил
вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы Ампера.
