2.4.4 Прямолинейное движение робота с одной точкой опоры по шероховатой поверхности

При прямолинейном движении робота с одной точкой опоры (N_A>0, N_B=0) сила трения в этой точке равна предельной ( ), , .

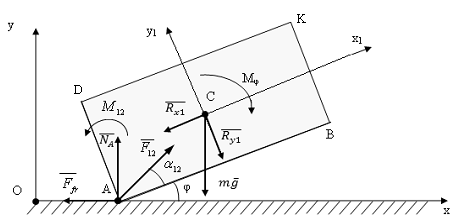
Рис. 6.4 Расчетная схема робота при прямолинейном движении робота с одной точкой опоры

Система уравнений в этом режиме записывается в виде:

(4)

и требует решения относительно нормальной реакции в точке А и перемещения центра масс корпуса вдоль оси Ох.

Нормальная реакция в точке А равна

.

Линейное ускорение центра масс корпуса рассчитывается по формуле:

Последнее уравнение в системе определяет условие, при котором наблюдается данный режим движения робота:

.

2.4.5 Поворот относительно точки а

Рассмотрим случай, когда нормальная реакция в точке А положительна (N_A>0, ), нормальная реакция в точке В равна 0 (N_B=0) и сила трения в точке А не превышает предельную ( ), т.е. система совершает поворот вокруг точки А.

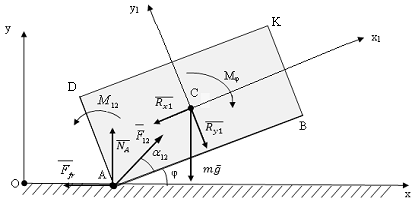
Рис. 6.5 Расчетная схема робота при вращательном движении относительно точки А

Уравнения связи имеют вид:

,

Система уравнений при вращательном движении корпуса относительно точки А имеет вид:

(5)

где J_A=2m(a²+b²) – момент инерции корпуса робота относительно точки А.

Неизвестными являются нормальная реакция N_A и сила трения F_fr в точке А и поворот φ корпуса относительно его центра масс, которые находятся по формулам:

,

, .

2.4.6 Плоскопараллельное движение без отрыва от поверхности

При плоскопараллельном движении без отрыва корпуса от поверхности робот имеет одну точку опоры А (N_A>0, N_B=0), сила трения в которой равна предельной ( ).

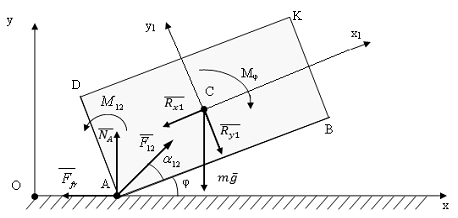
Рис. 6.6 Расчетная схема робота при плоскопараллельном движении

Уравнение связи записывается в виде:

Система уравнений, описывающих плоскопараллельное движение робота без отрыва от поверхности

(6)

где J_C=m(a²+b²), требует решения относительно неизвестных нормальной реакции в точке А и двух обобщенных координат – перемещения центра масс корпуса вдоль оси Ох и угла поворота корпуса.

Нормальная реакция в точке А равна

.

Линейное и угловое ускорения центра масс корпуса рассчитываются по формулам:

2.4.7 Плоскопараллельное движение при отрыве от поверхности

После того, как произошел отрыв обеих точек опоры корпуса от поверхности (N_A = 0, N_B = 0), но ордината точки А по оси Оу не достигла некоторого значения y^*=lsin(α₁₂+φ) ( ), наблюдается плоскопараллельное движение корпуса робота под действием силы F₁₂=F₁₂(t) и момента M₁₂=M₁₂(t).

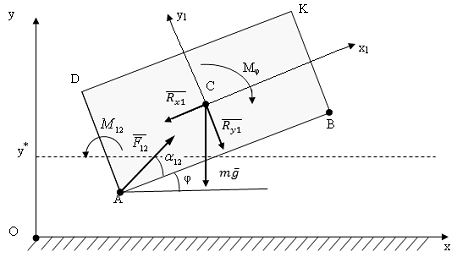
Рис. 6.7 Расчетная схема при плоскопараллельном движении с отрывом от поверхности

Получим систему уравнений, описывающих состояние системы,

(7)

из которой определим неизвестные обобщенные координаты:

2.5 Алгоритм моделирования одного прыжка робота

Представленный на рис. 6.1 алгоритм позволяет исследовать линейные и угловые характеристики прыгающего робота.

Моделирование движения робота проводится при нулевых начальных условиях: t=0, x_C=0, , y_C=0, 0, , =0, . Формирование матрицы результатов моделирования осуществляется пошагово при помощи счетчика i, шаг по времени равен t. Циклический пересчет характеристик робота по времени обеспечивает выполнение условия t_i<T_k, где t_i – время на i-ом шаге, T_k – конечное время. Параметры исследуемой системы: масса корпуса m=5 кг, геометрические размеры а=0,25 м, b=0,15 м, моменты инерции корпуса относительно точек С и А J_C=0,85 кг·м², J₁=1,7 кг·м², коэффициент трения скольжения f=0,2, момент и сила, создаваемые приводами М₁₂=30 Нм, F₁₂=500 Н. Движение робота происходит в среде с нулевыми коэффициентами вязкости: μ_x1= μ_y1=μ_φ=0 Н·с/м.

Моделирование движения робота проводится по алгоритму, приведенному на рис. 7. Определение фазы прыжка, в которой находится объект, осуществляется при помощи счетчика n. Значение n=0 соответствует фазе разгона, которая заканчивается в момент обнуления нормальной реакции в стопе робота , счетчик становится равным n=1. В результате этого робот переходит в фазу полета, в которой находится до тех пор, пока не обнулится ордината одной из опорных точек корпуса робота. При выполнении указанного условия счетчик принимает новое значение n=2, объект переходит в фазу приземления, которая заканчивается после того, как вторая точка корпуса станет взаимодействовать с поверхностью. При этом счетчик становится равным n=3, после чего цикл прыжка завершается.

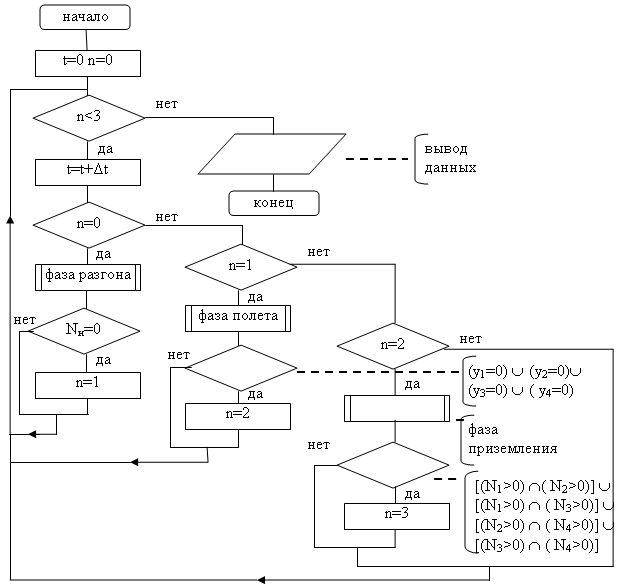
Рис. 7. Алгоритм моделирования одного прыжка робота вместо n писать другую букву и в пояснении алгоритма тоже

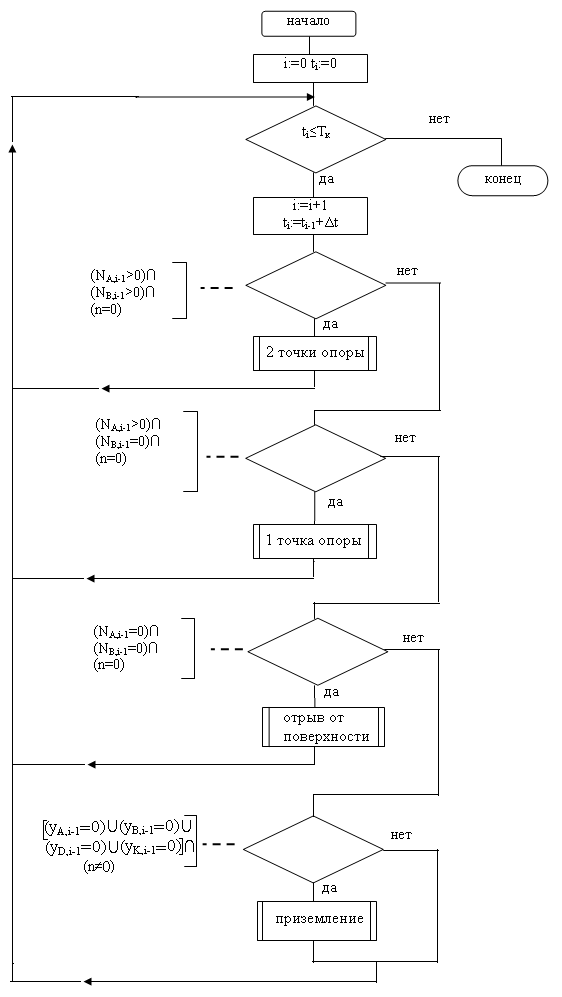
Рис. 6.1 Алгоритм моделирования одного прыжка робота переделать под фазу разгона

В фазе разгона по значениям нормальных реакций определяется число точек корпуса робота, взаимодействующих с поверхностью.

При двух положительных нормальных реакциях (рис. 6.2) робот в соответствии с используемой моделью сухого трения может находиться в трех режимах: статика с двумя точками опоры, если абсцисса скорости центра масс равна нулю и сила трения в опоре А меньше предельной, прямолинейное движение вдоль оси Ох, при ненулевой горизонтальной составляющей скорости центра масс, переход из статического положения на двух опорах к прямолинейному, когда горизонтальная составляющая скорости центра масс равна нулю и сила трения достигла предельного значения.

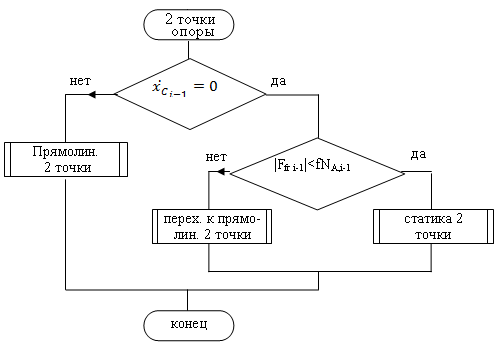
Рис. 6.2 Алгоритм процедуры движения робота с двумя точками опоры в фазе разгона

Если корпус робота взаимодействует с поверхностью в одной точке – т. А ( ), то робот может находиться в следующих режимах (рис. 6.3). При равенстве нулю горизонтальной составляющей скорости точки А и силе трения меньше предельной робот либо вращается относительно неподвижной точки А, либо находится в состоянии покоя при одной точке опоры (когда ), если же сила трения равна предельной, то наблюдается переход из вращательного движения в плоскопараллельное без отрыва от поверхности. Последнее будет реализовано при ненулевой горизонтальной проекции скорости точки А, также возможен режим прямолинейного движения с одной точкой опоры при нулевой угловой скорости.

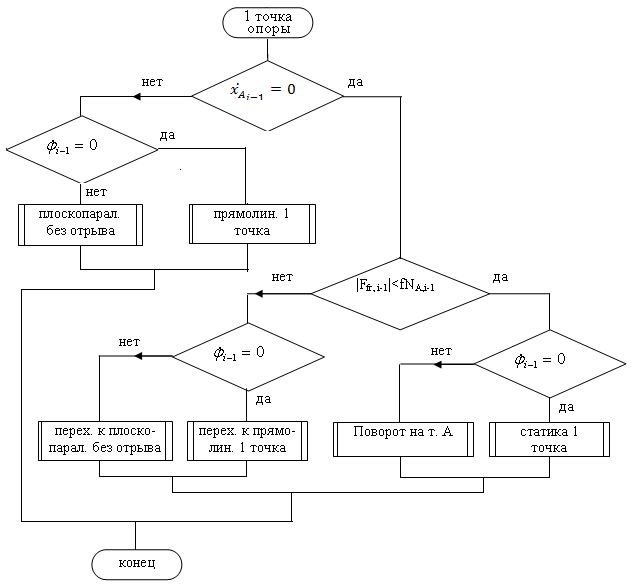
Рис. 6.3 Алгоритм процедуры движения робота с одной точкой опоры в фазе разгона

После отрыва обеих точек А и В от поверхности в зависимости от ординаты точки А робот может находиться в фазе разгона под действием силы F₁₂ ( ) или же совершать полет под действием сил инерции и тяжести при невыполнении указанного условия (рис. 6.4).

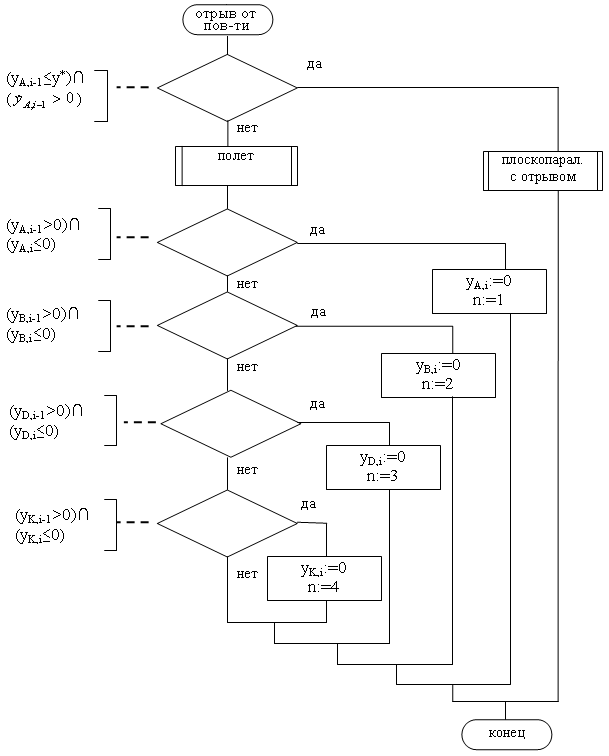
Рис. 5.4 Алгоритм процедуры движения робота при отрыве от поверхности

Как только ордината одной из точек корпуса обнулится, начинается режим приземления, в котором корпус поворачивается относительно неподвижной точки приземления до тех пор, пока вторая точка не окажется на поверхности и робот не перейдет в статическое положение с двумя точками опоры (рис. 6.5). На рис. 6.6 рассмотрен алгоритм приземления робота на точку А.

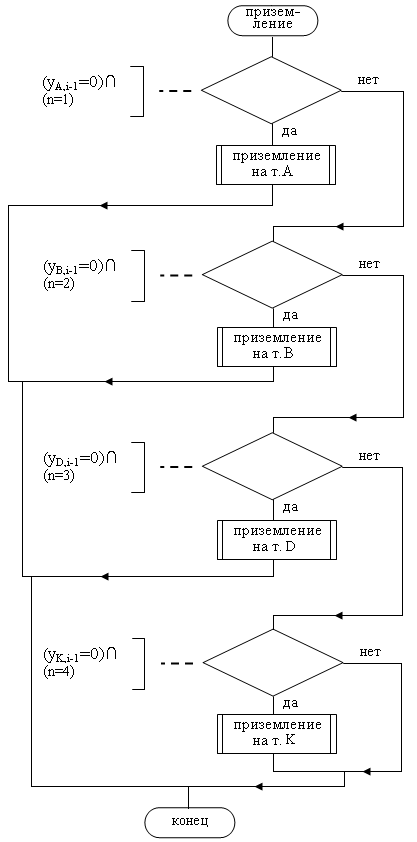
Рис. 6.5 Алгоритм процедуры приземления робота

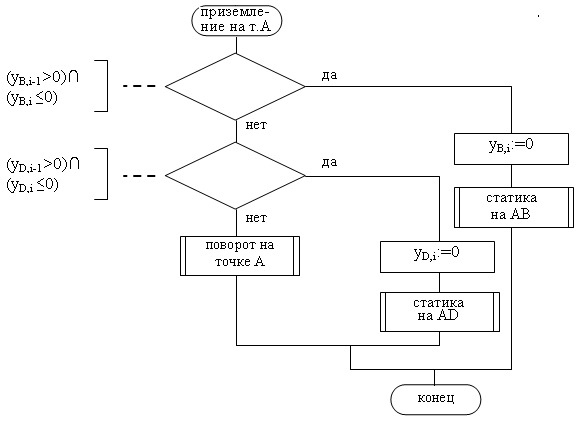
Рис. 6.6 Алгоритм процедуры приземления робота на точку А