
- •Предмет молекулярной физики. Основные положения молекулярно- кинетической теории. Идеальный газ.
- •2.Законы идеального газа. Уравнение состояния идеального газа (уравнение Менделеева - Клапейрона). Физический смысл универсальной газовой постоянной.
- •4.Степени свободы молекул идеального газа. Теорема Больцмана о распределении энергии по степеням свободы молекул идеального газа.
- •5.Распределение молекул идеального газа по скоростям (распределение Максвелла). Графическое представление и анализ функции распределения.
- •6. Скорости молекул идеального газа (наиболее вероятная, среднеарифметическая, среднеквадратичная)
- •7. Опыт Штерна
- •8. Идеальный газ во внешнем силовом поле. Барометрическая формула.
- •9.Распределение Больцмана.
- •10.Предмет термодинамики. Термодинамическая сила.
- •11. Равновесные и неравновесные состояния.
- •12. Равновесный процесс.Работа при изменении состояния идеального газа.
- •16.Теплоемкость идеального газа при постоянном объеме.
- •17. Теплоемкость газа при постоянном давлении
- •18. Первый закон термодинамики применительно к изопроцессам. Работа идеального газа в этих условиях.
- •19. Адиабатический процесс
- •2 0.Первый закон термодинамики применительно к адиабатическому процессу . Работа идеального газа при адиабатическом процессе.
- •21.Круговые процессы(циклы) кпд кругового процесса.
- •22.Обратимые и необратимые процессы.
Предмет молекулярной физики. Основные положения молекулярно- кинетической теории. Идеальный газ.
Молекулярная физика – статистическая теория.
Молекулярная физика – раздел, в котором изучаются макроскопические свойства вещества, обусловленные его молекулярным строением, характером движения молекул и силами, действующими между ними.
Термодинамика – фенологическая наука, которая делает вывод о свойствах вещества на основе законов, установленных на опыте.
Молекулярно – кинетическая теория – учение о строении и свойствах вещества на основе представлении о существовании атомов и молекул как наименьших частиц химических веществ.
3 закона.
Все вещества составляются из мельчайших частиц
Атомы и молекулы находятся в непрерывном хаотическом движении
Электрическая природа
Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.По эквивалентной формулировке идеальный газ - такой газ, который одновременно подчиняется закону Бойля — Мариотта и Гей-Люссака, то есть:
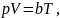 Pa6cv/T
= R = сonst (2.27)
где v — удельный объем газа; R —
универсальная газовая постоянная.
Pa6cv/T
= R = сonst (2.27)
где v — удельный объем газа; R —
универсальная газовая постоянная.
Где P — давление T — абсолютная температура. Свойства идеального газа описываются уравнением Менделеева — Клапейрона
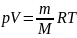 ,
где R-
универсальная газовая постоянная, m —
масса, M —
молярная масса. Или p=nkT,
где n —
концентрация частиц, k —
постоянная Больцмана.
,
где R-
универсальная газовая постоянная, m —
масса, M —
молярная масса. Или p=nkT,
где n —
концентрация частиц, k —
постоянная Больцмана.
Для любого идеального газа справедливо соотношение Майера
 Где
R—
универсальная газовая постоянная,
Где
R—
универсальная газовая постоянная,
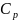 —
молярная теплоемкость при постоянном
давлении,
—
молярная теплоемкость при постоянном
давлении,
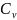 —
молярная теплоемкость при постоянном
объёме.
—
молярная теплоемкость при постоянном
объёме.
2.Законы идеального газа. Уравнение состояния идеального газа (уравнение Менделеева - Клапейрона). Физический смысл универсальной газовой постоянной.
а) Закон Бойля - Mаpuomma: при неизменных температуре и массе произведение численных значений давления и объема газа постоянно: pV = const P1v1 = P2v2 = const
Закон Гей-Люссака: при постоянном давлении объем данной массы газа прямо пропорционален его абсолютной температуре: V = V0(1 + at) где V - объем газа при температуре t, °С; V0 – его объем при 0°С. Величина a называется температурным коэффициентом объемного расширения. Для всех газов a = (1/273°С–1). Следовательно, V = V0(1 +(1/273)t)
Закон Шарля: при постоянном объеме давление данной массы газа прямо пропорционально его абсолютной температуре: p = p0(1+gt) где р0 - давление газа при температуре t = 273,15 К. Величина g называется температурным коэффициентом давления. Ее значение не зависит от природы газа; для всех газов = 1/273 °С–1. Таким образом, p = p0(1 +(1/273)t)
Закон Авогадро: различные газы, занимающие одинаковые объемы при равных условиях (одинаковых давлении и температуре), содержат одинаковое число молекул. Это число для 1 грамм-молекулы (1 моль) любого газа составляет около 6,025•1023 и называется числом Авогадро. Таким образом, массы различных газов, занимающие одинаковый объем при равных условиях, соотносятся между собой как их молекулярные массы. Средний объем 1 моль двухатомных газов и метана равен 22,4 л, соответственно, объем 1 кмоль сжиженных газов приблизительно равен 22 м3.
Уравнение состояния идеального газа: PV = nRT , где n – число молей газа;P – давление газа (например, в атм;V – объем газа (в литрах);T – температура газа (в кельвинах);R – газовая постоянная (0,0821 л·атм/моль·K).
Если (Т2-Т1)=1К, то для 1 моля газа R=A, т.е. R численно равна работе изобарного расширения 1 моля идеального газа при нагревании его на 1 кельвин.
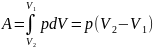
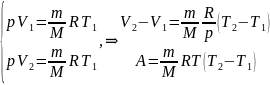
3.
Основное уравнение молекулярно –
кинетической теории идеального газа.
Средний квадрат скорости молекул
идеального газа.
![]() ,
где k
является постоянной Больцмана (отношение
универсальной газовой постоянной R
к числу Авогадро NA),
i
— число степеней свободы молекул (
,
где k
является постоянной Больцмана (отношение
универсальной газовой постоянной R
к числу Авогадро NA),
i
— число степеней свободы молекул (![]() в большинстве задач про идеальные газы,
где молекулы предполагаются сферами
малого радиуса, физическим аналогом
которых могут служить инертные газы),
а T
- абсолютная температура.
в большинстве задач про идеальные газы,
где молекулы предполагаются сферами
малого радиуса, физическим аналогом
которых могут служить инертные газы),
а T
- абсолютная температура.
Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) газовой системы с микроскопическими (масса молекул, средняя скорость их движения).
Уравнение
среднеквадратичной скорости молекулы
легко выводится из основного уравнения
МКТ для одного моля газа.
![]() ,
для 1 моля
,
для 1 моля
![]() ,
где
,
где
![]() —
постоянная Авогадро
—
постоянная Авогадро
![]() ,
где
,
где
![]() —
молярная масса газа
Отсюда
окончательно
—
молярная масса газа
Отсюда
окончательно![]()
