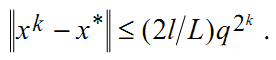- •Элементы выпуклого анализа.
- •Начальные сведения о численных методах оптимизации.
- •4.Сходимость методов оптимизации.
- •5.Метод покоординатного спуска.
- •6.Метод случайного поиска. Алгоритм с возвратом при неудачном шаге.
- •7. Метод случайного поиска. Алгоритм наилучшей пробы.
- •8. Метод случайного поиска. Алгоритм статистического градиента.
- •9. Метод случайного поиска. Алгоритм покоординатного обучения.
- •10. Градиентный метод. Метод с постоянным шагом.
- •11. Градиентный метод. Метод с дроблением шага.
- •12. Градиентный метод. Метод наискорейшего спуска.
- •13. Метод Ньютона
- •14. Численные методы решения задач линейного программирования. Прямой симплекс-метод. Базис и базисное решение.
- •15. Численные методы решения задач линейного программирования. Прямой симплекс-метод. Элементарные преобразования. Симплекс-таблицы.
- •16. Численные методы решения задач линейного программирования. Прямой симплекс-метод. Алгоритм симплекс-метода.
- •17. Численные методы решения задач линейного программирования. Модифицированный симплекс-метод.
- •18. Численные методы решения задач линейного программирования. Лексикографический прямой симплекс-метод
- •19. Численные методы решения задач линейного программирования. Двойственный симплекс-метод.
- •20. Численные методы решения задач линейного программирования. Двойственный симплекс-метод.
- •22. Численные методы решения задач линейного программирования. Геометрическая интерпретация задач линейного программирования
- •23. Численные методы решения задач линейного программирования. Геометрическая интерпретация прямого симплекс-метода.
- •24. Численные методы условной оптимизации. Метод возможных направлений.
- •25. Численные методы условной оптимизации. Метод Келли и метод секущих плоскостей.
- •26. Численные методы условной оптимизации. Первый (циклический) алгоритм Гомори.
- •27. Численные методы условной оптимизации. Метод ветвей и границ
- •28. Численные методы условной оптимизации. Метод ветвей и границ для решения задач нелинейного программирования
- •29. Численные методы условной оптимизации. Метод внешних штрафов
- •30.Численные методы условной оптимизации. Метод внутренних штрафов или метод барьерных функций
- •31.Муравьиный алгоритм.
- •32.Генетические алгоритмы.
- •33.Задачи классического вариационного исчисления. Постановка задачи классического вариационного исчисления
- •Сильный и слабый экстремум в задачах классического вариационного исчисления.
- •Допустимые управления и управляемые процессы в задачах оптимального управления. Оптимальные процессы
- •Элементарный вывод необходимых условий экстремума для простейших задач классического вариационного исчисления
- •Задачи оптимального управления. Постановка задачи оптимального управления
- •Формулировка принципа максимума для линейной задачи быстродействия
- •Доказательство принципа максимума для линейной задачи быстродействия.
- •Достаточность принципа максимума
11. Градиентный метод. Метод с дроблением шага.
В
этом варианте градиентного метода
величина шага
на каждой итерации выбирается из условия
выполнения неравенства
![]() (2)
(2)
где
-
![]() некоторая заранее выбранная константа.
некоторая заранее выбранная константа.
Процедуру
нахождения такого
обычно оформляют так. Выбирается число
![]() и некоторый начальный шаг
и некоторый начальный шаг
![]() .
Теперь для каждого k
полагают
.
Теперь для каждого k
полагают
![]() и делают шаг градиентного метода. Если
с таким
условие (2) выполняется, то переходят к
следующему k.
Если же (2) не выполняется, то умножают
на
и делают шаг градиентного метода. Если
с таким
условие (2) выполняется, то переходят к
следующему k.
Если же (2) не выполняется, то умножают
на
![]() ("дробят шаг") и повторяют эту
процедуру до тех пор пока неравенство
(2) не будет выполняться. В условиях
теоремы 1 эта процедура для каждого k
за конечное число шагов приводит к
нужному
.
("дробят шаг") и повторяют эту
процедуру до тех пор пока неравенство
(2) не будет выполняться. В условиях
теоремы 1 эта процедура для каждого k
за конечное число шагов приводит к
нужному
.
Можно
показать, что в условиях теоремы 2
градиентный метод с дроблением шага
линейно сходится. Описанный алгоритм
избавляет нас от проблемы выбора
на каждом шаге, заменяя ее на проблему
выбора параметров
![]() и
,
к которым градиентный метод менее
чувствителен. При этом, разумеется,
объем вычислений возрастает (в связи с
необходимостью процедуры дробления
шага), впрочем, не очень сильно, поскольку
в большинстве задач основные вычислительные
затраты ложатся на вычисление градиента.
и
,
к которым градиентный метод менее
чувствителен. При этом, разумеется,
объем вычислений возрастает (в связи с
необходимостью процедуры дробления
шага), впрочем, не очень сильно, поскольку
в большинстве задач основные вычислительные
затраты ложатся на вычисление градиента.
12. Градиентный метод. Метод наискорейшего спуска.
Этот
вариант градиентного метода основывается
на выборе шага из следующего соображения.
Из точки x[k]
будем двигаться в направлении
антиградиента до тех пор пока не достигнем
минимума функции f на этом направлении,
т. е. на луче
![]() :
:
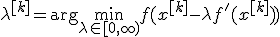
Другими словами, выбирается так, чтобы следующая итерация была точкой минимума функции f на луче L (см. рис. 3). Такой вариант градиентного метода называется методом наискорейшего спуска. Заметим, кстати, что в этом методе направления соседних шагов ортогональны.
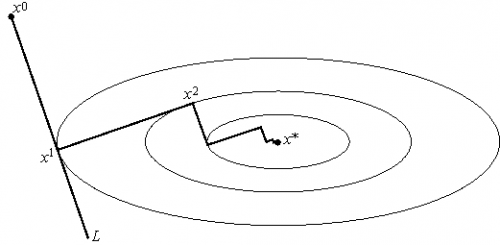
Рис.3 Геометрическая интерпретация метода наискорейшего спуска. На каждом шаге выбирается так, чтобы следующая итерация была точкой минимума функции f на луче L.
Метод наискорейшего спуска требует решения на каждом шаге задачи одномерной оптимизации. Практика показывает, что этот метод часто требует меньшего числа операций, чем градиентный метод с постоянным шагом.
В общей ситуации, тем не менее, теоретическая скорость сходимости метода наискорейшего спуска не выше скорости сходимости градиентного метода с постоянным (оптимальным) шагом.
13. Метод Ньютона
Перейдем к изложению метода второго порядка, использующего вторые частные производные минимизируемой функции f(x) . Рассматриваемый далее метод является прямым обобщением метода Ньютона для отыскания решения системы уравнений ɸ(x)=0, где ɸ:Rn→Rn . Возьмем линейную аппроксимацию функции ɸ(x) в окрестности точки xk и перепишем векторное уравнение в следующем виде:
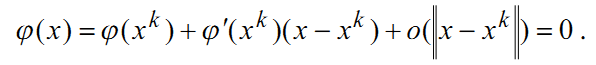
Отбрасывая последний член в этом разложении, получим линейную систему уравнений относительно нового приближения xk+1 . Таким образом, метод Ньютона для отыскания решения системы уравнений описывается следующей формулой:
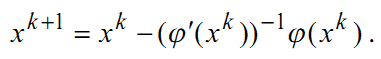
Пусть функция ɸ(x) является градиентом некоторой функции f(x) . Формула метода Ньютона для решения уравнения f’(x)=0 выглядит так:
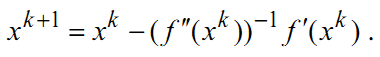
В этом случае метод Ньютона можно интерпретировать как поиск точки минимума квадратичной аппроксимации функции f(x) в окрестности точки xk.
Пусть последовательность {xk}kεN получена с помощью метода Ньютона и точка x* – глобальный минимум функции f . Следующая теорема дает условия квадратичной скорости сходимости метода.
Теорема 4. Пусть дважды непрерывно дифференцируемая функция f сильно выпукла с константой l > 0 , вторая производная удовлетворяет условию Липшица
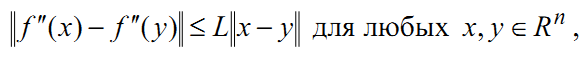
и
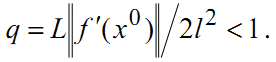 Тогда xk→x*
при k→∞,
и метод Ньютона имеет квадратичную
скорость сходимости
Тогда xk→x*
при k→∞,
и метод Ньютона имеет квадратичную
скорость сходимости