4.Сходимость методов оптимизации.
Важной характеристикой бесконечношаговых методов является сходимость. Будем говорить, что метод, задаваемый соотношением xk+1=xk+akhk, ak ϵ R,k=0,1,2… сходится,
если xk → x* при k→∞ , где x* – решение задачи:
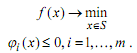
Если f(xk)→f(x*) при k→∞, то иногда также говорят о сходимости по функции, при этом последовательность {xk}kϵN называют минимизирующей. Минимизирующая последовательность может и не сходиться к точке минимума. В случае, когда точка минимума x* не единственна, под сходимостью метода понимается сходимость {xk}kϵN к множеству Q* точек минимума функции f .
Эффективность сходящегося метода можно охарактеризовать с помощью понятия скорости сходимости. Пусть xk → x* при k→∞. Говорят, что последовательность {xk}kϵN сходится к x* линейно (с линейной скоростью, со скоростью геометрической прогрессии), если существуют такие константы qϵ(0,1) и k0 , что
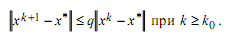(9)
Говорят, что {xk}kϵN сходится к x* сверхлинейно (со сверхлинейной скоростью), если
Говорят о квадратичной сходимости, если существуют такие константы С ≥ 0 и k0, что
Иногда, сохраняя ту же терминологию, неравенства (9)-(11) заменяют соответственно на неравенства
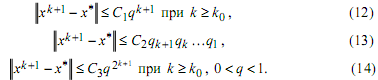
Для характеристики сходимости последовательности {xk}kϵN к f(x*) в ситуациях, аналогичных (9), (10), (11), используются аналогичные термины: линейная, сверхлинейная и квадратичная скорость сходимости.
Для невыпуклых задач численные методы оптимизации обычно позволяют отыскивать лишь локальные решения, а, точнее говоря, стационарные точки. Задача отыскания глобального решения в общем случае чрезвычайно сложна. Алгоритмы глобальной оптимизации требуют больших затрат вычислительных ресурсов даже для функций одной переменной. Получение же достаточно точного решения многомерных задач глобальной оптимизации с помощью существующих в настоящее время численных методов оказывается вообще невозможным. Установление факта сходимости и оценка скорости сходимости дают существенную информацию о выбранном методе минимизации. Прежде всего, требования, которые приходится накладывать в теореме о сходимости на минимизируемую функцию, показывают область применимости метода. Часто в теоремах о сходимости в явном виде формулируются требования к начальному приближению. Наконец, анализ скорости сходимости дает полезную количественную и качественную характеристику изучаемого метода оптимизации.
В то же время реальный процесс оптимизации не может быть бесконечношаговым, что существенно ограничивает применимость теорем о сходимости на практике. Кроме того, в ряде случаев предположения этих теорем труднопроверяемы. Поэтому при выборе подходящего метода решения реальных задач приходится во многом руководствоваться здравым смыслом, опытом, интуицией, а также результатами численных экспериментов. Для задания конкретного вычислительного алгоритма бесконечношаговый метод необходимо дополнить условием остановки. Условие остановки может определяться имеющимися в наличии вычислительными ресурсами. Например, может быть задано число вычислений предусмотренных алгоритмом характеристик минимизируемой функции f . Остановка может производиться и подостижении заданной точности решения задачи, например, на основе оценок (12)-(14). Однако при решении реальной задачи трудно оценить истинную точность. Так, константы, фигурирующие в оценках (12)-(14), обычно неизвестны. Поэтому о достижении заданной точности приходится судить по косвенным признакам.
На практике часто используются следующие условия остановки:
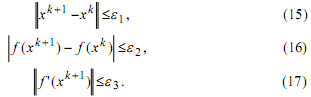
До начала вычислений выбирается одно из условий (15)-(17) и соответствующее ему малое εi > 0, i=1,2,3 . Вычисления прекращаются после (k+1) -го шага, если впервые оказывается выполненным выбранное условие остановки. На практике также используются критерии, состоящие в одновременном выполнении двух из условий (15)-(17) или всех трех условий. Ясно, что критерий (17) относится лишь к задачам безусловной оптимизации. Его выполнение означает, что в точке xk+1 с точностью ε3 выполнено условие стационарности. В задаче условной оптимизации критерий (17) следует заменить на критерий «ε -стационарности», соответствующий данной задаче.
Вместо условий (15)-(17), основанных на понятии абсолютной погрешности, можно использовать аналогичные критерии, основанные на понятии относительной погрешности:
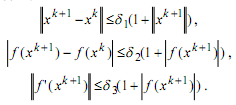
Отметим, что выполнение указанных критериев и других подобных им эвристических условий остановки не гарантирует достижения необходимой точности решения задачи.
В методах спуска направление движения к минимуму на каждом шаге выбирается из числа направлений убывания минимизируемой функции.
Говорят, что вектор h задает направление убывания функции f в точке x , если f(x+ah)<f(x) при всех достаточно малых a>0 . Сам вектор h также называют иногда направлением убывания. Множество всех направлений убывания функции f в точке x будем обозначать через U(x,f) . Таким образом, если любой достаточно малый сдвиг из x в направлении вектора h приводит к уменьшению значения функции f , то h ϵ U(x,f). Заменив неравенство, фигурирующее в определении направления убывания, на противоположное, получим определение направления возрастания.
В дальнейшем нам понадобятся следующие достаточный и необходимый признаки направления убывания функции.
Лемма 4. Пусть функция f дифференцируема в точке x ϵ Rn . Если вектор h удовлетворяет условию
(f’(x),h)<0 , (18)
то h ϵ U(x,f). Если h ϵ U(x,f), тогда
(f’(x),h)≤0. (19)