23. Численные методы решения задач линейного программирования. Геометрическая интерпретация прямого симплекс-метода.
Рассмотрим
б.д.р.
задачи P. ПустьB – его базисная матрица,
а N, соответственно, небазисная матрица.
Обозначим через П гиперплоскость,
натянутую на расширенные вектора базиса
,
и проходящую через начало координат.
Эта гиперплоскость однозначно определяется
бази-сом B и ее направляющий вектор
есть решение следующей системы
урав-нений
следовательно,
.
Оценки замещения симплекс-таблицы,
соответствующей б.д.р.
,
образуют вектор
.
Таким образом, если на первом шаге
итерации симплекс-таблица, соответствующая
б.д.р.
,
является двойственно допустимой,
тоесть
,
то вектор y является допустимым решением
двойственной задачи, тогда
и
– оптимальные решения. Их геометрическая
интерпретация содержится в предыдущем
параграфе. Если существует номер s такой,
что
,
то это означает, что
недопустимое решение двойственной
задачи, то есть симплекс-таблица не
двойственно допустима, а
неоптимальное решение. Геометрически
это эквивалентно тому, что вектор
расположен
ниже гиперплоскости П.
Рассмотрим конус
,
натянутый на вектора
:
.
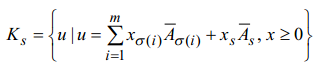Если коэффициенты замещения
,
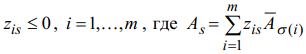то множество
содержит луч, исходящий из точки
.
Это следует из существования
параметрического семейства векторов
,
которое использовалось при обосновании
симплекс-метода. В этом случае задача
(1)-(3) не имеет оптимального решения.
Заметим, что это возможно тогда и только
тогда, когда конус
содержит полуось
.
Если конус
не содержит полуось
,
то тогда
и множество
является отрезком, который в вырожденном
случае может оказаться точкой. Если
задача (1)-(3) невырож-денная,то отрезок
отличен от точки. Его крайняя верхняя
точка является образом базисного
допустимого решения
и лежит на грани
образованной векторами
,
так как
.
Это означает, что эта грань есть
пересечение конуса
с гиперплоскостью П. Тогда нижняя точка
отрезка
является геометрическим образом нового
базисного допустимого решения
и лежит на грани, порожденной векторами
другими словами,
– новый базис, образованный векторами
.
Точки пересечения конуса
и
прямой Q являются геометрическими
образами решений, полученных из базисно
допустимого решения x элементарным
преобразованием, которое определяется
вектором
.
24. Численные методы условной оптимизации. Метод возможных направлений.
Методы безусловной оптимизации можно использовать для решения экс-тремальных задач условной оптимизации. Для этого необходимо доработать эти методы таким образом, чтобы учитывались ограничения задачи. В этом параграфе рассмотрен один из таких методов – методвозможных направлений.
Пусть имеется точка, удовлетворяющая ограничениям задачи. Выберем возможное направление движения, то есть такой ненулевой вектор, что
1. малое перемещение в этом направлении не выводит за пределы множе-ства допустимых решений;
2. целевая функция строго убывает в этом направлении.
Затем осуществляется перемещение в выбранном направлении до получения нового допустимого решения с лучшим значением целевой функции. Пред-ставленный ниже алгоритм был разработан голландским математиком Зой-тендейком [2, 3, 6], который предложил выбирать направление спуска из пересечения конусов возможных направлений и направлений убывания целевой функции. Особенность метода заключается в учете нелинейности ограниче-ний и в сравнении направлений не только по локальной скорости убывания целевой функции, но и по длинам шагов, которые удастся сделать вдоль них.
Представленный ниже алгоритм предназначается для поиска экстремума при наличии ограничений только типа неравенств. Рассмотрим задачу
