
- •Элементы выпуклого анализа.
- •Начальные сведения о численных методах оптимизации.
- •4.Сходимость методов оптимизации.
- •5.Метод покоординатного спуска.
- •6.Метод случайного поиска. Алгоритм с возвратом при неудачном шаге.
- •7. Метод случайного поиска. Алгоритм наилучшей пробы.
- •8. Метод случайного поиска. Алгоритм статистического градиента.
- •9. Метод случайного поиска. Алгоритм покоординатного обучения.
- •10. Градиентный метод. Метод с постоянным шагом.
- •11. Градиентный метод. Метод с дроблением шага.
- •12. Градиентный метод. Метод наискорейшего спуска.
- •13. Метод Ньютона
- •14. Численные методы решения задач линейного программирования. Прямой симплекс-метод. Базис и базисное решение.
- •15. Численные методы решения задач линейного программирования. Прямой симплекс-метод. Элементарные преобразования. Симплекс-таблицы.
- •16. Численные методы решения задач линейного программирования. Прямой симплекс-метод. Алгоритм симплекс-метода.
- •17. Численные методы решения задач линейного программирования. Модифицированный симплекс-метод.
- •18. Численные методы решения задач линейного программирования. Лексикографический прямой симплекс-метод
- •19. Численные методы решения задач линейного программирования. Двойственный симплекс-метод.
- •20. Численные методы решения задач линейного программирования. Двойственный симплекс-метод.
- •22. Численные методы решения задач линейного программирования. Геометрическая интерпретация задач линейного программирования
- •23. Численные методы решения задач линейного программирования. Геометрическая интерпретация прямого симплекс-метода.
- •24. Численные методы условной оптимизации. Метод возможных направлений.
- •25. Численные методы условной оптимизации. Метод Келли и метод секущих плоскостей.
- •26. Численные методы условной оптимизации. Первый (циклический) алгоритм Гомори.
- •27. Численные методы условной оптимизации. Метод ветвей и границ
- •28. Численные методы условной оптимизации. Метод ветвей и границ для решения задач нелинейного программирования
- •29. Численные методы условной оптимизации. Метод внешних штрафов
- •30.Численные методы условной оптимизации. Метод внутренних штрафов или метод барьерных функций
- •31.Муравьиный алгоритм.
- •32.Генетические алгоритмы.
- •33.Задачи классического вариационного исчисления. Постановка задачи классического вариационного исчисления
- •Сильный и слабый экстремум в задачах классического вариационного исчисления.
- •Допустимые управления и управляемые процессы в задачах оптимального управления. Оптимальные процессы
- •Элементарный вывод необходимых условий экстремума для простейших задач классического вариационного исчисления
- •Задачи оптимального управления. Постановка задачи оптимального управления
- •Формулировка принципа максимума для линейной задачи быстродействия
- •Доказательство принципа максимума для линейной задачи быстродействия.
- •Достаточность принципа максимума
20. Численные методы решения задач линейного программирования. Двойственный симплекс-метод.
Существуют следующие числовые методы решения задач линейного программирования:1) прямой симплекс-метода 2) модифицированный симплекс-метод 3) лексикографический прямой симплекс-метод 4) двухфазовый симплекс-метод 5) двойственный симплекс-метод 6) лексикографический двойственный симплекс-метод
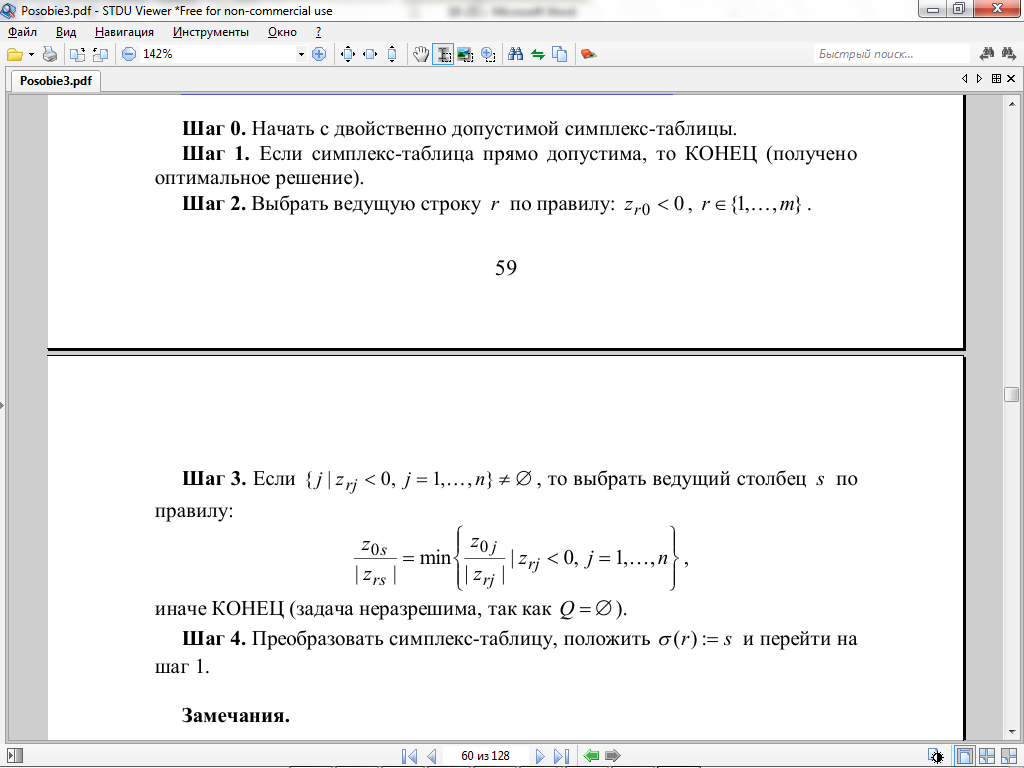
Фактически в симплекс-методе на каждой итерации рассматриваются базисные решения прямой и двойственной задач с равными значениями целевых функций. Алгоритм организован таким образом, что на нулевом шаге 1-ой итерации выбирается прямо допустимый базис и затем с помощью элементарных преобразований, сохраняющих прямо допустимость, происходит перебор базисов. В тот момент, когда обнаруживается двойственно допустимый базис или неразрешимость задачи, процесс останавливается.
Теперь мы можем сформулировать идею нового алгоритма, который назовем двойственным симплекс-методом. На нулевом шаге 1-ой итерации выбирается начальный двойственно допустимый базис и затем с помощью элементарных преобразований, сохраняющих двойственную допустимость, происходит перебор базисов. В тот момент, когда обнаруживается прямо допустимый базис или неразрешимость задачи, процесс останавливается.В приведенном ниже описании алгоритма этого метода предполагается,
что используются та же форма симплекс-таблицы и то же элементарное преобразование, что и в параграфе 1. Под s(i) , i =1,...,m , как и прежде, понимается набор номеров базисных столбцов (переменных).
21.Численные методы решения задач линейного программирования. Лексикографический двойственный симплекс-методСуществуют следующие числовые методы решения задач линейного программирования:1) прямой симплекс-метода 2) модифицированный симплекс-метод 3) лексикографический прямой симплекс-метод 4) двухфазовый симплекс-метод 5) двойственный симплекс-метод 6) лексикографический двойственный симплекс-метод
Пусть B – двойственно допустимый базис, S’ ={t (1)….,t (l)}, l = n - m , –
множество
номеров небазисных переменных, а S –
множество номеров базисных переменных.
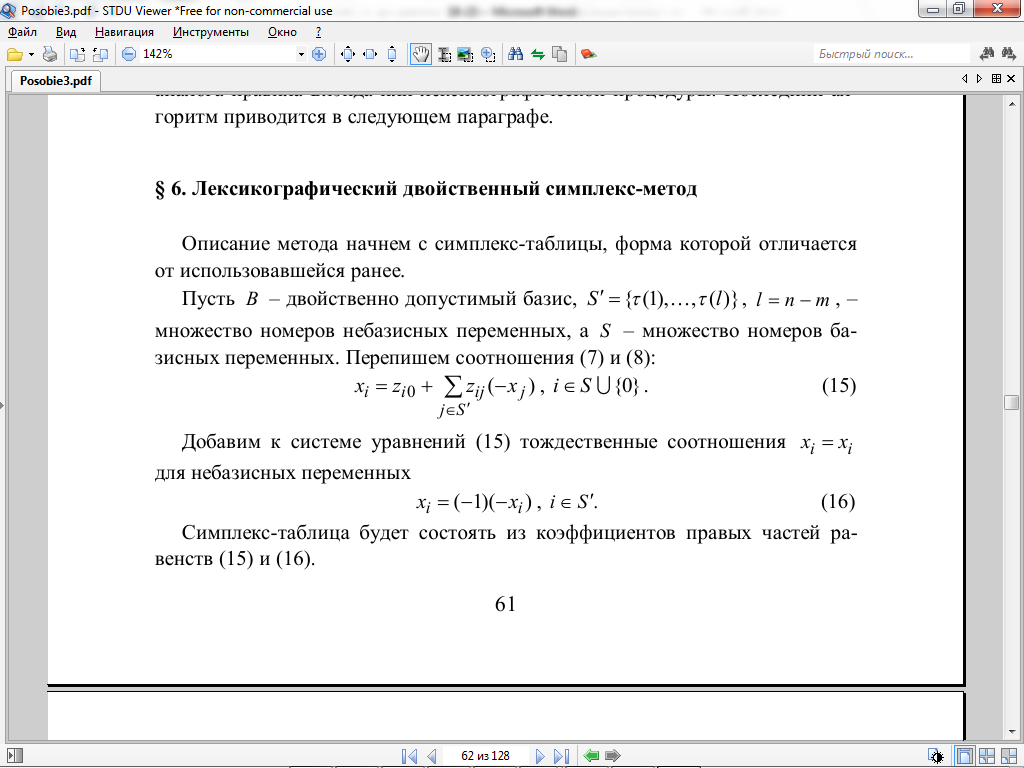
Добавим
к системе уравнений тождественные
соотношения xi
= xi
для небазисных
переменных
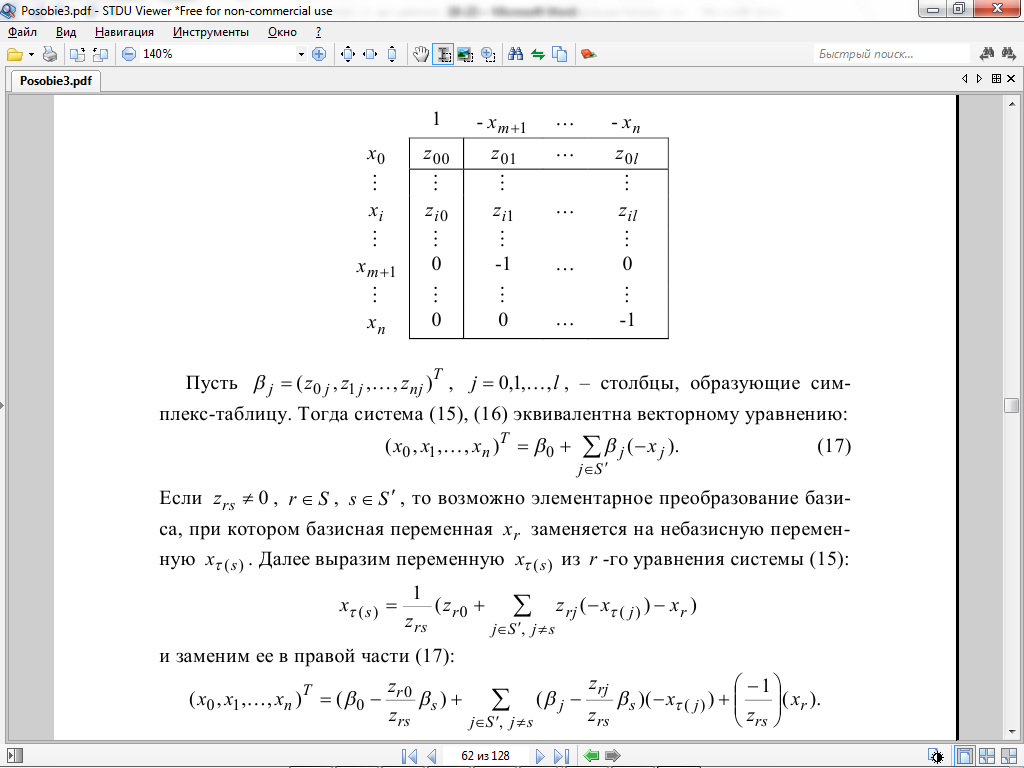
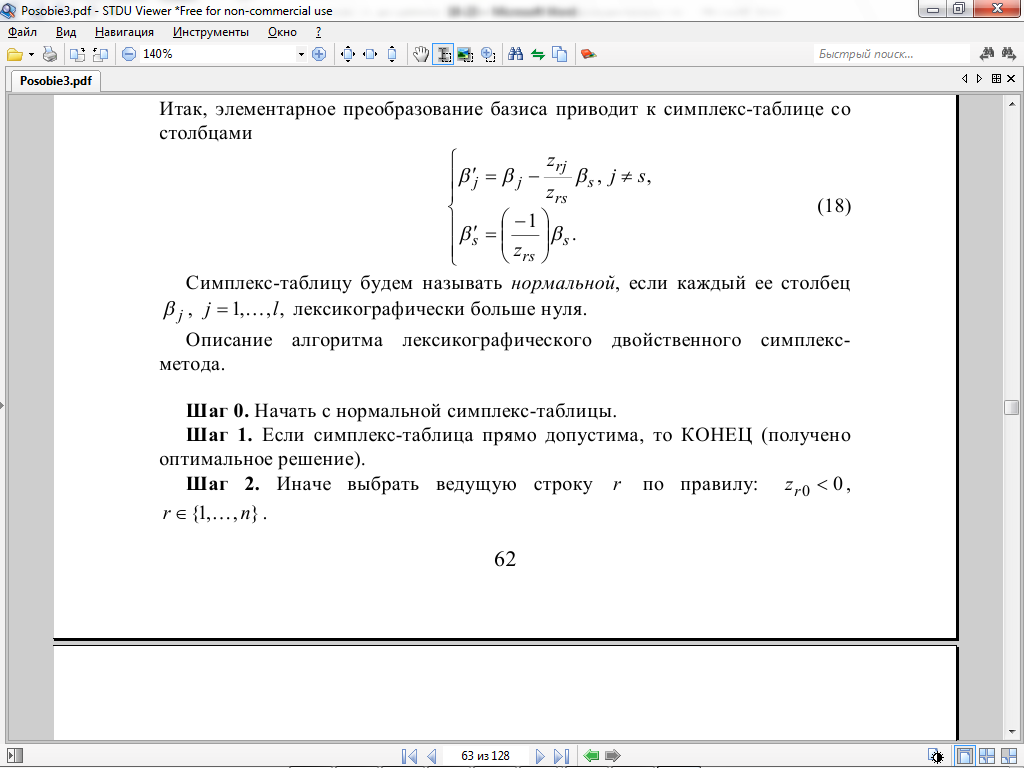
![]() Симплекс-таблица будет состоять из
коэффициентов правых частей равенств
Симплекс-таблица будет состоять из
коэффициентов правых частей равенств
22. Численные методы решения задач линейного программирования. Геометрическая интерпретация задач линейного программирования
Приведем геометрическую интерпретацию задач линейного программирования применительно к следующей паре взаимодвойственных задач, которые обозначим, соответственно, через P и D:

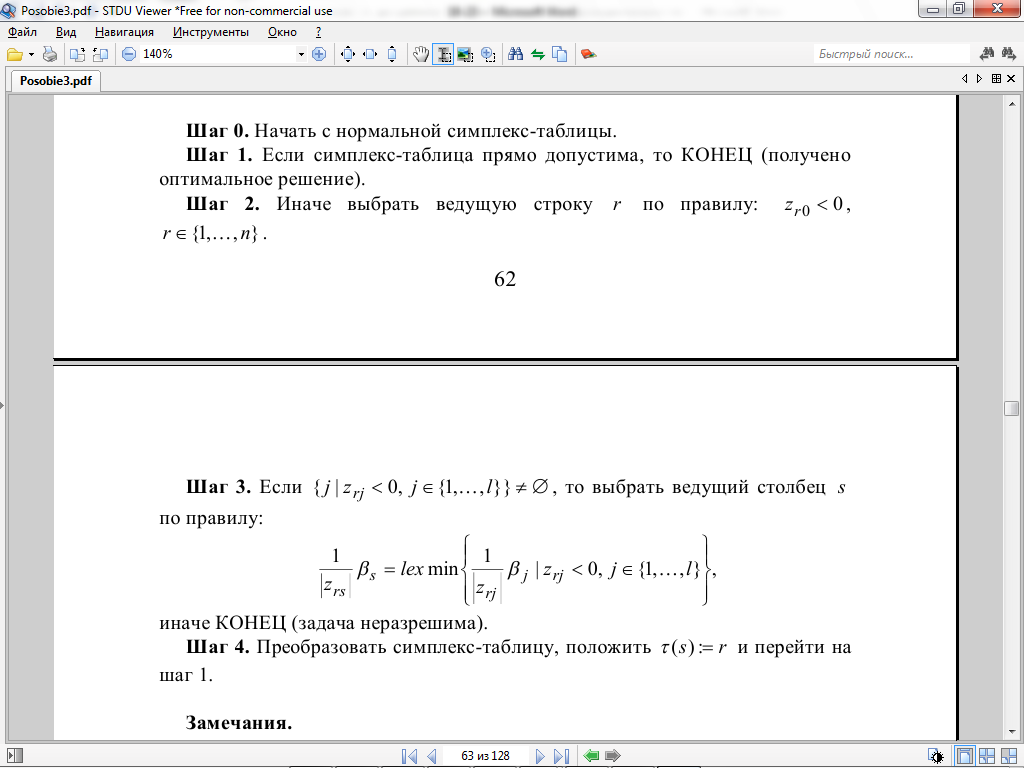
Обозначим через
![]() ,
расширенные вектор-столбцы матрицы А,
а через
,
расширенные вектор-столбцы матрицы А,
а через
![]() – расширенный вектор правых частей
ограничений прямой задачи. Множество
K,
содержащее с любой своей точкой x
все точки
– расширенный вектор правых частей
ограничений прямой задачи. Множество
K,
содержащее с любой своей точкой x
все точки
![]() при
при![]() ,
называется конусом.
,
называется конусом.
Определим
линейное преобразование:
![]()
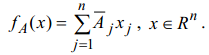
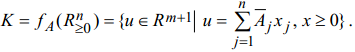
Пусть Очевидны следующие свойства множества K:
1. K – выпуклый конус.
2.
Вектор
![]() и
является его вершиной.
и
является его вершиной.
3.
K порожден конечным числом векторов
![]() то
есть является множеством точек вида
то
есть является множеством точек вида
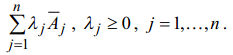
Чтобы пояснить введенное определение конуса K, рассмотрим следую-щую задачу линейного программирования:
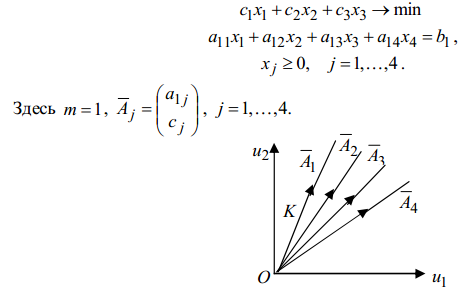
На рисунке
приведено множество K
для данной задачи. Очевидно, что конус
K
порожден крайними лучами, образованными
векторами
![]() Рассмотрим систему уравнений:
Рассмотрим систему уравнений:
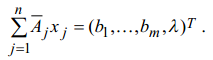
Будем считать,
что вектор c коэффициентов целевой
функции прямой задачи P не является
линейной комбинацией векторов
![]() ,
так как в противном случае любое
допустимое решение является оптимальным.
Тогда
,
так как в противном случае любое
допустимое решение является оптимальным.
Тогда
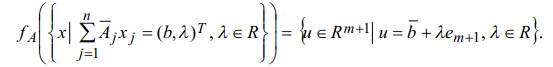
Обозначим последнее
множество через Q.
Оно является прямой в пространстве
![]() ,
которая проходит через точку
,
которая проходит через точку
![]() параллельно оси
параллельно оси
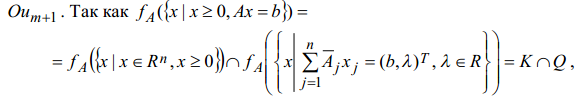
то образом множества
допустимых решений задачи P при отображении
![]() является пересечение конуса K и прямой
Q. Таким образом, задача P сводится к
поиску «крайней» точки пересечения
прямой Q и конуса K, то есть точки с
наименьшей последней координа-той.
является пересечение конуса K и прямой
Q. Таким образом, задача P сводится к
поиску «крайней» точки пересечения
прямой Q и конуса K, то есть точки с
наименьшей последней координа-той.

На
рис. 2 точка M – крайняя точка пересечения
![]() ,
является образом оптимальных решений
рассмотренной выше задачи ЛП. Приведем
интерпретацию задачиD. Пусть
,
является образом оптимальных решений
рассмотренной выше задачи ЛП. Приведем
интерпретацию задачиD. Пусть
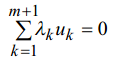
уравнение
гиперплоскости, проходящей через начало
координат. Направ-ляющий вектор
![]() гиперплоскости определен с точностью
до ненулевого множителя. Будем считать,
что
гиперплоскости определен с точностью
до ненулевого множителя. Будем считать,
что
![]() .
Другими словами, мы не рассматриваем
гиперплоскости содержащие ось
.
Другими словами, мы не рассматриваем
гиперплоскости содержащие ось
![]() .
Следовательно, существует взаимнооднозначное
соответствие между гиперплоскостями,
.
Следовательно, существует взаимнооднозначное
соответствие между гиперплоскостями,
проходящими через
ноль, не содержащими ось
,
и их направляющими векторами
.
Пусть
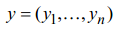 – допустимое решение задачи D, а
– допустимое решение задачи D, а
![]() – гиперплоскость, определяемая уравнением
– гиперплоскость, определяемая уравнением
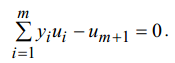
Подставим![]() в
это уравнение. Так как y является
допустимым решением задачи D, то 0
в
это уравнение. Так как y является
допустимым решением задачи D, то 0
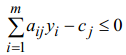 .
Поскольку конус K порожден векторами
,
K ле-жит «над» гиперплоскостью
.
Поскольку конус K порожден векторами
,
K ле-жит «над» гиперплоскостью
![]() ,
то есть по ту же сторону от гиперплоскости,
что и векто
,
то есть по ту же сторону от гиперплоскости,
что и векто
![]()
Пусть
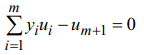 –
произвольная гиперплоскость, проходящая
че-рез O и не содержащая ось
.
Если конус K располагается «над»
ги-перплоскостью, то есть для любой
точки
–
произвольная гиперплоскость, проходящая
че-рез O и не содержащая ось
.
Если конус K располагается «над»
ги-перплоскостью, то есть для любой
точки
![]() справедливо
справедливо
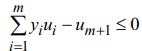 ,
тогда для любого расширенного вектора
условий
выполняется
,
тогда для любого расширенного вектора
условий
выполняется
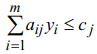 ,
следовательно,
,
следовательно,
![]() является допустимым
является допустимым
решением задачи D. Итак, геометрическим образом множества допустимых решений задачи D является совокупность гиперплоскостей, содержащих начало координат, не содержащих ось и расположенных «под» конусом K. Это соответст-вие является взаимнооднозначным и определяется уравнениями (21).
Пусть![]() .
Тогда из определенияQ и (21) имеем
.
Тогда из определенияQ и (21) имеем
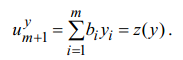
Следовательно,
значение целевой функции двойственной
задачи на допустимом решении равно
расстоянию от точки пересечения прямойQ
и гиперплоскости
до
гиперплоскости
![]()
Таким образом,
с геометрической точки зрения двойственная
задача заключается в отыскании такой
гиперплоскости, которая содержит начало
координат, не содержит ось
![]() ,
расположена «под» конусом K и пересекает
Q в «наивысшей точке» в смысле порядка
на оси
.
,
расположена «под» конусом K и пересекает
Q в «наивысшей точке» в смысле порядка
на оси
.
