30.2. Расчеты и статистическая обработка результатов

30.2.1. MathCad

MathCAD является представителем нового поколения программных средств и предназначен для инженерных и математических расчетов. Он чрезвычайно прост в использовании и лёгок в освоении. Его интерфейс настолько удобно сделан, что пользователь работает с рабочим листом программы, как с листом бумаги, где он пишет формулы и математические выражения в их привычной нотации. Mathcad может выполнять вычисления любой степени сложности и ограничен лишь техническими возможностями вашей техники. Помимо численных расчетов, он может выполнять и символьные вычисления (здесь это называется "символьная математика"). Имеются обширные графические возможности. Помимо традиционных типов графиков можно строить поверхности, линии уровня и векторные поля.

Очень интересное и полезное изобретение разработчиков заключается в создании электронной книги, она называется "Центр ресурсов". В книге помещены многочисленные примеры решения типичных задач, причём их можно не только просматривать, но и переносить на свой рабочий лист обычной операцией копирования или буксировкой. Таких электронных книг по различным областям науки и техники существует великое множество и их можно извлекать с серверов Internet.

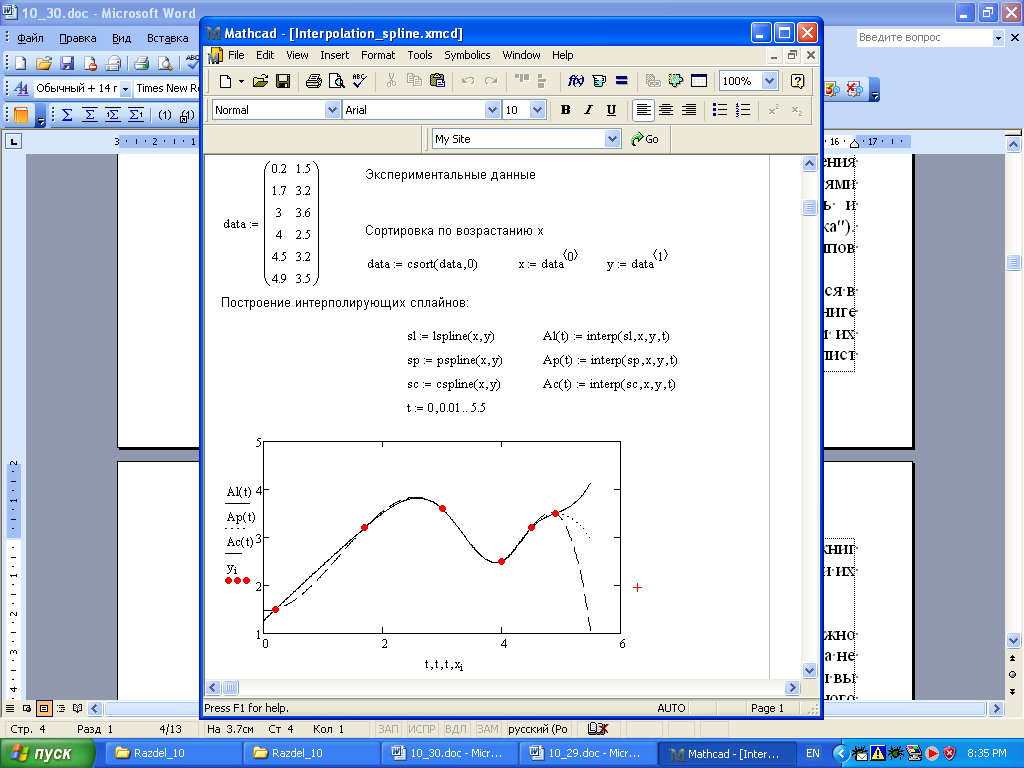
Рис. 30.2. Решение задачи сплайн – интерполяции экспериментальных данных в Mathcad

Mathcad Explorer. При расчетах и чтении MathCAD документов можно использовать бесплатную программу MathCAD Explorer, но эта программа не позволяет сохранить результаты расчетов. Последнюю версию программы вы можете скачать или с сайта MathSoft, или с образовательного математического сайте http://www.Exponenta.ru.

Ниже приведены еще две более специализированные программы, предназначенные для графического представления и статистической обработки различных данных. Программы легко интегрируются с MathCAD и могут использоваться с ним совместно дополняя друг друга.

S-Plus - мощная программа для статистической обработки и графического представления результатов измерений. Программа хорошо интегрируется с MathCAD и позволяет получать графическое представление расчетов в виде, готовом для публикации в отчете или дипломном проекте. Axum (по существу, облегченная версия S-Plus). Демонстрационные версии всех программ можно скачать на сайте MathSoft (http://www.mathsoft.com).

30.2.2. Matlab - Scilab - Octave

Системы компьютерной математики (СКМ) сегодня стали важнейшим рабочим инструментом во многих фундаментальных и прикладных науках. Их использование существенно облегчает исследователю жизнь, а зачастую вообще является единственным способом получения каких-либо значимых результатов. Однако для большинства отечественных пользователей коммерческие СКМ высшего класса (MathCAD, Mathematica, Maple и др.) слишком дороги. Разумным и фактически безальтернативным выходом представляется бесплатное ПО, и оказывается, в нем также встречаются весьма качественные разработки, одной из которых является Scilab.

Пакет Scilab является свободно распространяемой (вместе с исходными кодами) системой компьютерной математики. До недавнего времени он разрабатывался исследовательскими институтами INRIA и ENPC (оба находятся во Франции), а с мая 2003 г. поддержку продукта взял на себя специально созданный для этой цели Scilab Consortium, с Web-узла которого (http://scilabsoft.inria.fr/) можно загрузить последнюю версию программы и полный комплект документации (на момент подготовки материала была доступна версия 4.0). Scilab выпускается для операционных систем Windows (любая 32-разрядная версия), наиболее популярных Unix/Linux и не нуждается в больших системных ресурсах: инсталляционный модуль имеет размер до 20 MB, а для установки требуется немногим более 40 MB.

Пакет не случайно имеет название, созвучное с Matlab -- одной из наиболее мощных коммерческих СКМ. У обоих приложений немало общего -- от интерфейса и принципа взаимодействия с пользователем через командную строку до синтаксиса языка. Таким образом, Scilab можно рассматривать как облегченный вариант Matlab, который, впрочем, сохраняет основные возможности последнего.

Scilab является типичным командным интерпретатором и структурно состоит из интерпретирующей системы, принимающей команды пользователя и возвращающей результаты, и двух библиотек: собственных функций и дополнительных -- на языках С и Fortran.

Хотя Scilab является бесплатным продуктом, его вычислительные возможности, обеспеченные приблизительно тысячью встроенных функций, вполне соответствуют СКМ профессионального уровня.

Функции системы, относящиеся к некоторым прикладным областям математики и техники, собраны в дополнительные пакеты расширений (так называемые toolboxes). Одни из них применяются достаточно широко (как, скажем, методы численного решения краевых задач для систем дифференциальных уравнений, линейное и квадратичное программирование), другие имеют узкую специфическую направленность. Из последних назовем пакеты для цифровой обработки сигналов, анализа динамических систем, оптимизации со специальными ограничениями.

Scilab является надежной и мощной платформы для создания недорогих, но вполне конкурентоспособных решений в области обработки данных, численной реализации алгоритмов и визуализации. Поэтому если перед вами стоят подобные задачи, стоит обратить пристальное внимание на эту неординарную и доступную вычислительную систему.

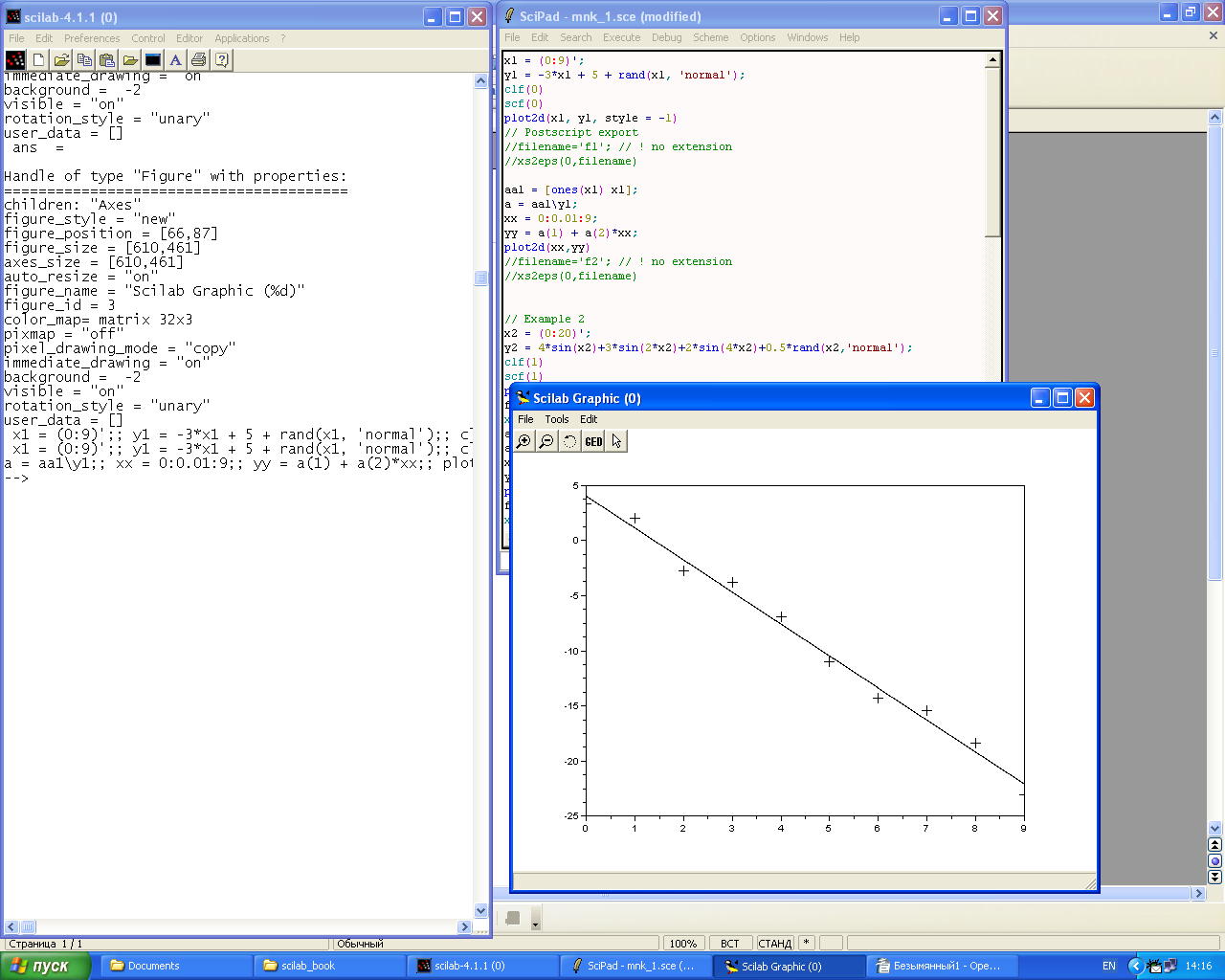
Рис. 30.3. Рабочее окно, окно встроенного редактора программ и графическое окно Scilab.

Octave - интерактивная программная система с открытым исходным кодом для числовых вычислений и построения графиков. Она предназначена в основном для матричных вычислений: решения систем уравнений, вычисления собственных векторов и собственных значений и так далее. Во многих реальных технических задачах данные могут быть представлены как матрицы и векторы, и решение этих задач сводится к этим формам решения. Кроме того, Octave может представлять данные различным образом, а также имеет свой собственный язык программирования, который позволяет расширять систему. Об Octave можно говорить как об очень мощном, программируемом, графическом калькуляторе. Octave облегчит Вам решение широкого круга числовых задач и оставит больше времени на эксперимент и обдумывание более широкой проблеме.

Ценность Octave увеличивается еще и в связи с тем, что синтаксисом она совместима с MATLAB, который обычно используется в промышленности и науке.

Octave разработана для решения математических задач численно. Это означает, что Octave может не всегда давать точное решение задачи, и ее не должно путать с программами типа Mathematica или Maple, которые дают символьные решения, делая алгебраические манипуляции. Это не означает, что Octave лучше или хуже - она используется для решения своего круга задач. Самые реальные математические проблемы (особенно технические!) не имеют четких символьных решений.

Рис. 30.4. Программа Octave.

Octave и MATLAB широко используются инженерами и учеными и в промышленности и в науке для того, чтобы выполнять числовые вычисления, и для того, чтобы разработывать и проверять математические алгоритмы. Например, NASA использует ее для разработки космических кораблей; Jaguar Racing - чтобы отображать и анализировать данные, переданные от автомобилей Formula 1; Sheffield University - для разработки программного обеспечения для распознаваия злокачественных клеток.