33.6. Регрессия

33.6.1. Выбор вида математической модели

Как мы выяснили, через n точек можно всегда провести кривую, аналитически выражаемую многочленом (n - 1) -й степени. Этот многочлен называют интерполяционным. И вообще, замену функции на функцию так, что их значения совпадают в заданных точках называют интерполяцией.

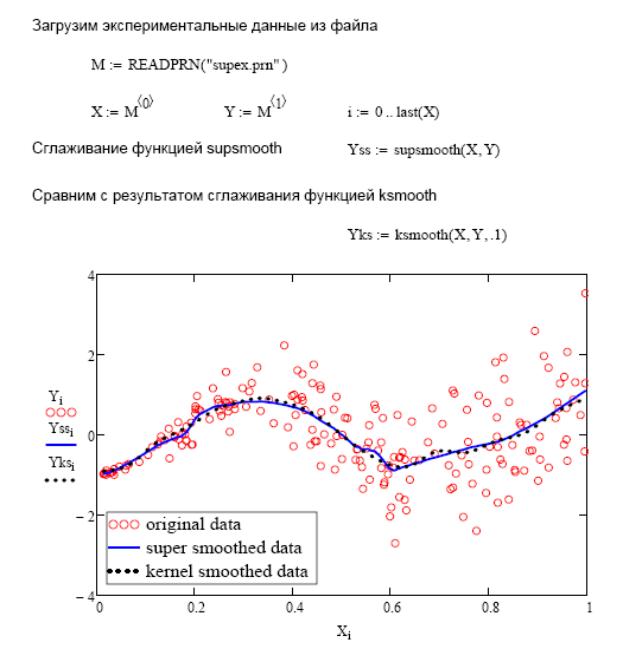
Рис. 33.13. Сглаживание функцией supsmooth.

Однако такое решение проблемы не является удовлетворительным, поскольку из-за случайных ошибок измерения и влияния на измерения значений помех и шумов в устройстве. Так что

, (33.11)

где - некоторая случайная ошибка. Поэтому требуется провести кривую так, чтобы она в наименьшей степени зависела от случайных ошибок. Эта задача называется сглаживанием (аппроксимацией) экспериментальной зависимости и часто решается методом наименьших квадратов. Сглаживающую кривую называют аппроксимирующей.

Как правило, регрессия очень эффективна, когда заранее известен (или, по крайней мере, хорошо угадывается) закон распределения данных. Задача выбора вида функциональной зависимости - задача не формализуемая, так как одна и та же кривая на данном участке примерно с одинаковой точностью может быть описана самыми различными аналитическими выражениями. Так, например, U - образная кривая может быть описана участком параболы, гиперболы, эллипса или синусоиды. Рациональный выбор того или иного аналитического описания может быть обоснован лишь при учете определенного перечня требований.

Главное требование к математической модели - это удобство ее последующего использования. Основное, что обеспечивает удобство математического выражения, - его компактность. Например, известно, что любую функцию можно описать многочленом . Но если же оказывается возможным с приемлемой точностью описать ее одночленом вида , и т. п., то ясно, что такое компактное представление много лучше. Таким образом, компактность модели достигается удачным выбором элементарных функций, обеспечивающих хорошее приближение при малом их числе.

Другое весьма желательное (но не всегда достижимое) требование – это содержательность, иначе говоря, интерпретируемость предлагаемого аналитического описания. Как правило, это достигается путем придания определенного смысла константам или функциям, входящим в найденную математическую модель. Отсюда следует важное практическое обстоятельство. Даже в наше время широкого использования компьютеров в научных исследованиях принятие решения о выборе той или иной математической модели остается за человеком - исследователем и не может быть передано компьютеру. Только человек, а не компьютер, знает, для чего будет в дальнейшем использоваться эта модель, на основе каких понятий будут интерпретированы ее параметры и т. д.

Если подбор вида аппроксимирующей функции - процесс не формальный и не может быть полностью передан компьютеру, то расчет параметров аппроксимирующей функции выбранного вида - операция чисто формальная и ее следует осуществлять на компьютере. Более того, это трудный и утомительный процесс, в котором человек не застрахован от ошибок, а компьютер выполнит его быстрее и качественнее.

В общем случае этот расчет состоит в решении системы нелинейных уравнений. В частных случаях это может быть система уравнений линейных относительно искомых параметров, система уравнений, которые после ряда преобразований сводятся к линейным и, наконец, когда уравнения системы не сводятся к линейным. Так, например, если известны координаты и для n экспериментальных точек, а для аппроксимации принята модель в виде многочлена , то расчет неизвестных коэффициентов, т. е. искомых по известным координатам n точек сводится к решению системы уравнений, линейных относительно коэффициентов.

Как видно из этого примера, число независимых уравнений системы равно числу n поставленных опытов. С другой стороны, для определения k коэффициентов необходимо не менее k независимых уравнений. Но если число n поставленных опытов и число независимых уравнений равно числу искомых коэффициентов, то решение системы единственно, а следовательно, случайно, так как точно соответствует случайным значениям исходных данных. При числе опытов n, большем, чем число k искомых коэффициентов, число независимых уравнений системы избыточно. Из этих уравнений в разных комбинациях можно составить несколько систем уравнений, каждая из которых в отдельности даст свое решение. Но между собой они будут несовместимы. Каждое решение будет соответствовать своей аппроксимирующей функции. Если все их построить на графике, то получим целый пучок аппроксимирующих кривых.

Это открывает при n > k совершенно новые возможности. Во-первых, этот пучок кривых показывает форму и ширину области неопределенности проведенного эксперимента. Во-вторых, может быть произведено усреднение всех найденных кривых. Полученная усредненная кривая будет гораздо точнее и достовернее описывать исследованное явление, так как она в значительной степени освобождена от случайных погрешностей, приводящих к разбросу отдельных экспериментальных точек.

Таким образом, проведение большего числа опытов n, чем минимально необходимое для расчета коэффициентов n = k, позволяет определить область неопределенности по фактическим данным эксперимента и одновременно существенно уменьшить случайную погрешность окончательного результата путем усреднения.