
- •Раздел 10. Основы анализа экспериментальных данных
- •29.2. Классификация погрешностей
- •30. Обзор программного обеспечения для выполнения анализа, обработки и представления экспериментальных данных
- •30.1. Математические (символьные) вычисления
- •30.2. Расчеты и статистическая обработка результатов
- •30.2.1. MathCad
- •30.2.2. Matlab - Scilab - Octave
- •30.3. Построение графиков
- •30.3.1. Sigma Plot
- •30.3.2. Origin
- •30.3.3. Gnuplot
- •30.4. Работа с текстом
- •30.4.1. Ms Word
- •30.4.2. OpenOffice.Org
- •31. Анализ результатов измерений случайной величины.
- •31.1. Гистограмма. Эмпирическое распределение результатов наблюдений
- •31.2. Результат измерения. Доверительный интервал
- •31.3. Нормальное или гауссово распределение
- •31.4. Выборочные дисперсия и среднеквадратичное отклонение
- •31.5. Среднеквадратичная ошибка среднего.
- •31.6. Приборная погрешность. Класс точности прибора.
- •31.7. Сложение случайной и приборной погрешностей. Полная погрешность измерения
- •31.8. Запись и округление результата измерения
- •32. Ошибки косвенных измерений
- •32.1. Функция одной переменной
- •32.2. Функция нескольких переменных
- •32.3. Ошибки и методика эксперимента
- •33. Анализ результатов совместных измерений
- •33.1. Цель и особенности эксперимента по определению функциональной зависимости
- •33.2. Некоторые определения
- •33.3. Интерполяция
- •33.3.1. Глобальная интерполяция
- •33.3.2. Локальная интерполяция
- •33.3.2.1. Кусочно-линейная интерполяция
- •33.3.2.2. Интерполяция кубическими сплайнами
- •33.3.2.3. Интерполирование b-сплайнами
- •33.4. Экстраполяция
- •33.5. Сглаживание данных
- •33.6. Регрессия
- •33.6.1. Выбор вида математической модели
- •33.6.2. Метод наименьших квадратов.
- •33.6.2.1. Линейная зависимость.
- •33.6.2.2. Линеаризация
- •33.6.2.3. Полиномиальная регрессия
- •33.6.2.4. Регрессия линейной комбинацией функций
- •33.6.2.5. Регрессия общего вида.
31.7. Сложение случайной и приборной погрешностей. Полная погрешность измерения
Пусть
результаты наблюдений наряду со случайной
содержат и систематическую приборную
погрешность
,
которую можно считать постоянной в
течение времени проведения измерения,
так как характеристики прибора за это
время не успевают заметно измениться.
Наблюдаемые в опыте результаты наблюдений
будут при этом равны
![]() .
Наличие постоянной погрешности, вносимой
прибором в результаты наблюдений,
приводит к смещению выборочного среднего
.
Наличие постоянной погрешности, вносимой
прибором в результаты наблюдений,
приводит к смещению выборочного среднего
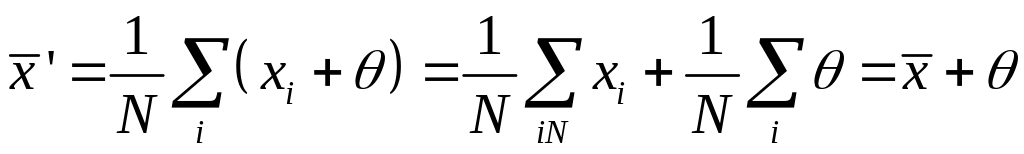 . (31.34)
. (31.34)
Однако ее наличие совершенно не влияет на случайную погрешность результата измерения.
Смещение
среднего и доверительного интервала
может привести к тому, что истинное
значение
измеряемой величины окажется за пределами
найденного доверительною интервала
![]() ,
как это показано на рис. 31.6.
,
как это показано на рис. 31.6.
Чтобы
этого не произошло, необходимо расширить
доверительный интервал на величину
верхней границы возможных значений
погрешностей прибора
.
В этом случае
![]() и результат измерения можно записать
в виде
и результат измерения можно записать
в виде
![]() , (31.35)
, (31.35)
где
![]() назовём полной погрешностью результата
измерения. Новый доверительный интервал
(
назовём полной погрешностью результата
измерения. Новый доверительный интервал
(![]() )
обязательно накроет истинное значение
,
так как
)
обязательно накроет истинное значение
,
так как
![]() (рис. 31.6). Отметим, что доверительная
вероятность, соответствующая найденному
таким образом доверительному интервалу,
будет превышать доверительную вероятность,
используемую для нахождения случайной
составляющей погрешности измерения.
(рис. 31.6). Отметим, что доверительная
вероятность, соответствующая найденному
таким образом доверительному интервалу,
будет превышать доверительную вероятность,
используемую для нахождения случайной
составляющей погрешности измерения.
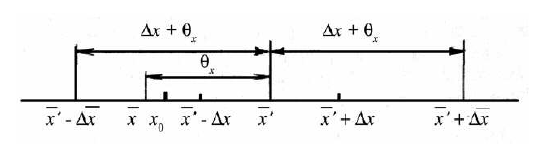
Рис. 31.6. К определению полной погрешности измерения
Указанный
способ суммирования погрешностей дает
максимальную верхнюю границу полной
погрешности результата измерения.
Однако маловероятно, что в данном
эксперименте полная погрешность примет
своё максимальное значение. Учитывая,
что, как правило, на практике приборная
погрешность, как отдельного прибора
(погрешности квантования и шкалы
прибора), так и в серии приборов изменяется
нерегулярным образом, оставаясь в
границах
![]() ,
полная погрешность результата измерения
с учетом неизвестности величины и знака
лежит в пределах
,
полная погрешность результата измерения
с учетом неизвестности величины и знака
лежит в пределах
![]() . (31.36)
. (31.36)
Сопоставляя это выражение с неравенством треугольника
![]() (31.37)
(31.37)
можно заключить, что в качестве разумной оценки полной погрешности результата измерения можно выбрать величину
![]() (31.38)
(31.38)
Строгое
рассмотрение суммирования случайной
и приборной погрешностей основано на
построении совместной функции плотности
распределения вероятности
![]() .
Будем считать, что в интервале (
)
все возможные значения приборной
погрешности равновероятны, то есть
приборная погрешность распределена
равномерно. Тогда совместная функция
распределения
представляет собой свертку нормального
(или распределения Стьюдента для
конечного числа наблюдений
)
и равномерного
.
Будем считать, что в интервале (
)
все возможные значения приборной
погрешности равновероятны, то есть
приборная погрешность распределена
равномерно. Тогда совместная функция
распределения
представляет собой свертку нормального
(или распределения Стьюдента для
конечного числа наблюдений
)
и равномерного
![]() законов распределения:
законов распределения:
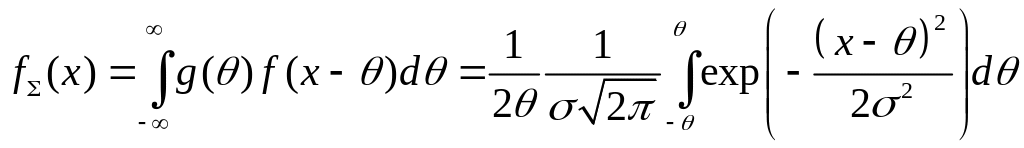 . (31.39)
. (31.39)
Можно построить доверительный интервал для совместной функции распределения случайной и приборной погрешностей. Полученное выражение для полной погрешности результата измерения хорошо (с точностью до 5%) аппроксимируется формулой.
Итоговая запись результата измерения будет иметь вид
![]() (31.40)
(31.40)
с
вероятностью
![]() ,
где
,
где
![]() - вероятность определения случайной
составляющей погрешности измерения.
- вероятность определения случайной
составляющей погрешности измерения.
