38. Основные св-ва пределов функций.

₁.если ф-я f(х) имеет в т.x_{0,то он единственный}

_{2.если ф-я f(х)імеет в т. x0 предел,то сущ. окресность в т. х0,в кот. Ф-я f(х) ограничена}

_{3.если у=С-пост. Ф-я,то}

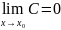
_{4.если , 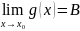,то а) lim(f±g)=A+B; б)(f*g)=A*B; в)f/g=A/B, B≠0}

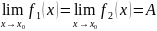_{5.если в окрестности в т. х0 выполняются нер-ва f1(x)≤f(x)≤f2(x) и} , то и

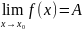
_{6.сохранение знака предела. Если 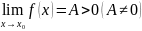,то сущ. Окрестность в т.x0 такая, что f(х)>0 (f(x) <0)при всех х из этой окресности.}

ел функции

39. Замечательные пределы

I замеч.предел: .докажем

Из рис.5:AB=sinx,BD=x,CD=tgx.

Для достаточ.малых пределов:sinx<x<tgx

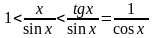,тогда

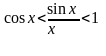,учитывая

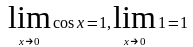
II Замечательный предел

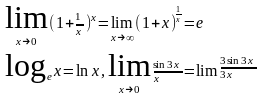
40-41.Непрерывные ф-ции.точки разрыва ,их классификация.Пусть дана ф-ция f(x),в кот.опред.точки промежутка – I и Xо. Ф-ция наз. непрерывной,если её предел равен знач.ф-ции в этой точке,т.е.

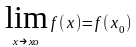
Пусть f(x) опред. в некот. окрестности т.Xo. Точку Xo наз.точкой разрыва ф-ции f(x).

Классификация точек разрыва:

Если Xo точка разрыва ф-ции и сущ. конечные пределы,то т.Xo явл. точкой

разрыва первого рода.

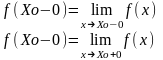
Величина f (Xo+0) - f (Xo-0) называется

скочком ф-ции в т.Xo. Если скачок равен 0 в т. разрыва.то Xo наз.точкой устронимого разрыва.Точка не явл. точкой I рода.наз. точкой II рода.Здесь под пределом понимается конечный предел: Свойства непрерывных функций:

1)если f(x)непрер. на отр.(a;b)то она ограничена на отрезке и прин. найб. и наймен. значение.2) если f(x) опред. и непрерывна на отрезке,то хотя бы одна т. С леж. м/у точ. А и В такая,что f(c)=0 .3)Если f(x) непрер. и прин. найб. и найм знач.,то для люб. С найдётся точка С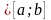 такая чтоf(c)=C

42. Дифференциал ф-ции и геом.Смысл

пусть ф.y=f(x) дифференн. в т. Xo Приращение предст.

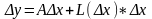
Дифференциал-главная линейная относитель. 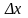,часть приращ. ф-ции в этой точке.dy=A ЕслиА=0,то dy=0.Т.к.А=f’(Xo) то dy=f’(Xo)* ,dy=y’ .полагая y=x:dx=x’ =1* =

Т.е.dx= .Значит dy=f’(Xo)dx, dy=y’dx.Следует:y’=dy/dx;y’=f’(Xo)Отношение диф.ф-ции dy к диф. аргумента dx

ПРОИЗВОДНЫЕ и ДИФ. высших произв. от I порядка y’=f’(x) наз. произв. II поряд:y’’=(y’)’=(f’(x))’=f’’(x)

Пусть ф. y=f(x) диференц. в т.Xo dy=y’dx

Это диффер. I порядка.Диффер. II порядка-дифер. от I порядка и обозн. 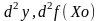т.е.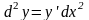 Для высших порядков:

43. :Основные теоремы диференц. Вычисления

ТЕОРЕМА ФЕРМА:Геометр. смысл состоит в том, что если при x=Xo, f приним. найб. знач. на некот. окрестн. т. Xo то касательная к граф. ф-ции параллель. оси OX.Если в т. Xo сущ. конеч. произв., то равна 0.

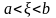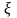ТЕОРЕМА РОЛЛЯ:геометр. смысл состоит в том, что у граф. непрер. на отр. и дифференц. внутри его ф-ции, приним. на его концах одинак. знач., сущ. хотя бы одна точ.,в кот касат. парал. оси OX.Сущ.хотя бы одна точка такая что f’( )=0

ТЕОРЕМА ЛАНГРАНЖА:Если ф-ция непрер. на отр. (a;b). То найдётся точка такая что f(b)-f(a)=f’( )(b-a).

ТЕОРЕМА КОШИ:Пусть ф-ции f(x) и g(x) – непрерыв,дифференц. на интерв.(a:b)Тогда найд. точка . .

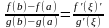Все теоремы наз теорем. о сред. знач.На каждом отр. сущ. хотябы одна точ. для кот. теоремы выполняются