
- •3 Общее уравнение прямой.
- •4. Линии второго порядка
- •4.Эллипс и его каноническое уравнение
- •5.Гипербола
- •6.Парабола
- •7,8,9Понятие матрицы. Линейные операции над матрицами. Произведение матриц. Транспонирование матриц.
- •10. Понятие определителя свойств.
- •11.Способы построения обратной матрицы.
- •17. Решение однородных систем линейных уравнений.
- •21. Прямоугольные декартовы координаты вектора.
- •27. Критерий компланарности трех векторов.
- •34. Монотонные последовательности
- •38. Основные св-ва пределов функций.
- •39. Замечательные пределы
- •II Замечательный предел
- •42. Дифференциал ф-ции и геом.Смысл
- •43. :Основные теоремы диференц. Вычисления
- •45. .Первообразная функция и неопределенный интеграл.
- •50. Опр.Инт. С переем. Верхним пределом.Ф-ла Ньютона-Лейбница
- •53,56. Понятие числового ряда и его сходимость.
27. Критерий компланарности трех векторов.
Утверждение 3. Необходимым и достаточным условием компланарности векторов является равенство нулю их смешанного произведения:
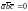 . (1)
. (1)
Доказательство. Если компланарны, то из утверждения 1 получаем , т.е. (1) имеет место.
Пусть
теперь выполняется равенство (1) и
покажем, что векторы
компланарны. Действительно, если бы
векторы
были некомпланарны, то по утверждению
1 их смешанное произведение
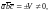 что противоречит (1)
Выражение
смешанного произведения через координаты
перемножаемых векторов.
Пусть векторы
заданы своими координатами:
что противоречит (1)
Выражение
смешанного произведения через координаты
перемножаемых векторов.
Пусть векторы
заданы своими координатами:
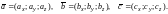 Тогда
Тогда
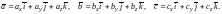
По формуле (8.9) имеем:
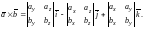
Далее по формуле (7.8) для скалярного произведения получаем:

или
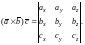 (2)
(2)
Таким образом, смешанное произведение равно определителю третьего порядка, в строках которого стоят соответствующие координаты перемножаемых векторов
32.
Числовая последовательность. Пусть –
множество натуральных чисел. Если
каждому натуральному числу n
поставлено в соответствие некоторое
число
,
то говорят, что определена числовая
последовательность
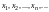 .
Числа
.
Числа
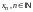 ,
называют элементами
или членами
последовательности.
Числовую последовательность (в дальнейшем
– последовательность) будем еще
записывать
в виде
,
называют элементами
или членами
последовательности.
Числовую последовательность (в дальнейшем
– последовательность) будем еще
записывать
в виде
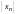 ,
а выражение
называть общим
членом
последовательности,
n
– номером
члена.
,
а выражение
называть общим
членом
последовательности,
n
– номером
члена.
Последовательности
встречались в курсе средней школы.
Например, бесконечная геометрическая
прогрессия 1, q,
 …,
qn,…,
является
числовой последовательностью.
…,
qn,…,
является
числовой последовательностью.
Последовательности
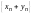 ,
,
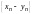 ,
,
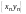 ,
,
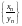 называются соответственно суммой,
разностью, произведением и частным двух
последовательностей {
}
и {
называются соответственно суммой,
разностью, произведением и частным двух
последовательностей {
}
и { }
(для частного
}
(для частного
 ,
,
 ).
).
Простым способом задания последовательности является аналитический способ, т.е. задание с помощью формулы n-го члена:
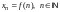 . (1)
. (1)
Формула (1) позволяет определить любой член последовательности по номеру n.
Так, равенства
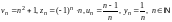
задают соответственно последовательности
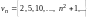 ,
,
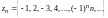 ,
,
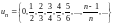 ,
,
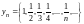 .
.
Последовательность,
у которой все члены принимают равные
между собой значения, называется
постоянной
последовательностью.
Так, например, последовательность с
общим членом
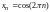 ,
,
имеет вид 1, 1,…, 1,….
,
,
имеет вид 1, 1,…, 1,….
Другой
способ задания числовых последовательностей
– рекуррентный.
Задается начальный элемент x1
(первый член последовательности) и
правило определения n-го
элемента по (n–1)-му:
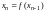 .
Таким образом,
.
Таким образом,
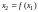 ,
,
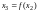 и т.д. При таком способе задания
последовательности для определения
100-го члена надо сначала посчитать 99
предыдущих.
и т.д. При таком способе задания
последовательности для определения
100-го члена надо сначала посчитать 99
предыдущих.
33.
Предел числовой последовательности.
Число a
называется пределом
последовательности
{
},
если
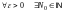 такое, что
такое, что
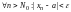 и обозначается
и обозначается
 .
.
Геометрически это означает, что в любой -окрестности точки находятся все члены последовательности, начиная с некоторого номера (зависящего, вообще говоря, от ).
Свойства сходящихся последовательностей.
1.
Для того, чтобы число а
было пределом последовательности
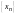 ,
необходимо и достаточно, чтобы
имело вид
,
необходимо и достаточно, чтобы
имело вид
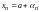 ,
где
,
где
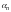 – бесконечно малая последовательность.2.
Сходящаяся
последовательность имеет только один
предел.
– бесконечно малая последовательность.2.
Сходящаяся
последовательность имеет только один
предел.
3. Сходящаяся последовательность ограничена.
4.
Пусть
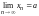 и
и
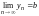 .
.
Тогда: а)
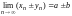 ;
;
б)
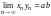 ;
;
в)
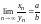 (при условии, что
).
(при условии, что
).
Утверждение
(теорема о двух милиционерах или о
сжатой последовательности).
Пусть даны три последовательности
,
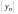 ,
,
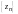 и, начиная с некоторого номера
и, начиная с некоторого номера
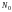 ,
,
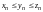 ,
причем последовательности
и
имеют один и тот же предел а.
Тогда последовательность
также имеет предел а.
,
причем последовательности
и
имеют один и тот же предел а.
Тогда последовательность
также имеет предел а.
