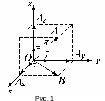
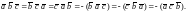- •3 Общее уравнение прямой.
- •4. Линии второго порядка
- •4.Эллипс и его каноническое уравнение
- •5.Гипербола
- •6.Парабола
- •7,8,9Понятие матрицы. Линейные операции над матрицами. Произведение матриц. Транспонирование матриц.
- •10. Понятие определителя свойств.
- •11.Способы построения обратной матрицы.
- •17. Решение однородных систем линейных уравнений.
- •21. Прямоугольные декартовы координаты вектора.
- •27. Критерий компланарности трех векторов.
- •34. Монотонные последовательности
- •38. Основные св-ва пределов функций.
- •39. Замечательные пределы
- •II Замечательный предел
- •42. Дифференциал ф-ции и геом.Смысл
- •43. :Основные теоремы диференц. Вычисления
- •45. .Первообразная функция и неопределенный интеграл.
- •50. Опр.Инт. С переем. Верхним пределом.Ф-ла Ньютона-Лейбница
- •53,56. Понятие числового ряда и его сходимость.
21. Прямоугольные декартовы координаты вектора.
 Рассмотрим
декартову систему координат Охуz.
Пусть
Рассмотрим
декартову систему координат Охуz.
Пусть
 – единичные векторы соответствующих
осей координат Ох,
Оу, Оz,
т.е.
– единичные векторы соответствующих
осей координат Ох,
Оу, Оz,
т.е.
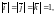 и каждый из них одинаково направлен с
соответствующей осью координат (рис. 1).
Тройка векторов
и каждый из них одинаково направлен с
соответствующей осью координат (рис. 1).
Тройка векторов
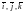 называется базисом.
называется базисом.
Теорема 1. Любой вектор можно единственным образом разложить по базису , т.е. представить в виде
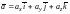 ,
(1)
,
(1)
где
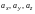 - числа
- числа
22.
Определение скалярного произведения,
его свойства и
механический
смысл.
Скалярным
произведением
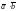 двух ненулевых
векторов
и
называется число, равное произведению
длин векторов на косинус угла между
ними. Если хотя бы один из векторов
и
нулевой, то скалярное произведение
равно нулю.
двух ненулевых
векторов
и
называется число, равное произведению
длин векторов на косинус угла между
ними. Если хотя бы один из векторов
и
нулевой, то скалярное произведение
равно нулю.
Таким образом,
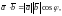 (4)
(4)
где – угол между векторами и (рис. 2).
Скалярное
произведение обозначают символом
,
или
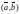 ,
или
,
или
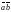 .
.
По
формуле
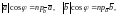 поэтому выражение
(4) можно записать:
поэтому выражение
(4) можно записать:
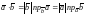 .(5)
.(5)
Для скалярного произведения векторов справедливы следующие свойства:
1)
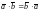 – коммутативность;
– коммутативность;
2)
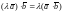 – ассоциативность,
– ассоциативность,
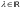 ;
;
3)
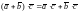 – дистрибутивность;
– дистрибутивность;
4)
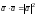 .Доказательство.
Коммутативность скалярного произведения
непосредственно вытекает из формулы
(4).
.Доказательство.
Коммутативность скалярного произведения
непосредственно вытекает из формулы
(4).
Докажем свойство 2). С учетом формул (5) , будем иметь
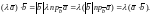 (6)
(6)
Доказательство свойства 3). По формуле (5)
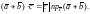 (7)
(7)
Согласно формуле (),
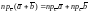 .
.
Таким образом, с учетом (7) и формулы (5), получаем
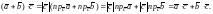
Для
доказательства свойства 4) заметим, что
по формуле (4)
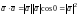 ,
если
,
если
 ,
т.е. если
.
Если же
,
т.е. если
.
Если же
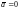 ,
то также, по определению скалярного
произведения,
,
то также, по определению скалярного
произведения,
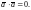 Но, тогда
Но, тогда
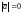 и, поэтому, равенство
в случае
также справедливо. □
и, поэтому, равенство
в случае
также справедливо. □
Скалярное
произведение
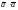 называется скалярным
квадратом
вектора
и обозначается
называется скалярным
квадратом
вектора
и обозначается
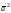 .
На основании свойства 4) имеем:
.
На основании свойства 4) имеем:
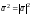 ,
отсюда, в частности,
,
отсюда, в частности,
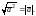
Из свойств 1) и 2) вытекает, что
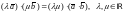 .(8)
.(8)
Из свойства 3) следует, что при скалярном умножении векторных многочленов можно выполнять действия почленно и, в силу (8), объединять коэффициенты векторных сомножителей
23. Перпендикулярности двух векторов. Сформулируем необходимое и достаточное условие перпендикулярности двух векторов.
Свойство 5). Два ненулевых вектора и перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.
Доказательство.
Необходимость. Пусть
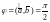 и
и
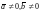 .
Тогда
.
Тогда
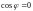
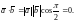
Достаточность.
Пусть
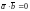 и
и
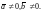 Используя формулу
(4), получаем
Используя формулу
(4), получаем
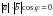 лишь если
или
лишь если
или
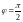 .
Значит,
.
Значит,
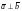 .
□
.
□
Из равенства (4) получаем формулу для определения косинуса угла между ненулевыми векторами:
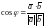 .(9)
.(9)
Отметим,
что из свойств 4) и 5) для базисных векторов
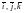 непосредственно получаем следующие
равенства:
непосредственно получаем следующие
равенства:

Выражение
скалярного произведения через координаты
векторов.
Если векторы
и
заданы своими координатами:
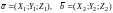 ,
то их скалярное произведение вычисляется
по формуле
,
то их скалярное произведение вычисляется
по формуле
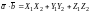 .(11)
.(11)
Доказательство. Разложим векторы и по базису согласно формуле (4):
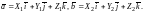
Тогда
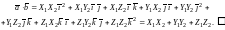 (12)
(12)
Из
формулы (8) и свойства 5) вытекает
необходимое
и достаточное
условие перпендикулярности ненулевых
векторов
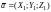 и
и
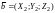 :
сумма произведений одноименных координат
этих векторов равна нулю, т.е.
:
сумма произведений одноименных координат
этих векторов равна нулю, т.е.
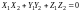 .
.
24.
Ориентация тройки векторов в пространстве.
Тройку
векторов называют
упорядоченной,
если указано, какой из векторов считается
первым, какой вторым и какой третьим. В
записи
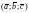 вектор
считается первым,
– вторым,
– третьим; в записи
вектор
считается первым,
– вторым,
– третьим; в записи
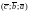 вектор
– первый,
–
второй,
– третий.
вектор
– первый,
–
второй,
– третий.
Упорядоченная тройка некомпланарных векторов называется правой, если после приведения их к общему началу кратчайший поворот от первого ко второму вектору наблюдается с конца третьего вектора против часовой стрелки. В противном случае указанная тройка векторов называется левой.
25.
Векторное произведение двух векторов,
его свойства,
геометрический и физический смысл.
Векторным
произведением
векторов
и
называется вектор
,
длина которого численно равна площади
параллелограмма, построенного на
векторах
и
,
приведенных к общему началу, который
перпендикулярен перемножаемым векторам
и направлен так, что векторы
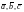 образуют правую тройку
векторов (рис. 1).
образуют правую тройку
векторов (рис. 1).
Рис. 1 |
Рис. 2 |
Если векторы и коллинеарны, то их векторное произведение равно нулевому вектору.
Из определения векторного произведения следует, что (рис.1)
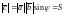 , (1)
, (1)
где – угол между векторами и , S – площадь параллелограмма.
Векторное произведение двух векторов и обозначают символом
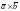 ,
или
,
или
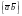 ,
или
,
или
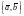 .
.
Выясним
физический
смысл векторного произведения.
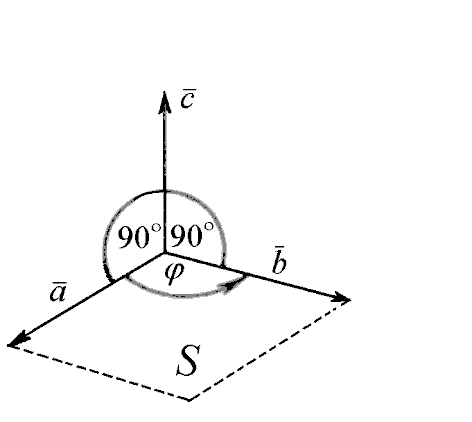
В физике момент силы
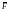 с точкой приложения А
относительно
точки О
изображают вектором
,
перпендикулярным плоскости, в которой
лежат точка О
и вектор
(рис. 2), таким, что тройка векторов
с точкой приложения А
относительно
точки О
изображают вектором
,
перпендикулярным плоскости, в которой
лежат точка О
и вектор
(рис. 2), таким, что тройка векторов
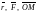 – правая. Длина вектора
определяется как произведение длины
вектора
на плечо
– правая. Длина вектора
определяется как произведение длины
вектора
на плечо
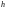 ,
где
– расстояние от точки О
до прямой, на которой лежит вектор силы
,
т.е.
,
где
– расстояние от точки О
до прямой, на которой лежит вектор силы
,
т.е.
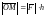 ,
или
,
или
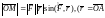 – радиус–вектор точки приложения силы
– радиус–вектор точки приложения силы
 .
Таким образом, момент силы
относительно некоторой точки
,
есть векторное произведение радиус–вектора
.
Таким образом, момент силы
относительно некоторой точки
,
есть векторное произведение радиус–вектора
 точки приложения силы на вектор силы
:
точки приложения силы на вектор силы
:
 .
.
Свойства векторного произведения.
1. При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е.
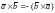 . (2)
. (2)
Доказательство.
Если векторы
и
коллинеарны, то равенство (2) очевидно,
т.к.
и
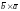 – нулевые векторы.
– нулевые векторы.
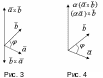 Пусть
и
неколлинеарны. Из определения векторного
произведения вытекает, что векторы
и
имеют одинаковые длины и коллинеарны,
но направлены противоположно (рис. 3),
т.к. векторы
Пусть
и
неколлинеарны. Из определения векторного
произведения вытекает, что векторы
и
имеют одинаковые длины и коллинеарны,
но направлены противоположно (рис. 3),
т.к. векторы
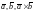 и
и
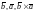 образуют правые тройки. Значит,
.
□
образуют правые тройки. Значит,
.
□
2. Ассоциативность:
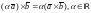 . (3)
. (3)
Для
доказательства равенства (3) используем
следующие рассуждения. Векторы
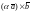 и
и
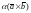 имеют одинаковую длину, т.к. при
получаем
имеют одинаковую длину, т.к. при
получаем

при имеем
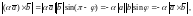
где
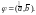 Кроме того, рассматриваемые векторы
одинаково направлены (рис. 4).
Действительно, при
оба имеют то же направление, что и вектор
,
а при
– противоположное. Если
Кроме того, рассматриваемые векторы
одинаково направлены (рис. 4).
Действительно, при
оба имеют то же направление, что и вектор
,
а при
– противоположное. Если
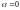 ,
то равенство (3) очевидно
,
то равенство (3) очевидно
26.
Определение смешанного произведения
векторов, его
свойства
и геометрический смысл.
Пусть даны три вектора
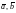 и
.
Умножим
вектор
векторно на
,
а полученный вектор
умножим
скалярно
на
и тем самым определим число
и
.
Умножим
вектор
векторно на
,
а полученный вектор
умножим
скалярно
на
и тем самым определим число
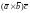 .
Оно называется
векторно-скалярным или смешанным
произведением трех векторов
.
Оно называется
векторно-скалярным или смешанным
произведением трех векторов
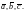 Смешанное произведение
Смешанное произведение
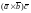 обозначают также
обозначают также
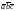 ,
или
,
или
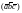 ,
или
,
или
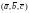 .
.
Выясним геометрический смысл смешанного произведения.
Утверждение1.Смешанное
произведение
равно
объему
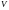 параллелепипеда, построенного на
векторах
,
взятому
со
знаком «+», если тройка
– правая, со знаком «–», если тройка
– левая. Если же
компланарны, то
параллелепипеда, построенного на
векторах
,
взятому
со
знаком «+», если тройка
– правая, со знаком «–», если тройка
– левая. Если же
компланарны, то
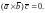
Доказательство.
Пусть даны некомпланарные векторы
,
образующие правую тройку. Обозначим
через
объем параллелепипеда, построенного
на этих векторах; через S
– площадь параллелограмма, построенного
на векторах
и
,
а через h
– высоту параллелепипеда (рис.1). Тогда
из определения векторного и скалярного
произведений получаем
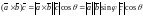 ,
где
– угол между векторами
и
,
а
,
где
– угол между векторами
и
,
а
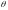 – угол между векторами
и
– угол между векторами
и
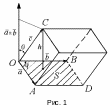 Так
как
Так
как
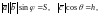 то
то
 Если же тройка
– левая,
то
Если же тройка
– левая,
то
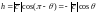 и
и
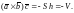
Рассмотрим
теперь случай компланарных векторов
.
Если
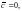 то, очевидно,
Пусть
то, очевидно,
Пусть
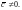 Тогда либо
Тогда либо
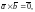 если векторы
и
коллинеарны, либо
если векторы
и
коллинеарны, либо
 если
и
неколлинеарны. В любом случае,
☐
если
и
неколлинеарны. В любом случае,
☐
Из утверждения 1 вытекает, что абсолютная величина остается той же, независимо от порядка сомножителей Что касается знака, то он будет в одних случаях положительным, в других – отрицательным. Это зависит от того, образуют перемножаемые векторы, взятые в указанном порядке, правую или левую тройку.
Таким образом, получаем следующее свойство смешанного произведения.
Утверждение 2. Смешанное произведение не меняется при круговой перестановке его сомножителей; перестановка двух соседних сомножителей меняет знак произведения на противоположный, т.е.