
- •3 Общее уравнение прямой.
- •4. Линии второго порядка
- •4.Эллипс и его каноническое уравнение
- •5.Гипербола
- •6.Парабола
- •7,8,9Понятие матрицы. Линейные операции над матрицами. Произведение матриц. Транспонирование матриц.
- •10. Понятие определителя свойств.
- •11.Способы построения обратной матрицы.
- •17. Решение однородных систем линейных уравнений.
- •21. Прямоугольные декартовы координаты вектора.
- •27. Критерий компланарности трех векторов.
- •34. Монотонные последовательности
- •38. Основные св-ва пределов функций.
- •39. Замечательные пределы
- •II Замечательный предел
- •42. Дифференциал ф-ции и геом.Смысл
- •43. :Основные теоремы диференц. Вычисления
- •45. .Первообразная функция и неопределенный интеграл.
- •50. Опр.Инт. С переем. Верхним пределом.Ф-ла Ньютона-Лейбница
- •53,56. Понятие числового ряда и его сходимость.
5.Гипербола
Гиперболой
называется множество точек плоскости,
модуль разности
расстояний от каждой из которых до
двух заданных точек
и
,
называемых фокусами, есть величина
постоянная, равная
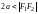 .
.
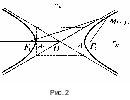
Пусть – расстояние между фокусами и . Выберем декартову систему координат так, чтобы и находились на оси симметрично относительно начала координат (рис. 2).
Если – произвольная точка гиперболы, то, по определению,
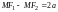 или
или
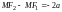 .
.
 Эти
условия можно записать так:
Эти
условия можно записать так:
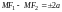 .
.
Отметим,
что
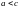 ,
так как из треугольника
,
так как из треугольника
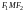 имеем
имеем
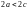 .
.
Рассуждая аналогично, как и при выводе канонического уравнения эллипса, получим каноническое уравнение гиперболы
,
где
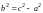 .(
.(
6.Парабола
Параболой называется множество точек плоскости, равноудаленных от данной точки F, называемой фокусом, и от данной прямой L, называемой директрисой.
Для вывода канонического уравнения параболы выберем декартову систему координат Оху так, чтобы ось Ох проходила через фокус F перпендикулярно директрисе, а начало координат О поместим на одинаковых расстояниях от фокуса и директрисы (рис.3).
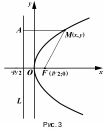 Расстояние
от фокуса до директрисы, называемое
параметром
параболы,
обозначим через р.
Тогда фокус имеет координаты
Расстояние
от фокуса до директрисы, называемое
параметром
параболы,
обозначим через р.
Тогда фокус имеет координаты
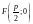 ,
а уравнением директрисы является
,
а уравнением директрисы является
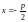 .
.
Пусть М(х;у) – произвольная точка параболы. Тогда, согласно ее определению, имеем
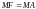 .
(18)
.
(18)
Точка
А
имеет координаты
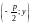 .
Имеем
.
Имеем
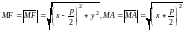 . (19)
. (19)
Из (18) и (19) получаем
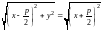 . (20)
. (20)
Отсюда
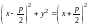 или
или
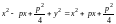 .
Окончательно получаем
.
Окончательно получаем
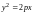 . (21)
. (21)
Уравнение (21) называется каноническим уравнением параболы, изображенной на рис. 3
7,8,9Понятие матрицы. Линейные операции над матрицами. Произведение матриц. Транспонирование матриц.
Понятие матрицы. Прямоугольную таблицу чисел из множества. Матрица -прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество n столбцов.
 (1)
(1)
назовем матрицей. Матрицы обозначаются латинскими буквами A, B, C, D,…
Матрица
A
называется квадратной,
если
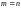 .
В общем случае матрица называется
прямоугольной с размерами
.
В общем случае матрица называется
прямоугольной с размерами
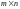 или
прямоугольной матрицей и обозначается
или
прямоугольной матрицей и обозначается
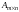 .
Числа
.
Числа
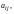
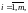
 в (1) называются ее элементами, причем в
записи элемента
в (1) называются ее элементами, причем в
записи элемента
 первый индекс всегда указывает номер
строки, а второй – номер столбца; элементы
первый индекс всегда указывает номер
строки, а второй – номер столбца; элементы
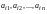 образуют
образуют
 -ую
строку, а элементы
-ую
строку, а элементы
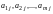 –
–
 -тый
столбец. В связи с этим для обозначения
матрицы (1) будем употреблять запись
-тый
столбец. В связи с этим для обозначения
матрицы (1) будем употреблять запись
 .
Если А
– квадратная матрица порядка n,
то будем писать
.
Если А
– квадратная матрица порядка n,
то будем писать
 .
.
В
математической литературе для записи
матрицы (1) используют также квадратные
скобки
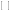 или двойные черты
или двойные черты
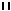 .
.
Матрицы
A
и B
называются равными
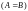 ,
если они имеют одинаковые
размеры и их соответствующие элементы
равны
,
если они имеют одинаковые
размеры и их соответствующие элементы
равны
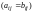 .
.
Прямоугольную матрицу, состоящую из одного столбца
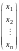 ,
,
называют
столбцовой
(матрицей-столбцом)
и обозначают так:
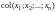 (символ «
(символ «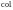 »
в обозначении, если это не создает
недоразумений будем опускать);
прямоугольную матрицу, состоящую из
одной строки
»
в обозначении, если это не создает
недоразумений будем опускать);
прямоугольную матрицу, состоящую из
одной строки
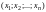 назовем строчной
(матрицей-строкой).
назовем строчной
(матрицей-строкой).
Если все элементы матрицы нулевые, то матрица называется нулевой, ее будем обозначать О. Трапециевидной называют матрицу вида
 .
.
Главной
диагональю
квадратной матрицы называют совокупность
ее элементов
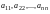 ,
а побочной
диагональю
или просто диагональю
–
,
а побочной
диагональю
или просто диагональю
–
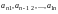 .
Матрица D,
у которой все элементы, расположенные
вне главной диагонали, равны нулю,
.
Матрица D,
у которой все элементы, расположенные
вне главной диагонали, равны нулю,
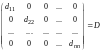
называется
диагональной
и обозначается так:
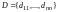 .
.
В
случае
 диагональная матрица называется
единичной и обозначается
диагональная матрица называется
единичной и обозначается
 (или
(или
 ).
).
Если
в квадратной матрице все элементы,
расположенные с одной
стороны от главной диагонали, нули, то
она называется треугольной. При
этом различают верхнюю
треугольную
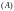 и нижнюю
треугольную
и нижнюю
треугольную
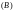 матрицы:
матрицы:
 .
.
Если элементами матрицы являются функции, то ее называют функциональной.
Действия над матрицами.
Суммой
двух матриц
 и
и
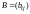 одинаковых
размеров
называется матрица
одинаковых
размеров
называется матрица
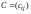 тех же размеров, каждый элемент которой
равен сумме соответствующих элементов
матриц A
и B:
тех же размеров, каждый элемент которой
равен сумме соответствующих элементов
матриц A
и B:
 . (2)
. (2)
Для обозначения суммы матриц A и B используют запись A+B. Операция нахождения суммы данных матриц называется сложением матриц.
Например,
 .
.
Таким образом, можно складывать матрицы только одинаковых размеров.
Из определения сложения матриц и соответствующих свойств сложения действительных чисел вытекает, что эта операция обладает переместительным и сочетательным свойствами:
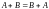 ,
,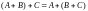 ,
,
где A, B, C – произвольные матрицы одинаковых размеров.
Очевидно, что операцию сложения матриц можно распространить на случай любого числа слагаемых.
Произведением
матрицы
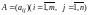 на число
на число
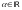 называется
матрица
называется
матрица
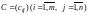 ,
каждый элемент которой
есть произведение соответствующего
элемента матрицы A
и числа
,
каждый элемент которой
есть произведение соответствующего
элемента матрицы A
и числа
 :
:
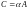 ,
т.е.
,
т.е.
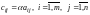 . (3)
. (3)
Операция нахождения произведения матрицы на число называется умножением матрицы на число.
Например,
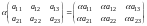 .
.
Из определения (3) произведения матрицы на число вытекают следующие свойства:
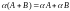 ,
,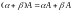 ,
,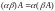 .
.
Здесь
 – матрицы одинаковых размеров, а
– матрицы одинаковых размеров, а
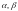 – числа из
– числа из
 .
.
Разностью
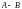 двух матриц
и
одинакового размера
назовем матрицу
такого же размера, которая получается
с помощью правила
двух матриц
и
одинакового размера
назовем матрицу
такого же размера, которая получается
с помощью правила
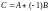 . (4)
. (4)
Из
равенств (4), (3), (2) следует, что каждый
элемент
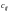 матрицы
есть разность соответствующих элементов
матриц A
и B,
т.е.
матрицы
есть разность соответствующих элементов
матриц A
и B,
т.е.
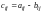 ,
,
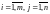 .
.
Произведением двух матриц
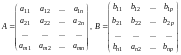
называется матрица
 ,
,
у которой каждый элемент , стоящий на пересечении i-той строки и j-го столбца, равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B:
 ,
,
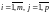 . (5)
. (5)
Таким
образом,
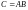 .
Операция нахождения произведения данных
матриц называется умножением
матриц.
.
Операция нахождения произведения данных
матриц называется умножением
матриц.
Например:
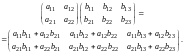
Отметим, что операция умножения двух матриц выполнима тогда и только тогда, когда число столбцов в первом сомножителе равно числу строк во втором.
Используя определение (5), без труда проверяется сочетательное свойство умножения матриц, а также распределительное свойство умножения относительно сложения:
 ,
,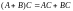 ,
,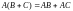 .
.
Операцию умножения матриц можно распространить на случай более двух сомножителей.
Заметим, что умножение AB всегда выполнимо, если сомножители A и B квадратные матрицы одного и того же порядка. Обратим внимание, что умножение матриц не обладает переместительным (коммутативным) свойством. Действительно, например, для матриц

имеем
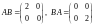 .
.
Если
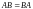 ,
то матрицы
и
называются перестановочными
или коммутирующими
между собой.
,
то матрицы
и
называются перестановочными
или коммутирующими
между собой.
Отметим
также, что диагональная матрица
 ,
у которой все диагональные элементы –
равные числа, т.е.
,
у которой все диагональные элементы –
равные числа, т.е.
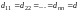 ,
коммутирует с любой квадратной матрицей
,
в частности
,
коммутирует с любой квадратной матрицей
,
в частности
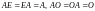 . (6)
. (6)
Из
формулы (6) вытекает, что при умножении
матриц единичная матрица
и нулевая
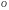 выполняют ту же роль, что числа 1 и 0 при
умножении действительных чисел.
выполняют ту же роль, что числа 1 и 0 при
умножении действительных чисел.
Заметим, что в отличие от чисел, произведение двух ненулевых матриц может дать нулевую матрицу.
Например, в случае
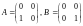
получаем
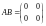 .
.
Введем
еще одну важную операцию над матрицей
– транспонирование
матрицы.
Пусть задана матрица A
размеров
вида (1). После замены строк одноименными
столбцами получим матрицу
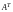 размеров
размеров
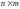 ,
которая называется транспонированной
к заданной:
,
которая называется транспонированной
к заданной:
 .
.
Число строк транспонированной матрицы равно числу столбцов матрицы , а число столбцов – числу строк матрицы .
Операция нахождения матрицы называется транспонированием матрицы, и для нее имеют место следующие свойства:
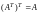 ,
,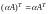 ,
,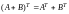 ,
,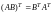 .
.
Если
квадратная матрица
совпадает со своей транспонированной,
т.е.
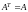 ,
то такая матрица называется симметрической.
,
то такая матрица называется симметрической.
Матрицу
,
для которой
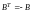 ,
называют кососимметрической.
Легко
видеть, что в кососимметрической матрице
все элементы главной
диагонали нули.
,
называют кососимметрической.
Легко
видеть, что в кососимметрической матрице
все элементы главной
диагонали нули.
Например,
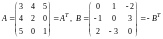 .
.
