Теплоемкость системы численно равна количеству теплоты, которое необходимо сообщить системе, чтобы ее температура увеличилась на 1 Кельвин.
Следовательно, теплоемкость системы C равна C = Q/dT.
Количество теплоты, необходимое для нагревания 1 моля вещества на 1 Кельвин, называется молярной теплоемкостью C = Q/(m/·dT). (14.20)
Количество теплоты, необходимое для нагревания 1 килограмма вещества на 1 Кельвин, называется удельной теплоемкостью c = Q/(m·dT). (14.21)
Молярная теплоемкость легко рассчитать, зная значение удельной теплоемкости и молярную массу
C = с·.
Поскольку количество теплоты, потребляемое системой зависит от вида процесса, то и теплоемкость зависит от вида процесса.
Теплоемкость при постоянном объеме. В зависимости от того, какой параметр системы остается постоянным при протекании процесса, вводят понятие молярной теплоемкости при постоянном объеме и давлении. Запишем первое начало термодинамики для одного моля газа, воспользовавшись определением молярной теплоемкости (14.20) и выражением для расчета элементарной работы (14.4):
C·dT = dU + P·dV. (14.22)
Если газ нагревается при постоянном объеме, то работа, совершаемая им, равняется нулю и сообщаемая извне теплота идет на увеличение внутренней энергии газа. Следовательно, молярная теплоемкость при постоянном объеме Cv равна:
Cv = dU/dT. (14.23)
Молярная теплоемкость при постоянном объеме равна изменению внутренней энергии одного моля газа при его изохорическом нагревании на 1 Кельвин.
Подставив выражение (14.10) в (14.23) получим, что
Cv = i·R/2. (14.24)
Теплоемкость при постоянном давлении. Уравнение Майера. Исходя из определения теплоемкости при постоянном давлении и первого начала термодинамики для изобарического процесса (14.16), можно записать следующее уравнение:
Cp = dU/dT + P·dV/dT. (14.25)
Воспользовавшись уравнением Менделеева-Клапейрона и выражением (14.23), получим, что
Cp = Cv + R. (14.26)
Выражение (14.26) называется уравнением Майера. Оно показывает, что расширение моля идеального газа при постоянном давлении и изменении его температуры на 1 Кельвин требует дополнительного, по сравнению с изобарическим расширением, количества теплоты, необходимого для совершения работы. Это значение равно универсальной газовой постоянной.
Воспользовавшись выражением (14.24), получим
Cp = (i + 2)·R/2. (14.27)
Коэффициент Пуассона Как видно из выражений (14.24) и (14.27) отношение теплоемкостей при постоянном давлении и объеме, называемое коэффициентом Пуассона, определяется только числом степеней свободы атомов или молекул и не зависит явным образом от температуры.
= Cp/Cv = (i + 2)/i. (14.28)
Проблемы классической теории теплоемкости. Молярная теплоемкость газа согласно классической теории не зависит от температуры и равна:
Cv = dU/dT = i·R/2. (14.29)
На самом деле теплоемкость реальных газов зависит от температуры. На рис. 14.3 приведена эта зависимость для водорода. Видно, что существуют области, для которых теплоемкость этого газа не зависит от температуры. При этом сначала число степеней свободы равно 3 (это соответствует наличию только поступательного движения молекул), затем с ростом температуры оно становится равным 5 (к поступательному движению добавляется вращательное), а затем - 7 (добавляется колебательное движение). В промежуточных областях число степеней свободы с классической точки зрения как будто бы изменяется.
Причина несовпадения теории и эксперимента заключается в том, что энергия молекул квантуется, т.е. молекулы могут иметь только строго определенные значения энергии. При этом значения минимальной порции энергии для разных видов движений молекул различны. Если тепловая энергия молекулы много ниже, чем минимальная порция энергии для какого-либо вида движения, то только малая часть молекул способна принять в нем участие. По мере роста температуры постепенно все молекулы вовлекаются в этот процесс. Для водорода сначала все молекулы вовлекаются в поступательное и только малая часть во вращательное и колебательное движение, а затем с ростом температуры становится возможно любое движение молекул.
При достижении температуры диссоциации молекул вся передаваемая водороду теплота идет на распад молекул на атомы (при этом температура газа не изменяется), следовательно, теплоемкость стремиться к бесконечности. Далее с ростом температуры молярная теплоемкость водорода вновь стремиться к значению 3·R/2, характерному для одноатомных молекул.
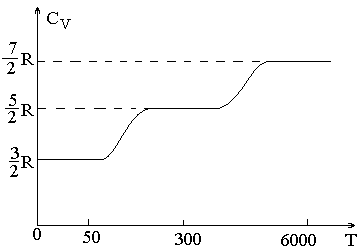Рис.
14.3.