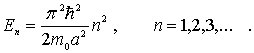- •1. Фотоэффект. Законы фотоэффекта. Уравнение Эйнштейна для фотоэффекта.
- •2. Эффект Комптона.
- •3. Свойства фотонов. Флуктуации интенсивности светового потока.
- •4. Поляризация фотонов. Интерференция фотонов.
- •5. Дифракция рентген-х лучей в кристаллах. Методы исслед дифракции: способы Лауэ, Брэгга и Дебая-Шерера.
- •6. Законы излучения абсолютно черного тела, формула Планка.
- •7. Понятие волн де Бройля. Уравнения де Бройля.
- •8. Эксперименты по волновой природе элементарных частиц.
- •10) Опыты Резерфорда, планетарная модель атома, заряд ядра, распределение зарядов в атоме
- •11) Постулаты Бора, правила квантования: Структура спектральных термов атома водорода, спектральные серии.
- •12. Изотопический сдвиг спектральных линий.
- •13. Квантовомеханические операторы, их свойства, собственные значения и собственные функции.
- •14. Постулаты квантовой механики и описание динамических переменных с помощью операторов.
- •15. Условие одновременной измеримости различных динамических переменных. Соотношение неопределенностей.
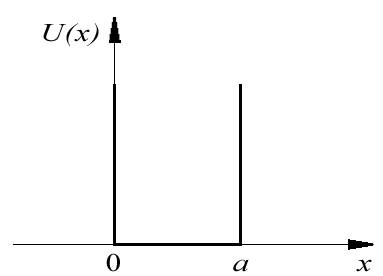
- •16. Частица в одномерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками.
- •19. Магнитные и механические моменты атома, векторная модель атома, гиромагнитное отношение и фактор Ланде
- •Эффект Зеемана.
- •Нормальный эффект Зеемана
- •Эффект Пашена-Бака.
- •22. Эффект Штарка.
- •Электронные конфигурации, принципы заполнения электронных оболочек атомов, правило Хунда.
16. Частица в одномерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками.
Рассмотрим
частицу, находящуюся в одномерной
прямоугольной потенциальной яме с
бесконечно высокими стенками. В этом
случае потенциальная энергия частицы ![]() имеет
вид
имеет
вид
![]()
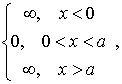
т.е.
внутри ямы (![]() )
потенциальная энергия
)
потенциальная энергия ![]() постоянна
и равна нулю, а вне ямы обращается в
бесконечность ( рис.4.1 ).
постоянна
и равна нулю, а вне ямы обращается в
бесконечность ( рис.4.1 ).
|
Уравнение Шредингера и его решение для частицы в одномерной потенциальной яме с бесконечно высокими стенками^
Уравнение
Шредингера:
![]() ,
где ψ – волновая функция, Е – энергия
частицы.
,
где ψ – волновая функция, Е – энергия
частицы.
Для
случая U
= 0, получим
![]() или
или
![]() ,
где a2
= 2mE/
,
где a2
= 2mE/![]() 2.
Это уравнение описывает положение
частицы внутри потенциальной ямы. Оно
имеет решение, представляющее собой
суперпозицию двух волн, распространяющихся
в противоположных направления вдоль
оси x.
2.
Это уравнение описывает положение
частицы внутри потенциальной ямы. Оно
имеет решение, представляющее собой
суперпозицию двух волн, распространяющихся
в противоположных направления вдоль
оси x.
Итак, соотношение для энергии частицы в бесконечной прямоугольной яме:
|
(4.16) |
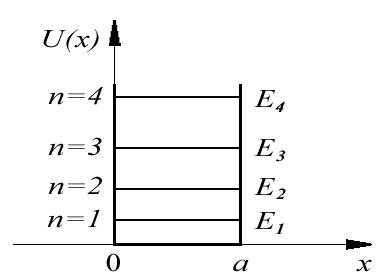
Важной особенностью полученного энергетического спектра (4.16) является его дискретность. Частица, находящаяся в потенциальной яме, может иметь только дискретные, квантованные, значения энергии, определяемые выражением (4.16). Отметим, что решение
|
уравнения Шредингера само по себе к квантованию энергии не приводит, квантование возникает из-за граничных условий, накладываемых на волновую функцию, т.е. из-за равенства нулю волновой функции на границе потенциальной ямы.
Число ![]() в (4.16) ,
определяющее энергию частицы в яме,
называется квантовым
числом,
а соответствующее ему значение
в (4.16) ,
определяющее энергию частицы в яме,
называется квантовым
числом,
а соответствующее ему значение ![]() -
уровнем энергии. Состояние частицы с
наименьшей энергией, в данном случае
с
-
уровнем энергии. Состояние частицы с
наименьшей энергией, в данном случае
с ![]() ,
называется основным
состоянием.
Все остальные состояния являются возбужденными:
значение
,
называется основным
состоянием.
Все остальные состояния являются возбужденными:
значение ![]() отвечает
первому возбужденному состоянию,
значение
отвечает
первому возбужденному состоянию,
значение ![]() -
второму возбужденному состоянию и т.д.
-
второму возбужденному состоянию и т.д.
Следует отметить, что минимальное значение энергии частицы, находящейся в основном состоянии, отлично от нуля. Этот результат согласуется с соотношением неопределенностей и является общим для всех задач квантовой механики. В классической механике минимальную энергию, равную нулю, имеет покоящаяся в яме частица. Такого состояния покоя у квантовой частицы не существует.
19. Магнитные и механические моменты атома, векторная модель атома, гиромагнитное отношение и фактор Ланде
Природа спин-орбитальное взаимодействие – взаимодействие магнитного момента электрона с внутриатомным магнитным полем.
Механический момент электрона:
Орбитальный:
![]()
![]()
Спиновый:
![]()
![]()
Магнитный момент электрона
Орбитальный:
![]()
![]()
Спиновый:
![]()
![]()
Спин – число, характеризующее внутреннюю степень свободы частицы (электрона).
Гиромагнитное отношение -Отношение модуля магнитного момента к модулю механического момента.
Гиромагнитное отношение для орбитального момента:
![]()
Измеряется
в единицах ![]() ,
обозначается gl:
,
обозначается gl:
![]()
Для спинового момента:
![]()
![]()
Фактор Ландэ – гиромагнитное отношение для полного магнитного момента.
![]()
Он связывает магнитный и механический моменты:
![]()
![]()
![]()