Со скольжением в трубе от числа при разных значениях числа Маха.

Она хорошо согласуется с опытными данными Кнудсена и других исследователей. Горизонтальные участки кривых отвечают переходу к свободно-молекулярному течению ( ).

§ 4. Внешнее сопротивление тел в потоке разреженного газа при наличии скольжения

Впервые влияние скольжения на сопротивление тела было обнаружено Милликеном в 1911 г. при исследовании скорости падения мелких масляных капель в воздухе под действием силы тяжести, а также скорости подъема против силы тяжести заряженных капель, находящихся в вертикально направленном электростатическом поле.

Эти исследования Милликена позволили определить гидродинамический эффект скольжения, а также измерить с большой точностью величину заряда электрона.

Мелкие капли, движущиеся с малой скоростью в сплошной среде, имеют форму сферы, сила сопротивления которой при малых значениях числа Рейнольдса , определяется по формуле Стокса

, (30)

где - радиус сферы, - вязкость воздуха, - скорость невозмущенного набегающего потока.

Безразмерный коэффициент сопротивления сферы при

(31)

Опыты, проведенные в интервале и не обнаружили влияния числа Маха и привели к следующей эмпирической формуле:

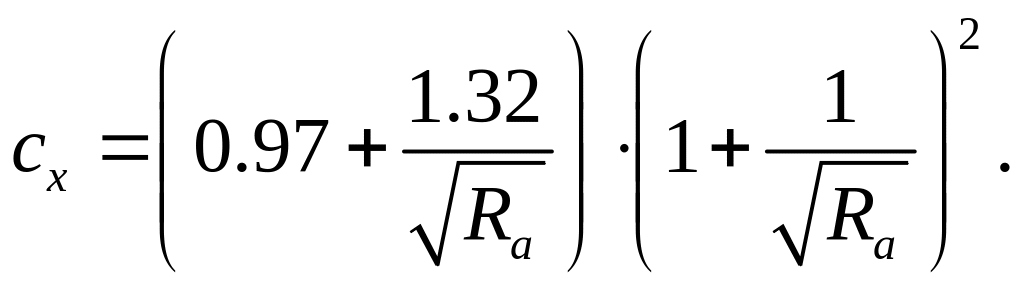(32)

Сопротивление цилиндра при поперечном обтекании его со скольжением рассмотрено Цзяном, который получил следующую теоретическую формулу для коэффициента сопротивления

цилиндра, отнесенного к поперечному сечению (длина цилиндра , радиус ):

(33)

Опытных данных о сопротивлении цилиндра при скольжении в настоящее время нет.

§ 5. Свободно-молекулярные течения газа и элементы кинетической теории газов

Свободно-молекулярный режим течения наблюдается в сильно разреженном газе, когда число Кнудсена значительно больше единицы ( ).

Несмотря на то, что частота столкновений молекул в элементарном объеме при этом режиме пренебрежимо мала, число молекул в единице объема достаточно велико для того, чтобы можно было определять средние макроскопические свойства газа. Например, на высоте 150 км, когда свободный пробег м, число молекул в 1 см³ составляет .

Установим свойства газа, определяющиеся особенностями движения его молекул. Рассмотрим для этого элементарный объем , заполненный большим числом движущихся и изредка сталкивающихся молекул , где - местная концентрация молекул в физическом объеме, т. е. количество молекул в единице объема.

Мгновенные значения проекций скорости , , с отдельных молекул в объеме различаются очень сильно. Можно рассортировать молекулы по скоростям движения, имея в виду, что величины скоростей зависят от координат х, у, z и времени t. Представление о распределении молекул в объеме по скоростям движения дает введенная Максвеллом функция распределения скоростей

,

которая оценивает долю общего числа молекул (в объеме ), обладающих скоростями , , с.

Запишем среднее значение квадрата скорости в полярных координатах

(34)

Параметры и в декартовой и сферической системах координат одинаковы.

На рис. 5. представлено изменение функции в зависимости от для двух значений параметра . Как видно, при некотором значении скорости функция F имеет максимум.

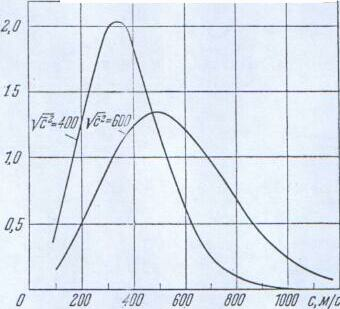
Рис. 5. Функции распределения для