
- •Гиперзвуковые течения газов
- •§ 1. Изменение параметров газа в изоэнтропическом гиперзвуковом потоке
- •§ 2. Гиперзвуковое течение около выпуклого тупого угла
- •Ия потока около выпуклого угла. Ма отклонен
- •§ 3. Плоская ударная волна в гиперзвуковом течении
- •Сферы и цилиндра с конической передней частью от числа Маха.
- •§ 4. Гиперзвуковое обтекание плоской пластины при малом угле атаки
- •§ 5. О гиперзвуковом обтекании тонких заостренных спереди тел
- •Скоростью аффинно-подобных тел.
- •§ 6. Закон сопротивления Ньютона
- •Течения разреженных газов
- •§ 1. Различные типы течений разреженных газов
- •§ 2. Скачки скорости и температуры у стенки при течении газа со скольжением
- •§ 3. Течение газа со скольжением в трубе
- •В трубе.
- •Со скольжением в трубе от числа при разных значениях числа Маха.
- •§ 4. Внешнее сопротивление тел в потоке разреженного газа при наличии скольжения
- •§ 5. Свободно-молекулярные течения газа и элементы кинетической теории газов
- •Двух значений средней квадратичной скорости молекул.
- •Стенкой за единицу времени.
- •§ 6. Давление и напряжение трения при свободно-молекулярном обтекании твердого тела
- •Давления газа на стенку при молекулярном течении.
- •§ 7. Расчет аэродинамических сил при свободно - молекулярном обтекании твердых тел
- •При молекулярном течении газа.
- •§ 8. Свободно-молекулярное течение газа в длинной трубе
- •§ 8. Молекулярное истечение газа через отверстие в стенке и через короткую трубку
Течения разреженных газов
§ 1. Различные типы течений разреженных газов
До сих пор мы рассматривали
газовые течения, в которых газ представлял
собой сплошную среду; это справедливо,
когда длина среднего свободного пробега
молекул газа
![]() весьма мала по сравнению с характерным
размером газового течения
весьма мала по сравнению с характерным
размером газового течения
![]() .
В одних задачах газовой динамики
характерным размером является толщина
пограничного слоя, в других - толщина
или длина обтекаемого тела. Безразмерное
отношение
.
В одних задачах газовой динамики
характерным размером является толщина
пограничного слоя, в других - толщина
или длина обтекаемого тела. Безразмерное
отношение
![]() ,
(1)
,
(1)
определяющее характер среды, называется числом Кнудсена.
При нормальном давлении величина свободного пробега молекул составляет миллионные доли сантиметра. При понижении плотности газа свободный пробег молекул возрастает обратно пропорционально плотности, и если он становится соизмеримым с характерными размерами потока, то дискретная структура газа начинает сказываться на законах газовой динамики и
теплообмена.
Число Кнудсена можно
выразить через известные критерии
подобия - числа Маха М
и Рейнольдса
![]() ;
для этого следует использовать формулу
Чепмена из кинетической теории газов,
;
для этого следует использовать формулу
Чепмена из кинетической теории газов,
связывающую кинематическую
вязкость со свободным пробегом и средней
скоростью движения молекул
![]() :
:
![]() (2)
(2)
Средняя скорость молекул
выражается через скорость звука
![]()
![]() где
где
![]() .
(3)
.
(3)
Тогда из (2) и (3) имеем
![]() (4)
(4)
Подставляя (4) в (1), получаем зависимость числа Кнудсена от отношения числа Маха к числу Рейнольдса
![]() (5)
(5)
Из теории пограничного слоя следует,
что при больших значениях числа Рейнольдса
(![]() )
толщина пограничного слоя
обратно пропорциональна корню квадратному
из числа Рей-
)
толщина пограничного слоя
обратно пропорциональна корню квадратному
из числа Рей-
нольдса
![]()
где х - длина тела. Поэтому
если речь идет о гидродинамическом
трении или теплообмене, когда характерным
размером является толщина пограничного
слоя (![]() ),
то при
),
то при
![]() согласно (5), число Кнудсена становится
пропорциональным отношению числа Маха
к корню квадратному из числа Рейнольдса
согласно (5), число Кнудсена становится
пропорциональным отношению числа Маха
к корню квадратному из числа Рейнольдса
![]() (6)
(6)
При малых значениях числа Рейнольдса
(![]() )
толщина пограничного слоя сравнима с
длиной тела (
)
толщина пограничного слоя сравнима с
длиной тела (![]() ),
поэтому
),
поэтому
![]() (7)
(7)
Имеющиеся теоретические и экспериментальные
данные свидетельствуют о том, что при
очень малых значениях числа Кнудсена
(![]() )
газ ведет себя как сплошная среда. В
интервале значений числа Кнудсена
)
газ ведет себя как сплошная среда. В
интервале значений числа Кнудсена
![]() можно также пользоваться уравнениями
газовой динамики сплошной среды, однако
при этом, как будет показано ниже, следует
в граничные условия на твердой поверхности
вводить поправку на так называемые
«скольжение» и «скачок температуры».
можно также пользоваться уравнениями
газовой динамики сплошной среды, однако
при этом, как будет показано ниже, следует
в граничные условия на твердой поверхности
вводить поправку на так называемые
«скольжение» и «скачок температуры».
При очень больших значениях числа
Кнудсена (![]() )
пограничный слой у поверхности тела не
образуется, так как реэмитированные
(отраженные) поверхностью тела молекулы
сталкиваются с молекулами внешнего
потока на далеком от него расстоянии,
т. е. тело не вносит искажений в поле
скоростей внешнего потока. Для этого
режима «свободно-молекулярного течения
газа», который по имеющимся данным
наблюдается при
)
пограничный слой у поверхности тела не
образуется, так как реэмитированные
(отраженные) поверхностью тела молекулы
сталкиваются с молекулами внешнего
потока на далеком от него расстоянии,
т. е. тело не вносит искажений в поле
скоростей внешнего потока. Для этого
режима «свободно-молекулярного течения
газа», который по имеющимся данным
наблюдается при
![]() ,
трение и теплообмен на поверхности
обтекаемого тела рассчитываются из
условия однократного столкновения
молекул газа с поверхностью.
,
трение и теплообмен на поверхности
обтекаемого тела рассчитываются из
условия однократного столкновения
молекул газа с поверхностью.
Переходная область между режимом со скольжением и свободно-молекулярным режимом остается до сих пор мало изученной, так как в ней приходится учитывать как столкновения молекул между собой, так и неоднократные столкновения их с телом, а это создает большие теоретические трудности.
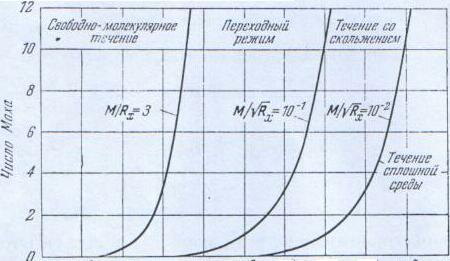
Рис. 1. Границы различных режимов течения разреженного газа.
Таблица 1
Высота Н, км |
0 |
25 |
50 |
75 |
100 |
125 |
150 |
875 |
200 |
Длина свободного пробега , м |
|
|
|
|
|
2,3 |
18 |
80 |
300 |
Сопоставляя данные рис. 1 и таблицы 1, можно получить представление о связи между высотой полета и границами различных режимов.
Для ракеты длиной 3 м влияние скольжения
начинает проявляться с высоты 50 км при
![]() и
30 км при
и
30 км при
![]() .
Свободно-молекулярное течение
устанавливается при любой скорости
полета, начиная с высоты 140 км.
.
Свободно-молекулярное течение
устанавливается при любой скорости
полета, начиная с высоты 140 км.
