§ 4. Гиперзвуковое обтекание плоской пластины при малом угле атаки
Полученные в §§ 2 и 3 выражения дают возможность вывести простые формулы для коэффициентов подъемной силы и лобового сопротивления пластины, обтекаемой газовым потоком большой сверхзвуковой скорости при малом угле атаки.
Коэффициент полной аэродинамической силы, направленной перпендикулярно к пластине, равен
(34)
Здесь уменьшаемое есть безразмерное давление на нижней стороне пластины (за скачком), равное, согласно (28),
Вычитаемое в правой части
равенства (34) представляет собой
безразмерное давление на верхней стороне
пластины (как при обтекании выпуклого
тупого угла), которое на основании (16)
при
имеет вид
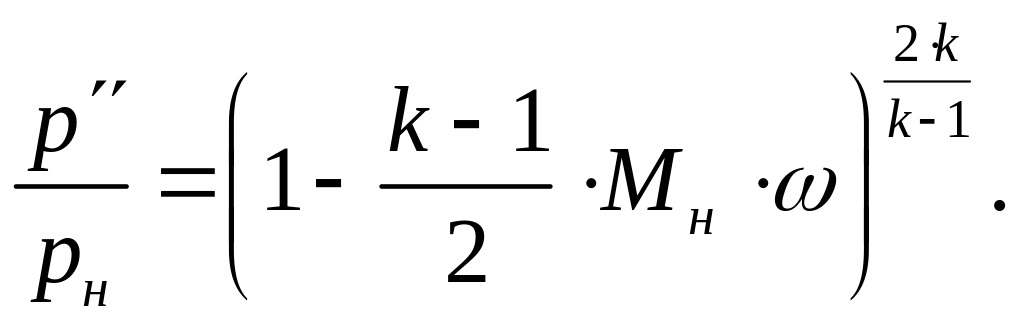
Преобразуя с помощью полученных выражений равенство (34) и используя (32), получим
.
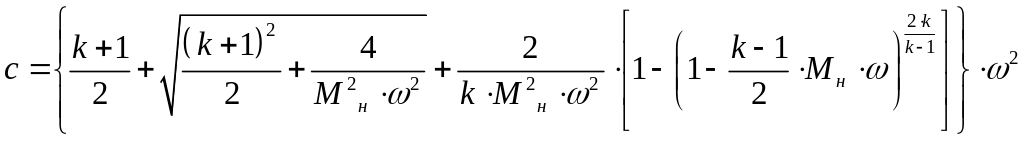(35)
Если угол атаки пластины равен или больше предельного угла поворота потока в течении Прандтля - Майера, который определяется (17), то на верхней стороне пластины устанавливается полный вакуум. В этом случае величина, стоящая в квадратной скобке выражения (35), равна нулю.
При малых углах атаки
коэффициенты подъемной силы
и лобового сопротивления
связаны с коэффициентом полной
аэродинамической силы следующем образом:
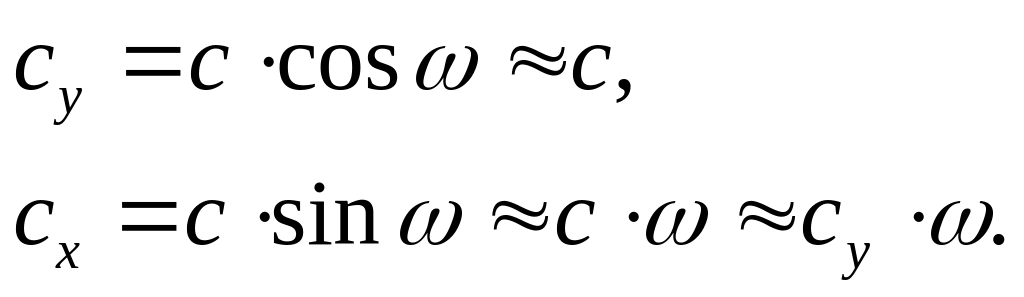(36)
При имеем
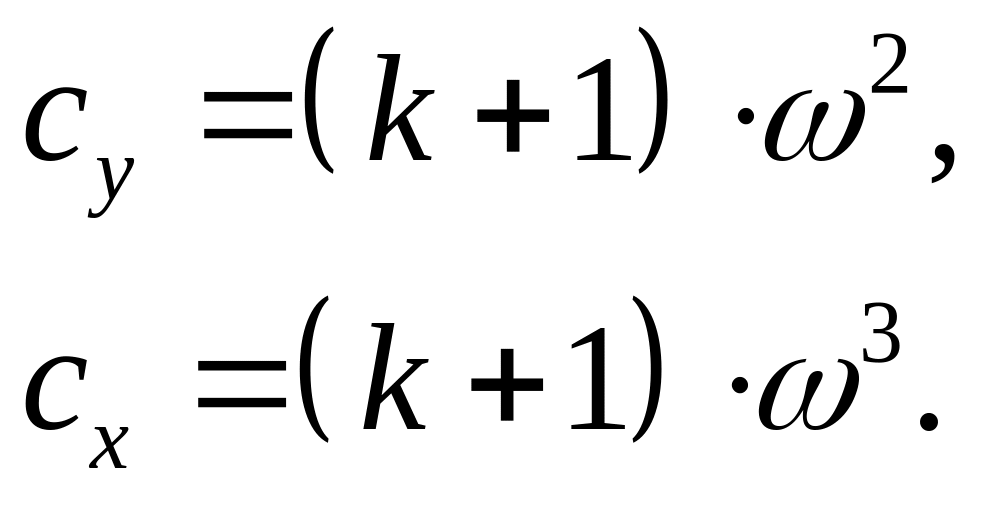
Как видим, аэродинамические
коэффициенты при очень больших значениях
и при малых углах атаки весьма малы и,
кроме того, не зависят от величины
;
в общем случае эти коэффициенты зависят
от критерия
.
§ 5. О гиперзвуковом обтекании тонких заостренных спереди тел
В таких случаях при малых углах заострения тела и малых углах атаки основной критерий
подобия представляет
собой произведения числа Маха набегающего
потока
на некоторый характерный угол
.
Под
может подразумеваться угол отклонения
потока
(угол наклона
поверхности тела к
набегающему потоку) или относительная
толщина тела
(отношение максимального поперечного
размера к длине тела), так как в случае
тонкого тела эти величины пропорциональны.
Тонкие заостренные тела, у которых
критерий
будем в дальнейшем называть
аффинно-подобными. Ясно,
что сохранение
аффинно-подобного обтекания тела при
изменении угла атаки
достигается в том случае, если последний
пропорционален характерному углу тела,
т. е. при условии
.
Итак, относительные величины скоростей,
коэффициенты аэродинамических сил и
другие факторы, характеризующие
гиперзвуковое обтекание тонкого тела,
сохраняют свои значения, если не
изменяются величины
и
.
Это подтверждается опытными
данными, приведенными на рис. 4, на котором
изображены кривые безразмерных значений
избыточного давления на поверхности
цилиндра с оживальной головной частью,
полученные при разных значениях числа
Маха и для различных величин относительной
толщины оживальной части (при нулевом
угле атаки). Как видим кривые распределения
давлений универсальны при
и
,
если выдерживается условие аффинного
подобия:
.
Область действия закона подобия для гиперзвукового обтекания тонкого тела оживальной формы приблизительно определяется следующими границами:
Область применимости
закона подобия значительно расширяется,
если в качестве критерия подобия вместо
величины
взять величину
.
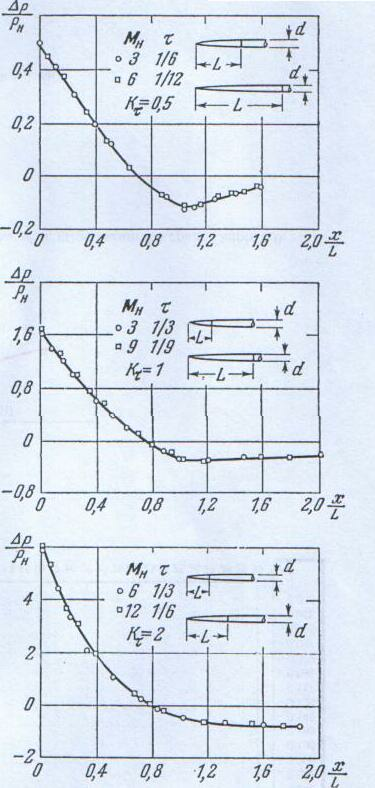
Рис. 4. Распределение давлений при обтекании потоком с большой сверхзвуковой