§ 3. Плоская ударная волна в гиперзвуковом течении
Остановимся теперь на соотношениях, характеризующих плоскую ударную волну, возникающую при обтекании с гиперзвуковой скоростью вогнутого тупого угла. В плоской косой ударной волне изменение плотности будет
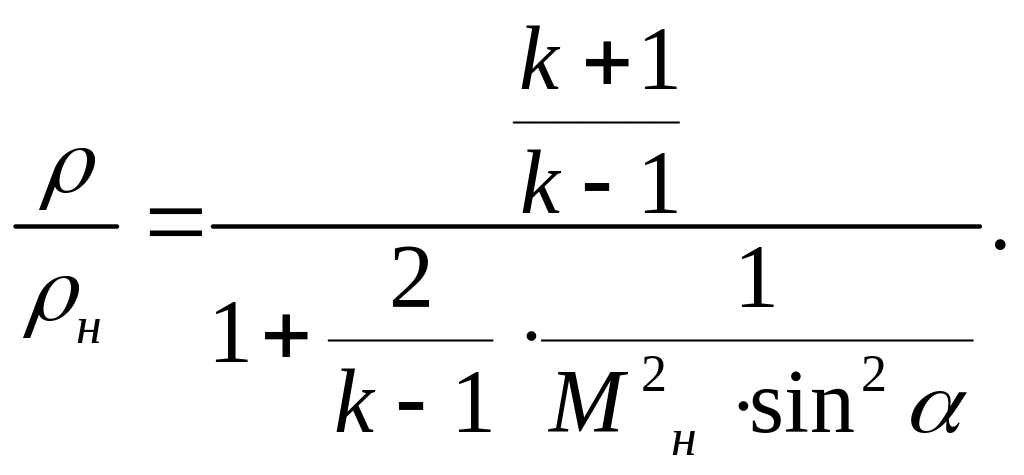(18)
Здесь
- угол наклона фронта ударной волны к
вектору скорости
.
Зависимость угла отклонения потока в ударной волне от угла наклона фронта
.
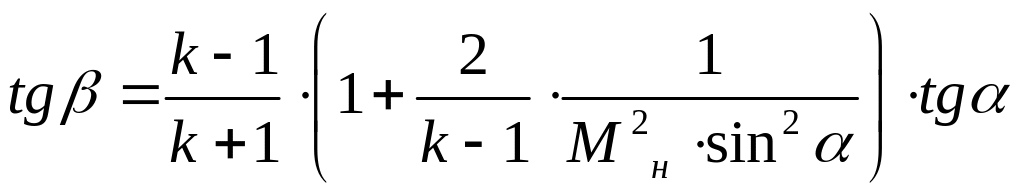(19)
- угол между вектором скорости за
ударной волной и фронтом последней.
Из (18) и (19) с помощью уравнения состояния можно вывести соответствующие зависимости для отношения температур и значений скорости звука в ударной волне.
Возмущения скорости в
ударной волне (
)
найдем из очевидных соотношений
(20)
причем в соответствии со схемой отклонения скоростей в ударной волне (рис. 2) имеем
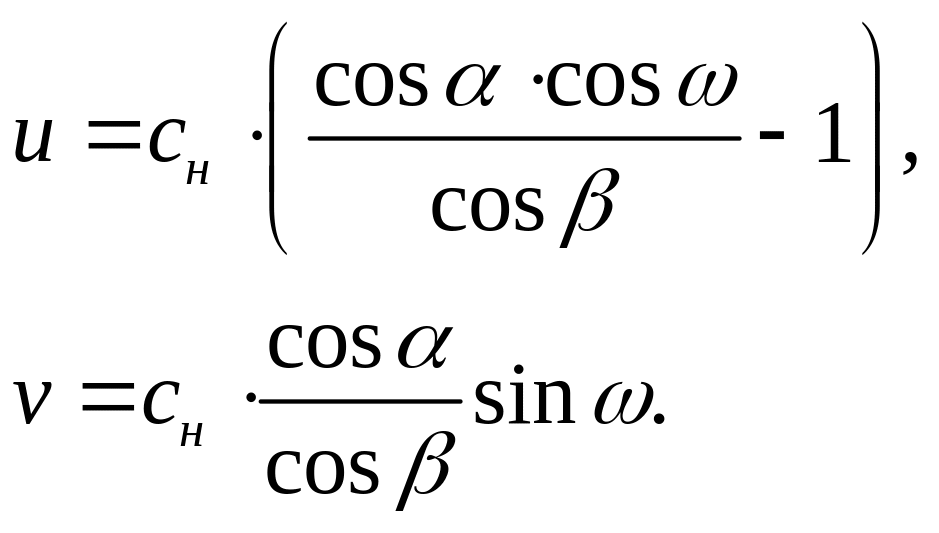(21)
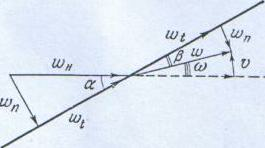
Рис. 2. Схема отклонения потока в ударной волне.
Заменяя
,
после элементарных преобразований
получаем
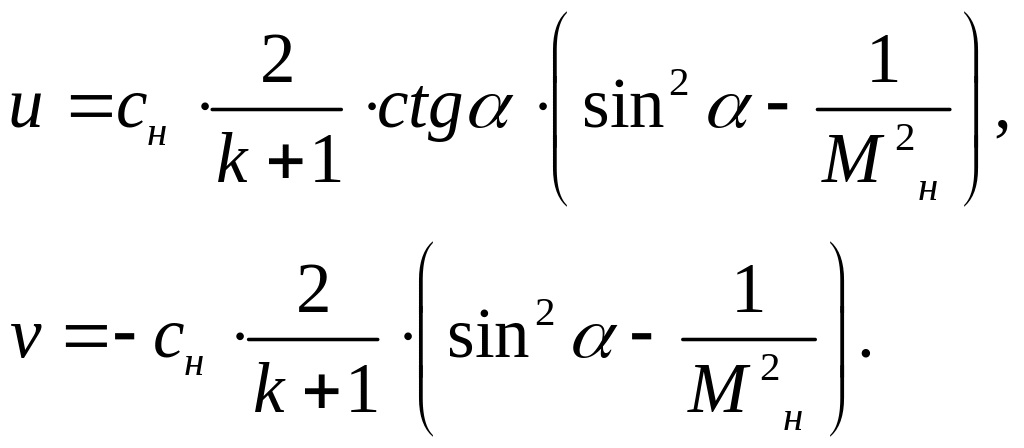(22)
В достаточно интенсивных
скачках уплотнения
(
)
всегда имеет место
неравенство
.
(23)
При любом сколь угодно
малом фиксированном значении угла
отклонения потока
можно достичь такого значения числа
Маха, при котором условие (23) будет
выполнено. Следовательно, в соотношениях
(18)—(22) можно пренебречь членами
и тогда окажется, что безразмерные
значения возмущении скорости
,
,
безразмерная плотность
и угол наклона фронта скачка
не зависят от
,
а безразмерные значения давления
(и температуры
)
пропорциональны величине
:
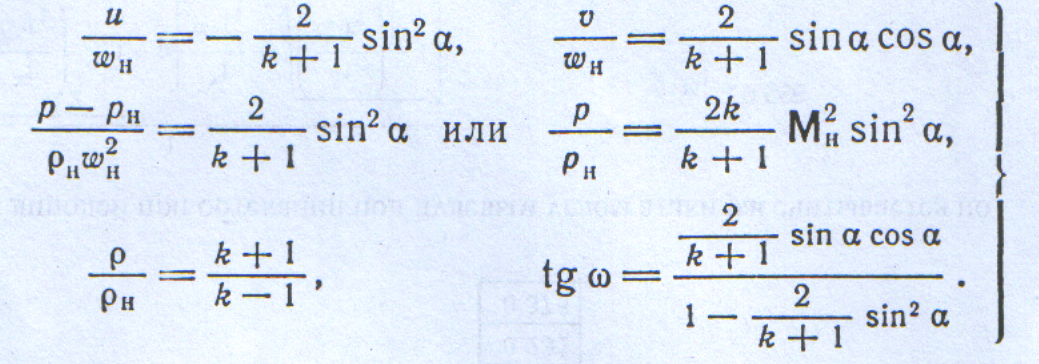(24)
Таким образом, при больших гиперзвуковых скоростях в области за интенсивными скачками уплотнения наблюдается
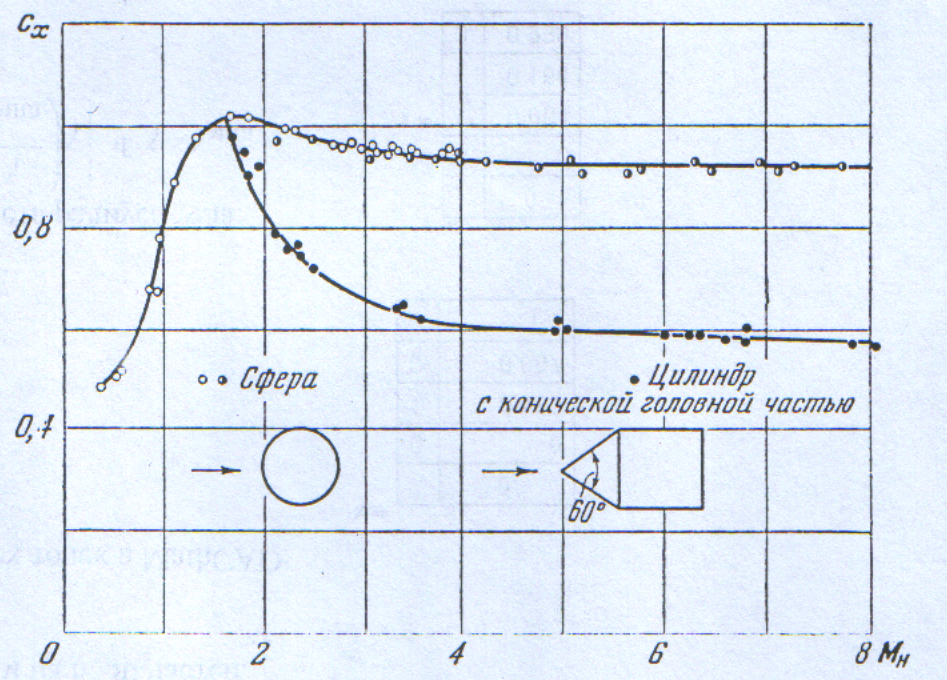
Рис. 3. Зависимость коэффициентов сопротивления
Сферы и цилиндра с конической передней частью от числа Маха.
некоторое предельное
состояние газового течения, при котором
характеризующие его безразмерные
параметры и аэродинамические коэффициенты
не зависят от значения числа
.
Аналогичные особенности газового
течения мы наблюдали при очень
малых—дозвукозых—скоростях
,
когда также свойства потока не зависят
от значения
(несжимаемая жидкость).
Опыты показывают, что
указанное предельное состояние газового
течения (при
)
достигается практически при сравнительно
умеренных значениях числа
.
Об этом свидетельствуют,
например, экспериментальные зависимости
коэффициентов сопротивления
сферы и цилиндра с конической головной
частью, изображенные на
рис. 3; как видим, уже при
значения
весьма близки к
асимптотическим, соответствующим
;
стабильность значений аэродинамических
коэффициентов свидетельствует о
неизменности всей картины течения газа
вблизи тела.
Если ударная волна недостаточно интенсивна, т. е. угол отклонения потока в ней мал, то при гиперзвуковой скорости угол также мал; производим замены
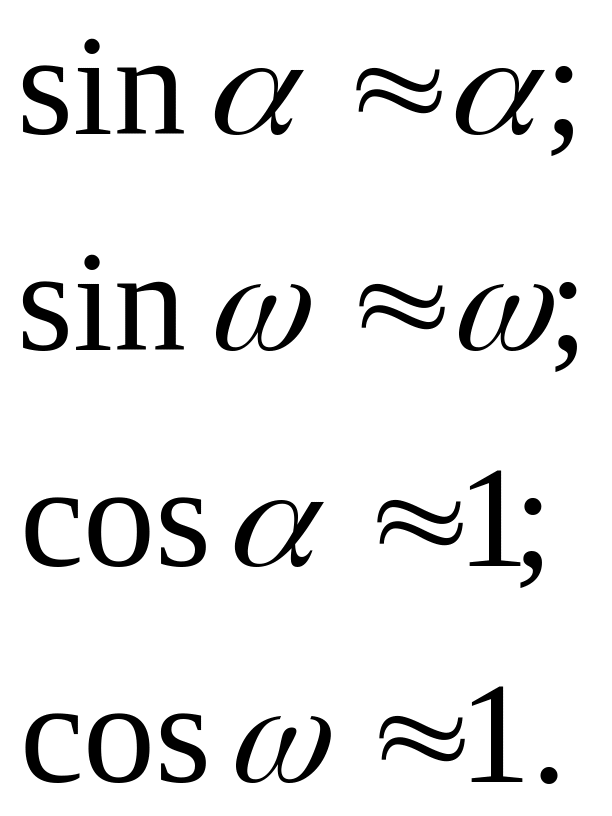
Обозначая
,
получим из (19)
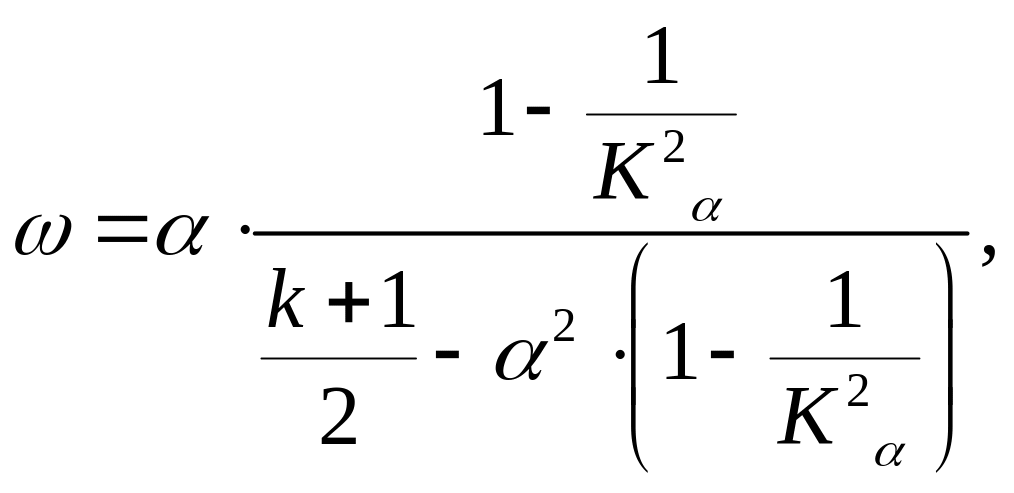(25)
откуда при
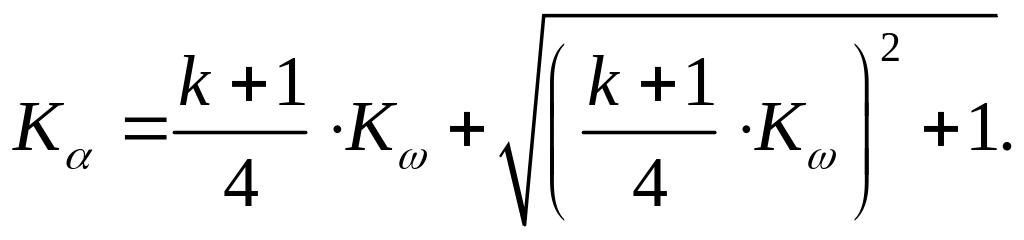(26)
Соответственно из равенства (18)
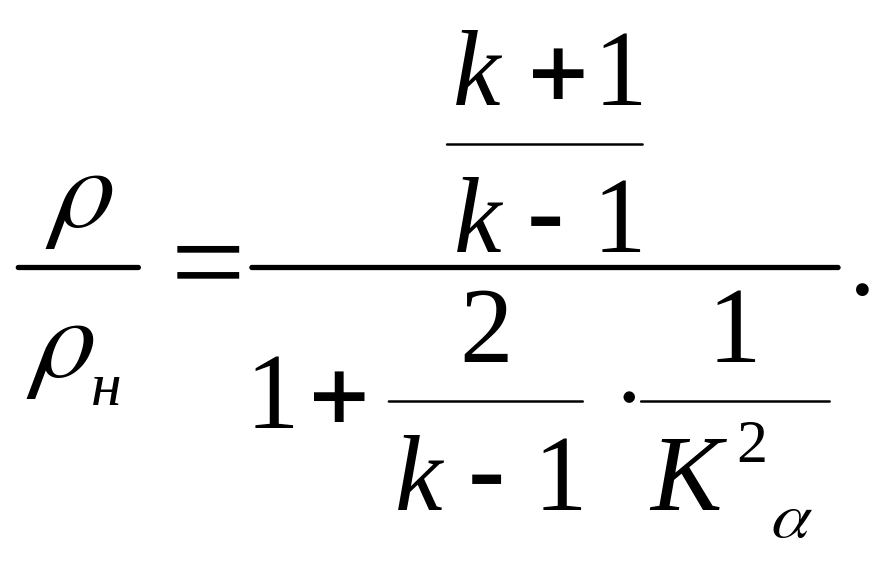(27)
из равенства (19)
,
(28)
из равенства (20)
и
.
(29)
Найдем теперь число Маха за скачком уплотнения
(30)
Как следует из (29), в случае
гиперзвукового течения относительная
скорость газа на скачке при малом угле
последнего почти не изменяется (
).
Тогда из (30)
с помощью (27) и (28) получаем
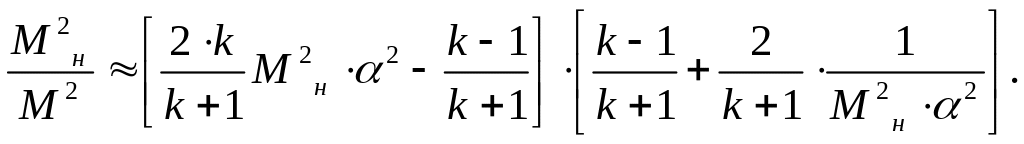(31)
В предельном случае, когда , имеем
При
,
согласно (26),
,
поэтому
Иначе говоря, в случае при малых углах наклона скачка а число Маха за скачком будет очень большим. Если скачок имеет небольшую интенсивность, то числа Маха перед и за скачком при гиперзвуковой скорости имеют значения одного и того же порядка.
При рассмотрении течения Прандтля—Майера (§2) мы представили все параметры в функции угла отклонения потока, тогда как для течения за ударной волной найдены зависимости.
содержащие угол самой ударной волны.
Пользуясь выражениями (25) и (26), получаем
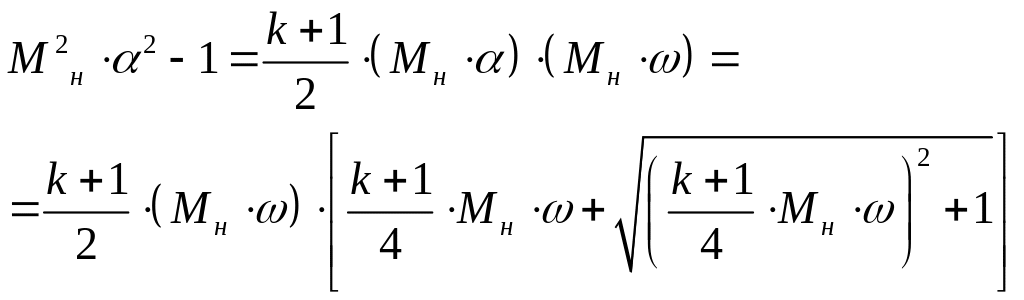(32)
или для сильных возмущений
(
)
.
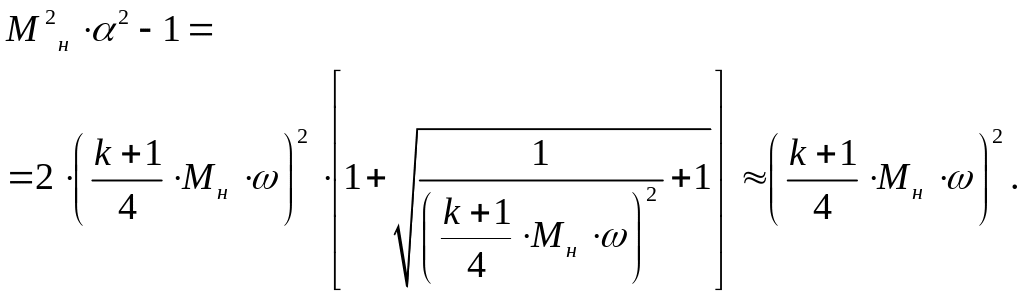(33)
Подставляя (33) в формулы (26)—(27), можно представить изменения давления и плотности в ударной волне, а также величины возмущений скорости в функции угла отклонения потока (угла встречи потока с поверхностью тела).
Из этих зависимостей
следует, что при гиперзвуковых скоростях
в плоской косой ударной волне изменение
параметров определяется (как и в течении
Прандтля—Майера) одним критерием
— произведением числа Маха на угол
отклонения потока.