§ 2. Гиперзвуковое течение около выпуклого тупого угла

Рассмотрим особенности течения с очень большой скоростью около выпуклого тупого угла -гиперзвукового течения Прандтля—Майера (рис. 1). Секундная масса газа между произвольной линией тока и полюсом течения 0 постоянна и может быть вычислена по нормальной к характеристике составляющей скорости, которая равна скорости звука

.

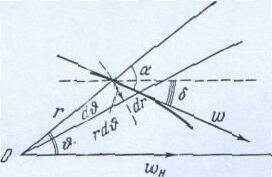
Ия потока около выпуклого угла. Ма отклонен

Рис. 1. Схе

Отсюда после дифференцирования имеем

. (11)

Угол Маха (между линией тока и характеристикой) в случае гиперзвуковой скорости ( ) определяется следующей приближенной зависимостью:

. (12)

Если - угол отклонения потока от первоначального направления, а - угол между заданной характеристикой и первоначальным направлением потока, то очевидно,

, (13)

Здесь принимается во внимание, что направления отсчета углов и противоположны ( > 0, < 0, так как отсчет ведется против часовой стрелки).

Из рис. 1. видно, что

, (14)

так как при , согласно (12),

.

Подставляя (14) в (11), имеем

,

откуда на основании (2), (3) и (5) получаем

.

Интегрируя это уравнение и учитывая соотношения (12) и (13) при условии, что начальному значению отвечает , получаем для гиперзвукового течения следующую связь между числом Маха и углом отклонения потока:

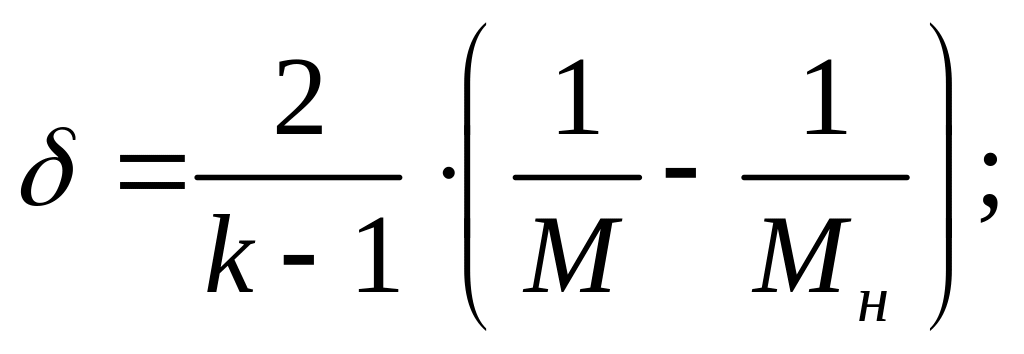(15)

здесь и - текущее и начальное значения числа Маха. Разрешая уравнение (15) относительно текущего значения числа Маха

(15а)

и подставляя это значение в выражения (6)—(10), получим формулы для определения текущих значений давления, плотности, температуры, скорости звука и скорости потока при гиперзвуковом обтекании выпуклого тупого угла.

В частности, для давления имеем

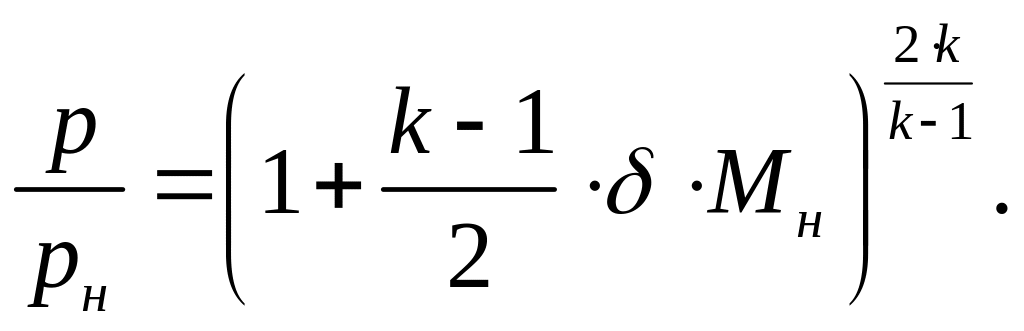(16)

Расчеты показывают, что все полученные таким образом формулы точны при .

Предельный угол отклонения потока соответствует расширению газа до полного вакуума . Тогда из (16) имеем

(17)

Напомним, что при отклонении потока по часовой стрелке угол считается отрицательным ( ).

Как видим, в гиперзвуковом течении около выпуклого угла поперечное возмущение скорости потока по крайней мере на порядок превосходит продольное возмущение ( ). Это значит, что при течении происходит как бы смещение частиц по нормали к направлению невозмущенного потока, величина же продольной скорости практически не изменяется.