§ 8. Свободно-молекулярное течение газа в длинной трубе

Под свободно-молекулярным течением в длинной трубе понимают такое течение, в котором свободный пробег молекул много больше диаметра трубы . В этом случае необходимо учитывать столкновения молекул со стенками, но можно пренебречь столкновениями молекул между собой, следовательно, максвелловское распределение скоростей хаотического движения молекул, устанавливающееся при отражении от стенок, внутри труб не нарушается.

Найдем массу молекул, проходящих в единицу времени через поперечное сечение трубы (рис. 9.). Для этой цели

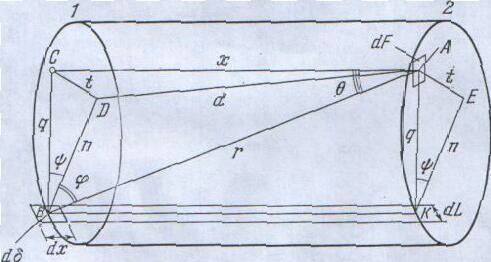
Рис. 9. К определению расхода газа в трубе при молекулярном течении.

вырежем в поперечном сечении 2 трубы элементарную площадку и определим число молекул, отраженных стенками трубы, которое пересечет эту площадку.

Пусть отражающий молекулы элемент поверхности трубы площадью и длиной находится в сечении 1, отстоящем от сечения 2 на расстоянии х, а радиус-вектор ВА, соединяющий

площадки и , имеет длину и составляет угол с осью трубы.

Окончательная формула для секундного расхода газа при свободно-молекулярном течении по длинной круглой трубе имеет следующий вид:

(60)

Отсюда средняя скорость в произвольном сечении трубы

(61)

средняя скорость в начальном сечении трубы

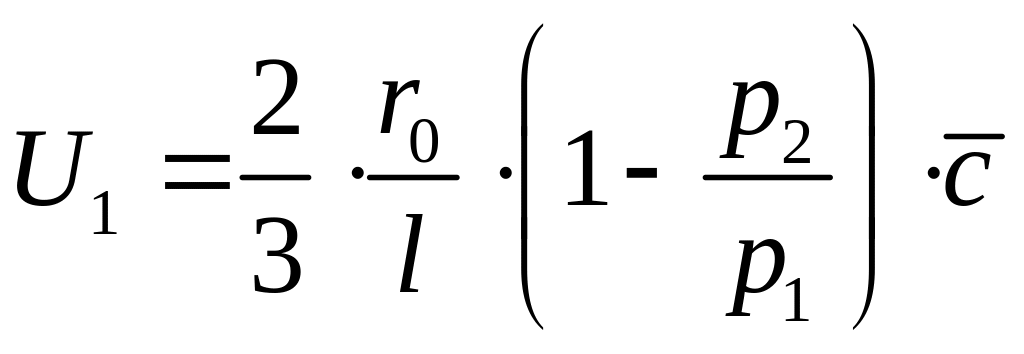(62)

и в конечном сечении трубы

. (63)

Величина - средняя скорость хаотического движения молекул

(64)

Из выражений (61)—(64) видно, что величина средней скорости течения газа при свободно-молекулярном режиме не зависит от плотности (или давления) газа.

Соотношение (133) позволяет найти время, необходимое для заданного понижения давления в сосуде, находящемся под большим разрежением. Например, Кеннард рассчитал, что в колбе объемом в 1 дм³ с начальным давлением 0.01 мм рт. ст. при соединении ее с высоким вакуумом ( ) посредством трубки длиной 30 см и диаметром 2 мм давление понизится вдвое за 3 минуты.

Как видим, откачка газа из сосуда при большом разрежении является весьма медленным процессом.

Однако, если бы течение в трубке в указанном примере Кеннарда происходило по закону Пуазейля (как для сплошной среды), то для снижения давления в колбе вдвое понадобилось бы не 3 минуты, а 2 часа.

§ 8. Молекулярное истечение газа через отверстие в стенке и через короткую трубку

Рассмотрим свободно-молекулярное перетекание газа через отверстие радиуса в стенке (рис. 10.), по обе стороны которой даьлспи/;, температуры и илотноии ггиа исодииакииы.

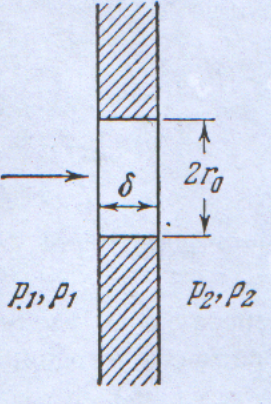
Рис. 10. К расчету молекулярного истечения через отверстие в стенке.

Пусть толщина стенки сравнима с длиной свободного пробега молекул, вследствие чего возможно лишь однократное столкновение молекулы с внутренней поверхностью, ограничивающей отверстие.

Секундная масса молекул, попадающая в отверстие из зоны 1 в зону 2, согласно (45) составляет

Секундная масса молекул, которые ударяются о внутреннюю поверхность отверстия, приблизительно равна

Последнее выражение не является точным, так как состояния газа внутри отверстия и в зоне отличаются. Около половины массы приходит из зоны 1 и после отражения от стенки делится на две равные части, из которых одна отражается в зону 1; в итоге из зоны 1 вытекает в отверстие секундная масса

(65)

Аналогичным образом определяется масса, вытекающая в отверстие из зоны 2:

(66)

Суммарный расход газа, устанавливающийся в направлении к зоне 2, в которой величина имеет меньшее значение, очевидно, равен

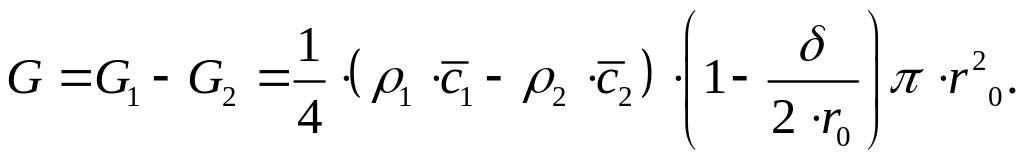(67)

или на основании уравнения состояния и соотношений (3)

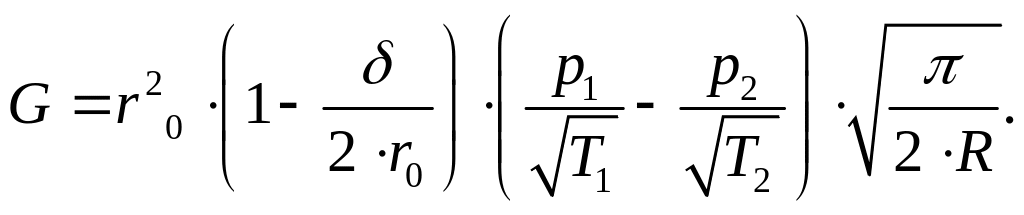(68)

Из формулы (68) следует, что молекулярное истечение возможно даже в сторону более высокого давления (если корень квадратный из температуры увеличивается сильнее, чем давления); при равных давлениях истечение происходит в сторону более высокой температуры (термодиффузия); равновесие (нулевой расход) устанавливается при условии

(69)