Давления газа на стенку при молекулярном течении.

Полное число, молекул , ударяющихся о единичный элемент площади равно

. (43)

Секундный поток массы молекул, падающих на единичную площадку поверхности тела:

(44)

Для неподвижного газа ( ) имеем

(45)

Определяя аэродинамические силы, которые возникают на единичной площадке тела при свободно-молекулярном обтекании, следует иметь в виду, что проекция аэродинамической силы равна разности проекций на ту же ось количеств движения секундной массы молекул, падающих на площадку и отраженных от нее.

Окончательное выражение для давления, которое оказывает свободно-молекулярное течение газа на элемент поверхности, ориентированный по нормали к составляющей скорости невозмущенного

потока газа:

(46)

Аналогичным образом получаем общую формулу для напряжения трения на элементе поверхности

при свободно-молекулярном течении

(47)

В частном случае невозмущенного потока, перпендикулярного к поверхности тела ( ), касательное напряжение (трение) равно нулю

(48)

В частном случае потока, параллельного поверхности тела ( ), давление

(49)

и напряжение трения

(50)

При полностью диффузном отражении молекул от стенки ( ) имеем

(51)

§ 7. Расчет аэродинамических сил при свободно - молекулярном обтекании твердых тел

В предыдущем параграфе указаны методы определения нормальных и тангенциальных напряжений, возникающих на элементарной площадке поверхности тела при свободно-молекулярном обтекании.

Найдем аэродинамические силы, действующие на тело в целом.

Пусть вектор скорости невозмущенного потока составляет угол с элементом поверхности тела (местный угол атаки), тогда угол между вектором и нормалью к поверхности (рис. 8.).

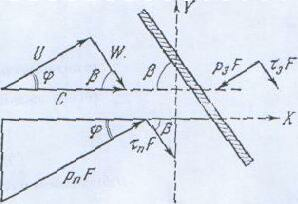
Рис. 8. К определению аэродинамических сил на пластине

При молекулярном течении газа.

Следовательно, проекции скорости на нормаль и касательную к поверхности составляют соответственно

(52)

Определим силы, действующие на пластину. Нормальная к пластине составляющая аэродинамической силы равна произведению площади пластины на разность давлений, приложенных к передней и задней ее сторонам

(53)

Тангенциальная сила равна произведению площади пластины на сумму напряжений трения, возникающих на обеих ее сторонах:

(54)

Теперь нетрудно определить суммарную аэродинамическую силу, направленную перпендикулярно к скорости набегающего потока, т. е. подъемную силу на пластине

(55)

и суммарную аэродинамическую силу, направленную по скорости набегающего потока, т. е. силу сопротивления пластины

(56)

Найдем из (55) и (56) аэродинамические коэффициенты пластины при свободно - молекулярном обтекании

(57)

(58)

Коэффициенты и можно выразить в функции числа Маха, если с помощью (35) и (39) вероятную скорость хаотического движения молекул заменить скоростью звука. В соответствии с этим имеем

(59)